python/TangDou/AcWing_TiGao/T5/OuLaHanShu/201.md

##AcWing 201. 可见的点

一、题目描述

在一个平面直角坐标系的第一象限内，如果一个点 (x,y) 与原点 (0,0) 的连线中没有通过其他任何点，则称 该点在原点处是可见的 。

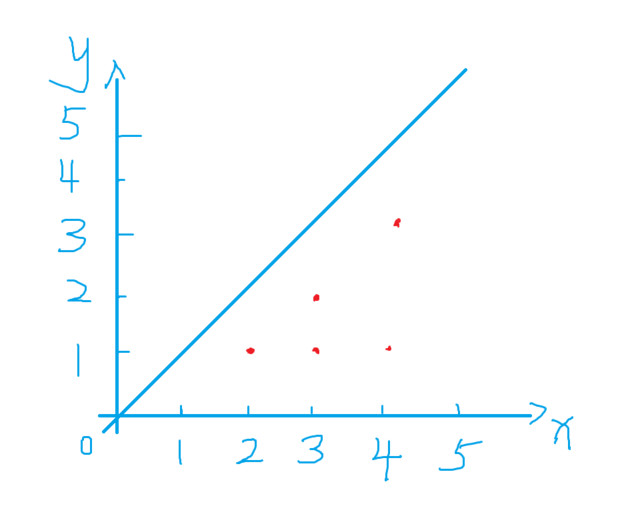
例如，点 (4,2) 就是不可见的，因为它与原点的连线会通过点 (2,1)。

部分可见点与原点的连线如下图所示：

编写一个程序，计算给定整数 N 的情况下，满足 0≤x，y≤N 的可见点 (x，y) 的数量（可见点不包括原点）。

输入格式 第一行包含整数 C，表示共有 C 组测试数据。 每组测试数据占一行，包含一个整数 N。

输出格式 每组测试数据的输出占据一行。

应包括：测试数据的编号（从 1 开始），该组测试数据对应的 N 以及可见点的数量。

同行数据之间用空格隔开。

数据范围 1≤N,C≤1000

输入样例：

4
2
4
5
231

输出样例：

1 2 5
2 4 13
3 5 21
4 231 32549

二、前导知识

欧拉函数专题

三、算法分析

设(x_0,y_0)是某一直线射到的 第一个点，则该方程为y=kx,其中k=\frac{y_0}{x_0}，该直线有以下性质：

• ① 直线方程上的其他点均是(x_0,y_0)的倍数，即(m\cdot x_0,m\cdot y_0),因为斜率相同嘛

• ② \frac{x_0}{y_0}=1:

  • 此情况 特殊，只有一个点满足，就是(1,1)

• ③ \frac{x_0}{y_0} \neq 1时，两者必然互质:

  • 证明：如果不互质，并且斜率一样，那么它前面的互质点对，必然把它挡上。

求(x,y)互质的点对数量，就是本题的题意。

gcd(x,y)=1，联想到 欧拉函数 。

欧拉函数求的是1 \sim n 中与 n 互质的数的个数，若需要使用欧拉函数，与n互质的数需要小于等于它本身，因此求0 <= x ,y <= n中，(x,y)互质的个数需要进行分类，使得某一边小于等于另一边，如图所示，对y = x直线进行切割，使得两边的点对称，只需求右下方区域即可，右下区域的点满足x > y的性质，且y 属于1到x - 1的区间，因此对于每个x，求出1到x - 1中与x互质的数的个数，即相当于求x的欧拉函数,因此 用筛法求出1到x的所有欧拉函数。

注： ① 这里说的x>y是指离散的整数点 ② 最大是n,同时也要考虑每个小于n的数字的欧拉函数值 即 sum=2*(phi(2)+phi(3)+...+phi(n))+1

由于2到n中的欧拉函数的个数需要算两次(对称)，而x=y=1时只需要算一次，因此\displaystyle res=1 +2*\sum_{i=2}^{n}phi(i)

时间复杂度

线性筛法求欧拉函数，所以是O(n)的。

四、暴力实现

因为本题数据量并不大，也可以不用筛法，直接暴力O(n^2)进行计算每个数字的欧拉函数，也是可以的，但考虑到通用性，还是 建议用筛法求欧拉函数。

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;

// 欧拉函数
int phi(int x) {
    int res = x;
    for (int i = 2; i * i <= x; i++) // 从2枚举到sqrt(x)
        if (x % i == 0) {            // 如果i是x的小因子
            res = res / i * (i - 1);
            while (x % i == 0) x /= i; //
        }
    if (x > 1) res = res / x * (x - 1);
    return res;
}

int main() {
    int n, m;
    cin >> m;
    for (int i = 1; i <= m; i++) {
        cin >> n;
        int res = 1;                                    // x=y 记1个
        for (int j = 1; j <= n; j++) res += phi(j) * 2; // 叠加两倍的欧拉函数值
        printf("%d %d %d\n", i, n, res);
    }
    return 0;
}

五、筛法实现

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;

// 筛法求欧拉函数
int primes[N], cnt;
bool st[N];
int phi[N];
void euler(int n) {
    phi[1] = 1;
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; primes[j] * i <= n; j++) {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) {
                phi[i * primes[j]] = phi[i] * primes[j];
                break;
            }
            phi[i * primes[j]] = phi[i] * (primes[j] - 1);
        }
    }
}

int main() {
    // 利用筛法，预处理出欧拉函数值数组
    euler(N - 1); // 这里注意一下是N-1,防止数组越界

    int n, m;
    cin >> m;
    for (int i = 1; i <= m; i++) {
        cin >> n;
        int res = 1;                                    // x=y 记1个
        for (int j = 1; j <= n; j++) res += phi[j] * 2; // 叠加两倍的欧拉函数值
        printf("%d %d %d\n", i, n, res);
    }

    return 0;
}

前缀和优化一下：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
const int N = 1010;

// 筛法求欧拉函数
int primes[N], cnt;
bool st[N];
int phi[N];
int s[N];
void euler(int n) {
    phi[1] = 1;
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; primes[j] * i <= n; j++) {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) {
                phi[i * primes[j]] = phi[i] * primes[j];
                break;
            }
            phi[i * primes[j]] = phi[i] * (primes[j] - 1);
        }
    }
}

signed main() {
    // 利用筛法，预处理出欧拉函数值数组
    euler(N - 1); // 这里注意一下是N-1,防止数组越界

    // 前缀和优化版本
    for (int i = 1; i < N; i++) s[i] = s[i - 1] + phi[i];

    int n, m;
    cin >> m;
    for (int i = 1; i <= m; i++) {
        cin >> n;
        printf("%d %d %d\n", i, n, s[n] * 2 + 1);
    }
    return 0;
}