python/TangDou/AcWing_TiGao/T4/1250.md

##AcWing 1250. 格子游戏

一、题目描述

Alice和Bob玩了一个古老的游戏：首先画一个 n×n 的点阵（下图 n=3 ）。

接着，他们两个轮流在相邻的点之间画上红边和蓝边：

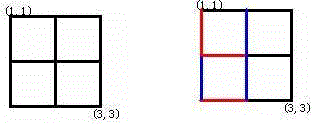
直到围成一个封闭的圈（面积不必为 1）为止，“封圈”的那个人就是赢家。因为棋盘实在是太大了，他们的游戏实在是太长了！

他们甚至在游戏中都不知道谁赢得了游戏。

于是请你写一个程序，帮助他们计算他们是否结束了游戏？

输入格式 输入数据第一行为两个整数 n 和 m。n表示点阵的大小，m 表示一共画了 m 条线。

以后 m 行，每行首先有两个数字 (x,y)，代表了画线的起点坐标，接着用空格隔开一个字符，假如字符是 D，则是向下连一条边，如果是 R 就是向右连一条边。

输入数据不会有重复的边且保证正确。

输出格式 输出一行：在第几步的时候结束。

假如 m 步之后也没有结束，则输出一行“draw”。

数据范围 $1≤n≤200， 1≤m≤24000$

输入样例：

3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D

输出样例：

4

二、解题思路

判断是否成环,可以判断他们没连接前,他们的祖宗结点是否一致，如果一致,连接起来就必然成环。

三、实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 200 * 200 + 10;

int n, m;
int p[N];

// 二维转一维的办法,坐标从(1,1)开始
int get(int x, int y) {
    return (x - 1) * n + y;
}

// 最简并查集
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]); // 路径压缩
    return p[x];
}
int main() {
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n * n; i++) p[i] = i; // 并查集初始化

    int res = 0;
    for (int i = 1; i <= m; i++) {
        int x, y;
        char d;
        cin >> x >> y >> d;
        int a = get(x, y); // 计算a点点号
        int b;
        if (d == 'D') // 向下走
            b = get(x + 1, y);
        else // 向右走
            b = get(x, y + 1);

        // a,b需要两次相遇，才是出现了环~
        int pa = find(a), pb = find(b);
        if (pa == pb) {
            res = i; // 记录操作步数
            break;
        }
        // 合并并查集
        p[pa] = pb;
    }

    if (!res)         // 没有修改过这个值
        puts("draw"); // 平局
    else              // 输出操作步数
        printf("%d\n", res);
    return 0;
}