python/TangDou/AcWing_TiGao/T3/MinialSpanningTree/1141.md

AcWing 1141 局域网

一、题目描述

某个局域网内有 n 台计算机和 k 条 双向 网线，计算机的编号是 1∼n。由于搭建局域网时工作人员的疏忽，现在局域网内的连接形成了回路，我们知道如果局域网形成回路那么数据将不停的在回路内传输，造成网络卡的现象。

注意：

对于某一个连接，虽然它是双向的，但我们不将其当做回路。本题中所描述的回路至少要包含两条不同的连接。

两台计算机之间最多只会存在一条连接。(无重边)

不存在一条连接，它所连接的两端是同一台计算机。(无环)

因为连接计算机的网线本身不同，所以有一些连线不是很畅通，我们用 f(i,j) 表示 i,j 之间连接的畅通程度，f(i,j) 值 越小 表示 i,j 之间连接 越通畅。

现在我们需要解决回路问题，我们将除去一些连线，使得网络中 没有回路 且 不影响连通性（即如果之前某两个点是连通的，去完之后也必须是连通的），并且被除去网线的 \sum f(i,j) 最大，请求出这个 最大值。

输入格式 第一行两个正整数 n,k。

接下来的 k 行每行三个正整数 i,j,m 表示 i,j 两台计算机之间有网线联通，通畅程度为 m。

输出格式 一个正整数，表示被除去网线的 \sum f(i,j) 的最大值。

数据范围 1≤n≤100 ,0≤k≤200,1≤f(i,j)≤1000

输入样例：

5 5
1 2 8
1 3 1
1 5 3
2 4 5
3 4 2

输出样例：

8

二、Kruskal算法

本题要求 被除去网线的通畅程度之和最大，则要求 留下来的网线通畅程度最小，也就是求图的 最小生成树， 由于原图 不一定是连通图，所以要求的实际上是原图的 最小生成森林，即若干个生成树的集合。

kruskal算法是 求连通块 的，所以这个题直接用 kruskal 很容易求出来。

if (cnt < n - 1) res = INF;

这句话需要注释掉，比如下面的数据用例：

6 6
1 2 5
1 3 4
2 3 8
4 5 7
4 6 2
5 6 1

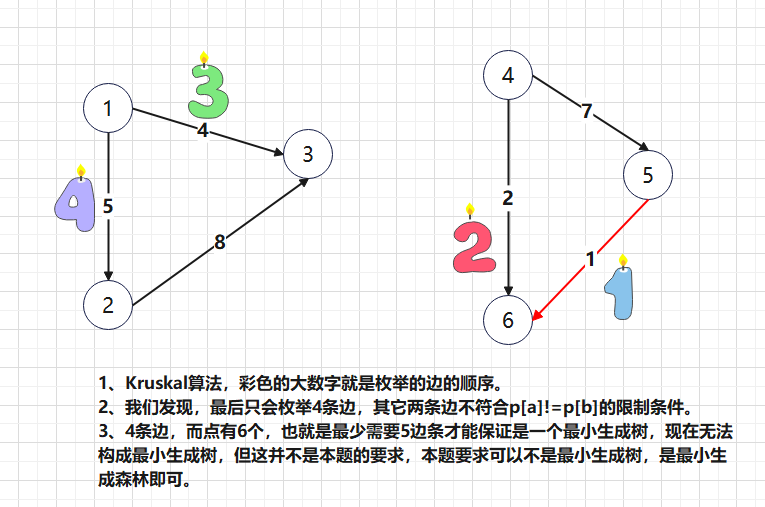
我们发现，1,2,3是一伙，4,5,6是另一伙，这两个家庭不通！如果按照模板的意思，那么就没有最小生成树！

#include <bits/stdc++.h>
using namespace std;
const int N = 110, M = 210;
const int INF = 0x3f3f3f3f;

int n, m; // n条顶点,m条边
int res;  // 最小生成树的权值和
int cnt;  // 最小生成树的结点数

// Kruskal用到的结构体
struct Node {
    int a, b, c;
    bool const operator<(const Node &t) const {
        return c < t.c; // 边权小的在前
    }
} edge[M]; // 数组长度为是边数

// 并查集
int p[N];
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

// Kruskal算法
void kruskal() {
    // 1、按边权由小到大排序
    sort(edge, edge + m);
    // 2、并查集初始化
    for (int i = 1; i <= n; i++) p[i] = i;
    // 3、迭代m次
    for (int i = 0; i < m; i++) {
        int a = edge[i].a, b = edge[i].b, c = edge[i].c;
        a = find(a), b = find(b);
        if (a != b)
            p[a] = b, res += c, cnt++; // cnt是指已经连接上边的数量
    }
    // 这句话需要注释掉，原因如下：
    /*
    6 6
    1 2 5
    1 3 4
    2 3 8
    4 5 7
    4 6 2
    5 6 1
    我们发现，1,2,3是一伙，4,5,6是另一伙，这两个家庭不通！如果按照模板的意思，那么就没有最小生成树！
    这么说是没有问题的，但本题不是求最小生成树，而是求最小生成森林！所以，下面的特判需要注释掉！
    */
    // 4、特判是不是不连通
    // if (cnt < n - 1) res = INF;
}

int main() {
    cin >> n >> m;

    int sum = 0;
    // Kruskal算法直接记录结构体
    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        edge[i] = {a, b, c};
        sum += c;
    }

    kruskal();
    printf("%d\n", sum - res);
    return 0;
}

三、Prim算法

既然题目要求的可能是多个连通块，如果非得用Prim算法的话，是不是得先求出连通块，然后对每个连通块，求出其最小生成树，这样才是最小生成森林呢？

#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;

const int N = 110;

int b[N];

int n, m;
int g[N][N]; // 稠密图，邻接矩阵
int dis[N];  // 这个点到集合的距离
bool st[N];  // 是不是已经使用过
int res;     // 最小生成树里面边的长度之和
int sum;     // 总边长
// 普利姆算法求最小生成树
int prim(int s) {
    // 由于调用多次prim，所以每次需要清零
    memset(dis, 0x3f, sizeof dis);
    dis[s] = 0;
    
    res = 0;
    // 标识
    b[s] = 1;

    for (int i = 0; i < n; i++) { // 迭代n次
        int t = -1;
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || dis[t] > dis[j])) t = j;

        // if (i && dis[t] == INF) return INF; // 非连通图，没有最小生成树
        if (i && dis[t] != INF) res += dis[t], b[t] = 1;
        for (int j = 1; j <= n; j++)
            if (!st[j] && g[t][j] < dis[j]) dis[j] = g[t][j];

        st[t] = true;
    }
    return res;
}

int main() {
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);

    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = c;
        sum += c; // 总边长
    }

    int s = 0;
    for (int i = 1; i <= n; i++)
        if (!b[i]) s += prim(i);

    printf("%d\n", sum - s);
    return 0;
}