8.1 KiB
一、题目描述
给定一张 n 个点的 带权无向图,点从 0∼n−1 标号,求起点 0 到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n。
接下来 n 行每行 n 个整数,其中第 i 行第 j 个整数表示点 i 到 j 的距离(记为 a[i,j])。
对于任意的 x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x], 并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
数据范围
1≤n≤20
0≤a[i,j]≤10^7
输入样例:
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例:
18
二、暴力穷举为什么不行
暴力来做的话,需要确定走的顺序,是一个0到n-1的全排列 ,假设n=5 .就是0号到4号,共5个节点。
0\ 1\ 2\ 3\ 4
0\ 1\ 3\ 2\ 4
0\ 2\ 1\ 3\ 4
0\ 2\ 3\ 1\ 4
0\ 3\ 1\ 2\ 4
0\ 3\ 2\ 1\ 4
共6组,个数是(n-2)!个,(因为首尾是固定的,其它的是全排列)
如果要暴力解决,那么每一组解都需要遍历一次所有节点的权,就是需要一重循环加上去,是n个,就是n * (n-2)!个。n要是20左右的数,就很恐怖了。
三、动态规划为什么行?
动态规划从本质上讲,并没有真正算出所有的可行解是什么,而一般是计算 最大值,最小值,总方案数 等,说白了,就是只计算数量,而不是真的列出来到底是哪些,举个栗子,老师让孩子数一下1到100有多少个数,有的孩子是掰手指头一个个查,最终答案是100,有的孩子聪明,知道1到100是100个数是一个道理。
四、为什么要用状态压缩?
举个栗子:
当有三个布尔类型变量 a、b、c 时,它们的取值只能为 true 或 false。如果要枚举所有可能的取值情况,可以写出如下的代码:
for (bool a = false; a <= true; a++) {
for (bool b = false; b <= true; b++) {
for (bool c = false; c <= true; c++) {
// 枚举所有情况,进行操作
}
}
}
这样的代码嵌套了三层循环,代码看起来十分冗长,而且还不够灵活,如果有更多的变量,循环嵌套的层数将会更多。使用状态压缩,可以将所有变量的取值状态压缩到一个整数中,用循环遍历这个整数即可,代码会变得更加简洁和灵活。
对于上面的例子,可以使用 3 个二进制位来表示变量的取值情况,用 1 表示 true,0 表示 false,共有 2^3=8 种取值情况,分别对应 000、001、010、011、100、101、110、111 这 8 个二进制数。使用一个整数来存储这 3 个变量的取值情况,可以写出如下的代码:
for (int i = 0; i < 8; i++) {
bool a = i & 1;
bool b = i & 2;
bool c = i & 4;
// 对 a、b、c 进行操作
}
在这个例子中,使用了一个整数来存储 a、b、c 三个变量的取值情况,即将三个二进制位拼接成一个整数。通过循环遍历 0 到 7 的整数,将其转化为二进制表示,就可以得到所有的取值情况,然后再将这个整数转化回 a、b、c 三个变量的取值,进行操作。
如果使用二进制描述的话,那么 左移,右移,与,或,非,异或 等操作就是非常自然的,可以很灵活找出两个状态之间的 交集,并集 等,非常方便。
五、状态压缩DP分析
1.本题思路
假设:一共有七个点,用0,1,2,3,4,5,6来表示,那么先假设终点就是5,在这里我们再假设还没有走到5这个点,且走到的终点是4,那么有以下六种情况:
first:0–>1–>2–>3–>4距离:21second:0–>1–>3–>2–>4距离:23third:0–>2–>1–>3–>4距离:17fourth:0–>2–>3–>1–>4距离:20fifth:0–>3–>1–>2–>4距离:15sixth:0–>3–>2–>1–>4距离:18
如果此时你是一个商人你会走怎样的路径?显而易见,会走第五种情况对吧?因为每段路程的终点都是4,且每种方案的可供选择的点是0 \sim 4,而商人寻求的是走到5这个点的最短距离,而4到5的走法只有一种,所以我们选择第五种方案,可寻找到走到5这个点儿之前,且终点是4的方案的最短距离,此时0~5的最短距离为(15+4走到5的距离).(假设4–>5=8)
同理:假设还没有走到5这个点儿,且走到的终点是3,那么有一下六种情况:
first: 0–>1–>2–>4–>3 距离:27
second: 0–>1–>4–>2–>3 距离:22
third: 0–>2–>1–>4–>3 距离:19
fourth: 0–>2–>4–>1–>3 距离:24
fifth: 0–>4–>1–>2–>3 距离:26
sixth: 0–>4–>2–>1–>3 距离:17
此时我们可以果断的做出决定:走第六种方案!!!,而此时0~5的最短距离为(17+3走到5的距离)(假设3–>5=5)
在以上两大类情况之后我们可以得出当走到5时:
1.以4为终点的情况的最短距离是:15+8=23;
2.以3为终点的情况的最短距离是:17+5=22;
经过深思熟虑之后,商人决定走以3为终点的最短距离,此时更新最短距离为:22。
当然以此类推还会有以1为终点和以2为终点的情况,此时我们可以进行以上操作不断更新到5这个点的最短距离,最终可以得到走到5这个点儿的最短距离,然后再返回最初的假设,再依次假设1,2,3,4是终点,最后再不断更新,最终可以得出我们想要的答案。
2、DP分析
用二进制来表示要走的所有情况的路径,这里用i来代替
例如走0,1,2,4这三个点,则表示为:10111; (从右向左读)
走0,2,3这三个点:1101;
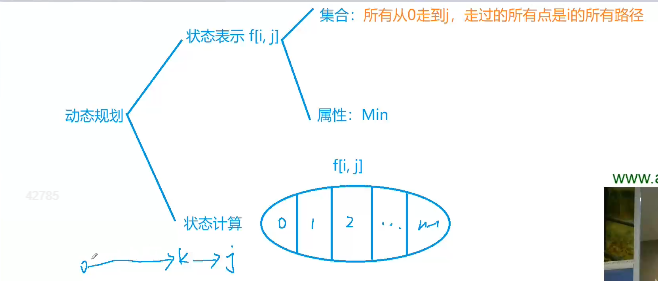
状态表示:
f[i][j]
集合
所有从0走到j,走过的所有点的情况是i的所有路径
属性:
min
状态计算
如1中分析一致,0–>·····–>k–>j中k的所有情况
状态转移方程
\large f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j])六、实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 20; // 好小的上限N,大的没法状态压缩实现,2^N不能太大啊!
const int M = 1 << N; // 2的N次方
int w[N][N]; // 邻接矩阵,记录每两个点之间的距离
int f[M][N]; // DP状态数组,记录每一步的最优解
int n; // n个结点
int main() {
cin >> n;
// 邻接矩阵
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> w[i][j];
// 求最短,设最大
memset(f, 0x3f, sizeof f);
// ① 初始化,从0出发到0结束,路线状态表示为1
f[1][0] = 0; // 从0走到0,路线为1,也就是二进制表示法为(1)_2,表示0出现过
for (int i = 0; i < (1 << n); i++) // 枚举所有路线
for (int j = 0; j < n; j++) // 枚举每个节点作为阶段性终点
if (i >> j & 1) { // 这个节点是不是包含在路径中
for (int k = 0; k < n; k++) // 引入结点k,使得距离更短
// 需要满足i这个路径中除去j这个点,一定要包含k这个点
if ((i - (1 << j)) >> k & 1)
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
}
// 最终经历了所有结点,并且最后停在n-1(最后一个点,因为坐标从0开始)这个点
cout << f[(1 << n) - 1][n - 1] << endl;
return 0;
}