python/TangDou/AcWing/Tree/323.md

AcWing 323 . 战略游戏

一、题目描述

鲍勃喜欢玩电脑游戏，特别是战略游戏，但有时他找不到解决问题的方法，这让他很伤心。

现在他有以下问题。

他必须保护一座中世纪城市，这条城市的道路构成了一棵树。

每个节点上的士兵可以观察到所有和这个点相连的边。

他必须在节点上 放置最少数量的士兵，以便他们可以观察到所有的 边。

你能帮助他吗？

例如，下面的树：

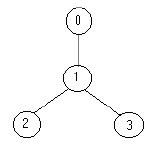
只需要放置 1 名士兵（在节点 1 处），就可观察到所有的边。

输入格式 输入包含多组测试数据，每组测试数据用以描述一棵树。

对于每组测试数据，第一行包含整数 N，表示树的节点数目。

接下来 N 行，每行按如下方法描述一个节点。

节点编号：(子节点数目) 子节点 子节点 …

节点编号从 0 到 N−1，每个节点的子节点数量均不超过 10，每个边在输入数据中只出现一次。

输出格式 对于每组测试数据，输出一个占据一行的结果，表示最少需要的士兵数。

数据范围 0<N≤1500, 一个测试点所有 N 相加之和不超过 300650。

输入样例：

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

输出样例：

1
2

二、算法分析

树形dp，与 AcWing 285 没有上司的舞会 具有对称性

• 没有上司的舞会：每条边上 最多 选择一个点，求最大权值

• 战略游戏：每条边上最少 选择一条点，求最小权值

考虑以结点 u 为 根节点 的子树，该子树所有的 方案，可以由当前结点 放哨兵 或 不放哨兵 进行划分

状态表示

f[u][0]：所有以u为根的子树中选择，并且不选u这个点的方案

f[u][1]：所有以u为根的子树中选择，并且选u这个点的方案

属性 Min

状态计算

当前u结点不选，子结点一定选 f[u][0]=∑(f[v][1])

当前u结点选，子结点可选可不选 f[u][1]=\sum min(f[v][0],f[v][1])

时间复杂度 O(n)

三、Code

#include <bits/stdc++.h>
using namespace std;

const int N = 1510, M = N << 1;
int f[N][2];

// 邻接表
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
/**
 集合：    以结点i为 根节点 的子树，在 i 上放置哨兵(1) 和不放哨兵(0) 的方案
 状态表示： 方案中，放置的哨兵数量 最少
 状态计算：
 */
int in[N]; // 入度

void dfs(int u) {
    for (int i = h[u]; ~i; i = ne[i]) { // 遍历每一条出边
        int v = e[i];
        dfs(v);
        // 状态转移方程
        f[u][0] += f[v][1];               // 节点u不放置哨兵，那么一定要从某一邻接节点放置哨兵
        f[u][1] += min(f[v][0], f[v][1]); // 如果节点u放置了哨兵，那么邻接节点可以选择放置或者不放置
    }
    // u节点选中
    f[u][1] += 1;
}

int main() {
    // n组数据
    int n;

    while (~scanf("%d", &n)) {            // 不断读入数据
        memset(h, -1, sizeof h), idx = 0; // 多组数据，清空邻接表
        memset(in, 0, sizeof in);         // 清空入度数组
        // dp数组也清空一下
        memset(f, 0, sizeof f);
        // n个节点
        for (int i = 1; i <= n; i++) {
            int x, m;
            scanf("%d:(%d)", &x, &m); // scanf可以按格式读入数据
            while (m--) {
                int y;
                scanf("%d ", &y);
                // 添加一条x->y的有向边
                // 数据样例：1出发可以到达2,3;说明是有向图
                add(x, y);
                // 记录y的入度，用于找根节点
                in[y]++;
            }
        }
        // 有向图，找根
        int root = 0;
        while (in[root]) root++;

        // 从根开始
        dfs(root);

        // 输出 两个结果取个 min
        printf("%d\n", min(f[root][0], f[root][1]));
    }
    return 0;
}