python/TangDou/AcWing/TopSort/848.md

##AcWing 848. 有向图的拓扑序列

一、题目描述

给定一个 n 个点 m 条边的有向图，点的编号是 1 到 n，图中可能存在重边和自环。

请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1。

若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。

输入格式 第一行包含两个整数 n 和 m。

接下来 m 行，每行包含两个整数 x 和 y，表示存在一条从点 x 到点 y 的有向边 (x,y)。

输出格式 共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。否则输出 −1。

数据范围 1≤n,m≤10^5

输入样例：

3 3
1 2
2 3
1 3

输出样例：

1 2 3

二、理解与感悟

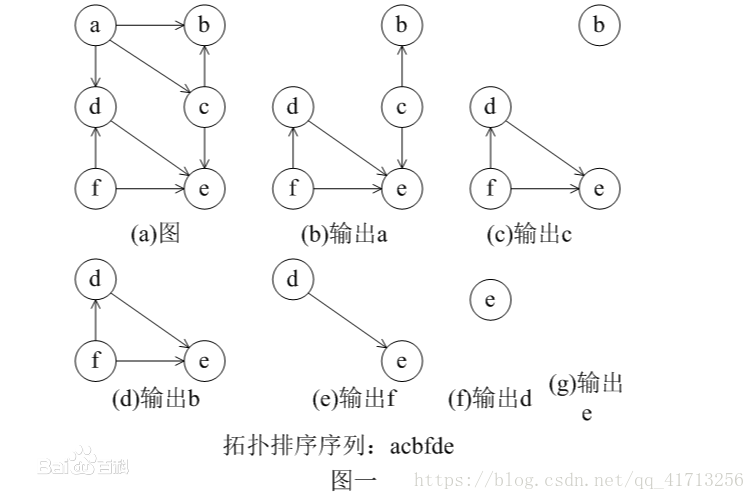
• 拓扑序：在一个有向图中，对所有的节点进行排序，要求没有一个节点指向它前面的节点。

• 有向无环图(DAG)一定有拓扑序列,有向有环图一定没有拓扑序列。

• 出度：从节点出发，有几条边。 出度为零，表示是叶子节点。

• 入度：进入节点，有几条边。 入度为零，表示是根，应该排在拓扑序列最前面的位置。

三、完整代码

#include <bits/stdc++.h>

using namespace std;
const int N = 100010;
int n, m;   // 点数，边数
int ind[N]; // in[N]：入度,所有入度为零的点，可以排在当前最前面的位置。

// 树和图的存储
int h[N], e[N], ne[N], idx;
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
vector<int> path;
// 拓扑
bool topsort() {
    queue<int> q;
    // 扫描所有入度为零的点入队列
    for (int i = 1; i <= n; i++)
        if (!ind[i]) {
            q.push(i);
            path.push_back(i);
        }
    while (q.size()) {
        int u = q.front(); // 队列头
        q.pop();
        for (int i = h[u]; ~i; i = ne[i]) { // 遍历t的所有出边
            int v = e[i];
            if (--ind[v] == 0) { // 入度减1后，是不是为0 (前序依赖为0)
                q.push(v);       // 为0则入队列
                path.push_back(v);
            }
        }
    }
    // 如果一共n个结点进入过队列，则表示存在拓扑序
    return path.size() == n;
}

int main() {
    // 初始化为-1
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int a, b;
        cin >> a >> b;
        add(a, b);
        ind[b]++; // 记录每个结点的入度
    }
    if (!topsort())
        puts("-1");
    else {
        for (int i = 0; i < n; i++) printf("%d ", path[i]);
        puts(""); // 有向无环图的拓扑序不唯一
    }
    return 0;
}