python/TangDou/AcWing/Statemachine/1057.md

##AcWing 1057. 股票买卖 IV

一、题目描述

给定一个长度为 N 的数组，数组中的第 i 个数字表示一个给定股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润，你最多可以完成 k 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。一次买入卖出合为一笔交易。

输入格式 第一行包含整数 N 和 k，表示数组的长度以及你可以完成的最大交易笔数。

第二行包含 N 个不超过 10000 的正整数，表示完整的数组。

输出格式 输出一个整数，表示最大利润。

数据范围 1≤N≤10^5,1≤k≤100

输入样例1：

3 2
2 4 1

输出样例1：

2

输入样例2：

6 2
3 2 6 5 0 3

输出样例2：

7

样例解释 样例1：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

样例2：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。共计利润 4+3 = 7.

二、题目解析

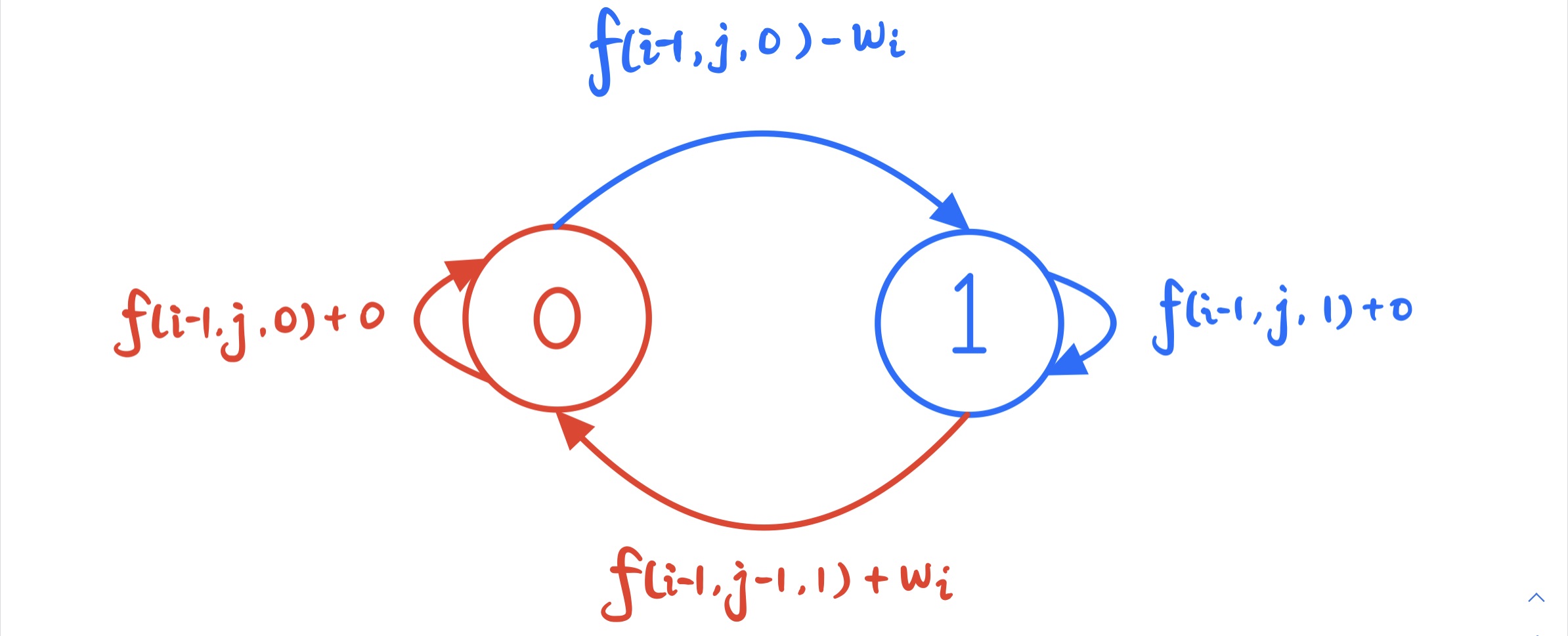
下面以 卖出行为 构成一次完整的交易：

Q:为什么 卖出行为 会构成一次完整的交易,而不是把 买入行为 定义为一次完整的交易呢？要知道，把谁定义为一个完整交易的分界点，是会影响状态转移方程的！ 答:回到递推的起点，我们发现，最初时手中是没有持有股票的，这是一个完整轮回的起点，一个轮回是两个操作：买入，卖出，现在还没有买入，那么经过第一个操作买入后，当然也不是一个轮回结束，只有再执行一个操作卖出后，才又回到手中没有股票的状态，才是一个完整的轮回，这就是为什么以卖出的动作作为一个完整的交易标识的原因。

三、进行到第i天，交易次数恰好是j

这个题目很容易的可以拆分成两种状态: 手中没有股票,手中有股票，用三维数组表示状态：

状态表示

• f[i][j][0] 表示前i天中交易次数 恰好 是j,当前状况为手中没有股票的利益最大值
• f[i][j][1] 表示前i天中交易次数 恰好 是j,当前状况为手中拥有股票的利益最大值

状态转移方程:

f[i][j][0] = max(f[i-1][j][0] , f[i-1][j-1][1] + w[i])

注意：这里是j-1,表示上一次交易是第j-1次，在它执行完卖出后，进入到下一次交易j了

f[i][j][1] = max(f[i-1][j][1] ,f[i-1][j][0] - w[i])

初始化:

结果位置

• 买入不卖一定不是最优解,所以不用枚举f[i][j][1]的状态
• 给定的最大交易数量k,我们不一定都能用了，比如我们用了3次就可以获取到最大利益，没有必要再用1次交易使我们的利益降低不是，所以，每个f[n][i][0]都有可能是最大价值，需要遍历一次找出最大值。

Code

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10, M = 110;

int n, k;
int w[N];
int f[N][M][2];
// 以卖出做为一次完整交易的分界线
// 二维定义是恰好
int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; ++i) cin >> w[i];

    memset(f, -0x3f, sizeof f);                  // 其它状态目前是无效状态或者是未知状态
    for (int i = 0; i <= n; i++) f[i][0][0] = 0; // 0次交易，手中无股票，最大收益是0

    for (int i = 1; i <= n; i++) {     // 枚举每一天
        for (int j = 0; j <= k; j++) { // 枚举到这一天时，恰好进行了j次交易

            // ① 这个 if(j) 可以理解为先把后面的状态转移方程写出来，再观察一下，发现j>=1，否则数组索引出负值
            // ② 现实意义理解：如果 j=0时，就是上面进行的初始值是固定值，不需要转移
            // ③ 手中无股票的状态，可以由前一天手中无股票的状态，和，前一天手中有股票但卖出了，两种状态转移而来
            // ④ 最开始时，手中无股票，定义是原点，现在又到了手中无股票的状态，这是一个轮回，所以卖出是一个完整交易的临界点
            if (j) f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j - 1][1] + w[i]);

            // ⑤ 手中有股票，要么是昨天手中股票，继续持有，要么是昨天手中无股票，购入了
            f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j][0] - w[i]);
        }
    }

    int res = 0;
    for (int i = 0; i <= k; i++) res = max(res, f[n][i][0]);

    cout << res << endl;
    return 0;
}

四、进行到第i天，交易次数最多是j

状态表示

• f[i][j][0] 表示前i天中交易次数 最多 是j,当前状况为手中没有股票的利益最大值
• f[i][j][1] 表示前i天中交易次数 最多 是j,当前状况为手中有股票的利益最大值

状态转移方程: f[i][j][0] = max(f[i-1][j][0] , f[i-1][j-1][1] + w[i]) f[i][j][1] = max(f[i-1][j][1] ,f[i-1][j][0] - w[i])

与恰好的状态转移方程是一样的，差别在于初值不同

初始化:

结果位置

• f[n][k][0]

Code

#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 1e5 + 10, M = 110;

int n, k;
int w[N];
int f[N][M][2];
// 以卖出做为一次完整交易的分界线
// f[i][j][0/1]定义成 前i天 完成最多是j次交易 且 决策为0/1的集合
int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> w[i];

    memset(f, -0x3f, sizeof f);

    for (int i = 0; i <= n; i++) f[i][0][0] = 0;
    for (int j = 0; j <= n; j++) f[0][j][0] = 0;

    // 下面两句，由于整体进行了初始化，就变得可以省略了
    // for (int i = 0; i <= n; i++) f[i][0][1] = -INF;
    // for (int j = 0; j <= n; j++) f[0][j][1] = -INF;

    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= k; j++) {
            if (j) f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j - 1][1] + w[i]);
            f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j][0] - w[i]);
        }
    }
    cout << f[n][k][0] << endl;
    return 0;
}