python

5.3 KiB

Raw Permalink Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

##AcWing 853. 有边数限制的最短路

一、题目描述

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，边权可能为负数。

请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离，如果无法从 1 号点走到 n 号点，输出 impossible。

注意：图中可能存在负权回路。

输入格式 第一行包含三个整数 n,m,k。

接下来行，每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

点的编号为 1∼n。

输出格式 输出一个整数，表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。

如果不存在满足条件的路径，则输出 impossible。

数据范围 1≤n,k≤500,1≤m≤10000,1≤x,y≤n，任意边长的绝对值不超过 10000。

输入样例：

输出样例：

输出样例：

图解算法见这里

陈小玉老师的视频

二、`Bellman-Ford`算法

Bellman-Ford算法的实现方式是每一次都对图中的所有边进行一次松弛操作，对于边(u,v):dist[v] = min(dist[v],dist[u] + w)，每一轮都对边进行操作，当某一轮没有边再发生松弛操作即可停止。

在最短路存在的前提下，那么我们每一次的松弛操作都应当让最短路的边数+1，而最短路最多只有n-1条边，故最多循环n-1次，即可得出结果，而每次对边进行松弛时间复杂度是O(m)，故总时间复杂度是O(nm)。

Bellman-Ford算法还可以检测图中是否存在负权环，当循环松弛操作n-1次后，第n次操作仍然有边发生了松弛操作，那么就意味着n个点的最短路可以拥有n条边，因此必然存在环，但一般判断负环不使用Bellman-Ford算法，而是用优化后的版本SPFA算法，包括求最短路也是，那么Bellman-Ford算法还有什么优势呢？优势就在于本题，有边数限制的最短路问题只能用Bellman-Ford算法来求解。

需要注意的点：

① 每次松弛的时候，是使用上次松弛完的结果来计算本次的结果，因此计算的时候需要备份一次上次的结果，以免发生“串联更新”的问题，也就是使用本次松弛计算的结果来更新后续的结果；

② 输出答案时，可能存在负权边更新了两个无法到达的点的情况，所以判断不能直接判断是否等于0x3f，比如1无法到达点5，也无法到达点7，但5->7的边权是-2，那么在每次松弛的时候，是会导致这个值变小一点点的。

要点总结

bellman-ford可以处理负权边,而Dijkstra只能处理正权边。
bellman-ford算法可以处理负权回路，因为它求得的最短路是有限制的，是限制了边数的，这样不会永久的走下去，会得到一个解；
SPFA算法各方面优于该算法，但是在碰到 限制了最短路径长度 时就只能用bellman-ford了，此时直接把n重循环改成k次循环即可

三、实现代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
const int INF = 0x3f3f3f3f;
int n, m, T;
// 邻接表
int idx, e[N], ne[N], h[N], w[N];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int backup[N]; // 拷贝一下d数组,避免出现串联
int d[N];      // 最短距离

int bellman_ford() {
    memset(d, 0x3f, sizeof d);
    d[1] = 0;

    while (T--) {
        memcpy(backup, d, sizeof d);            // 每次更新前memcpy避免出现串联
        for (int u = 1; u <= n; u++)            // 执行n次松驰操作
            for (int i = h[u]; ~i; i = ne[i]) { // 枚举每个出边
                int v = e[i];
                d[v] = min(d[v], backup[u] + w[i]);
            }
    }
    if (d[n] > INF / 2) return INF; // 因为有负权边所以可能出现d[n]比0x3f3f3f3f稍微小一些
    return d[n];
}
int main() {
    cin >> n >> m >> T;
    memset(h, -1, sizeof h);
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    int t = bellman_ford();
    if (t == INF)
        puts("impossible");
    else
        cout << t << endl;
    return 0;
}

四、答疑时间

Q:为什么使用了>INF/2这样的代码？

比如说这样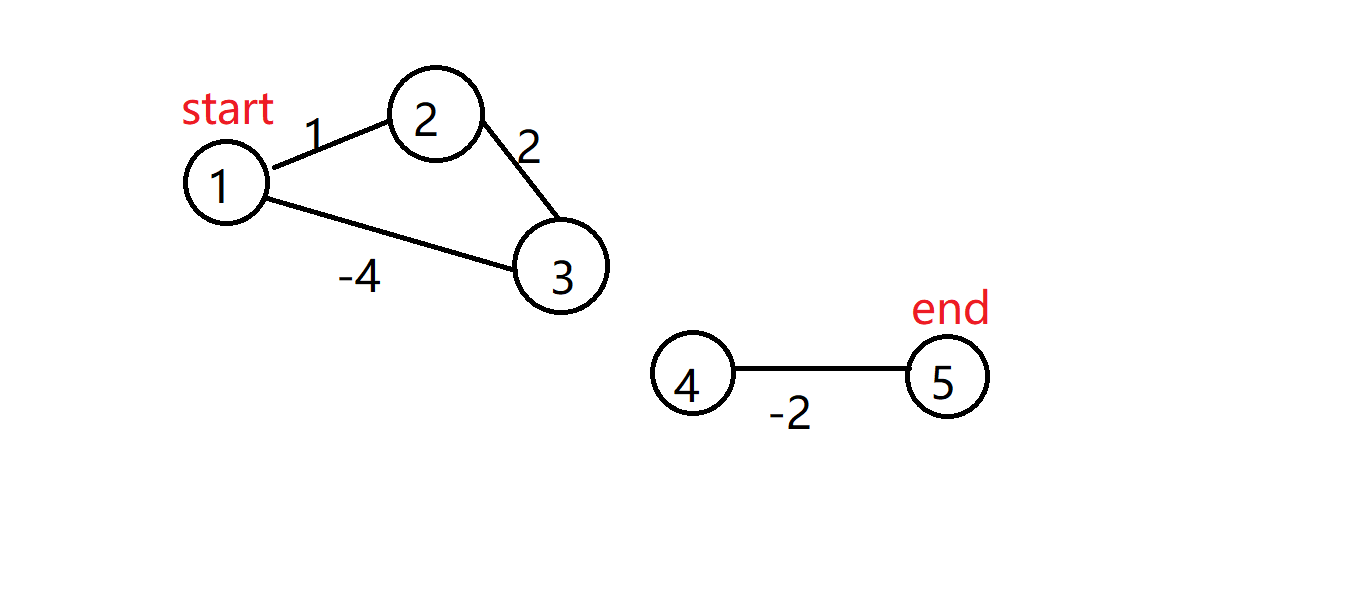：这个奇葩起点和终点居然不连通 4号点在经过松弛操作后可能会更新5号点，因为正无穷-2<正无穷嘛所以终点就不是正无穷了，所以就返回正无穷-2了，不对又因为如果正无穷减也不会减的太大（数据保证边权的绝对值不大于100000）

所以就直接这样写

if(d[n]>=0x3f3f3f3f/2)return INF;
return d[n];

5.3 KiB Raw Permalink Blame History Unescape Escape