python/TangDou/AcWing/SegmentTree/ZKW/ZKW线段树.md

zkw 线段树

参考博文I 这篇英文文献还是要看一下的，有意思~ 参考博文II

俗称 重口味 ，与 KMP 类似，咳咳... 只要没标记，我都写 zkw 线段树。。 只要有标记，我都写递归版线段树。。

一、ZKW线段树简介

ZKW线段树是由清华大学姚班大佬 张昆玮 所创立的一种线段树储存结构，由于其基于非递归的实现方式以及精简的代码和较高的效率而闻名。甚至，ZKW线段树能够可持久化。

我们从算法的角度对基础线段树进行分析：其实线段树算法本身的本质仍是统计。因此我们可以从统计的角度入手对线段树进行分析：线段树是将一个个数轴划分为区间进行处理的，因此我们面对的往往是一系列的离散量，这导致了我们在使用时的线段树单纯的退化为一棵"点树"(即最底层的线段树只包含一个点)。基于这一点可以入手对线段树进行优化。

二、ZKW线段树的构造原理

首先，我们忽略线段树中的数据，从线段树的框架结构入手进行分析：如图所示是一颗采用堆式储存的基本线段树：

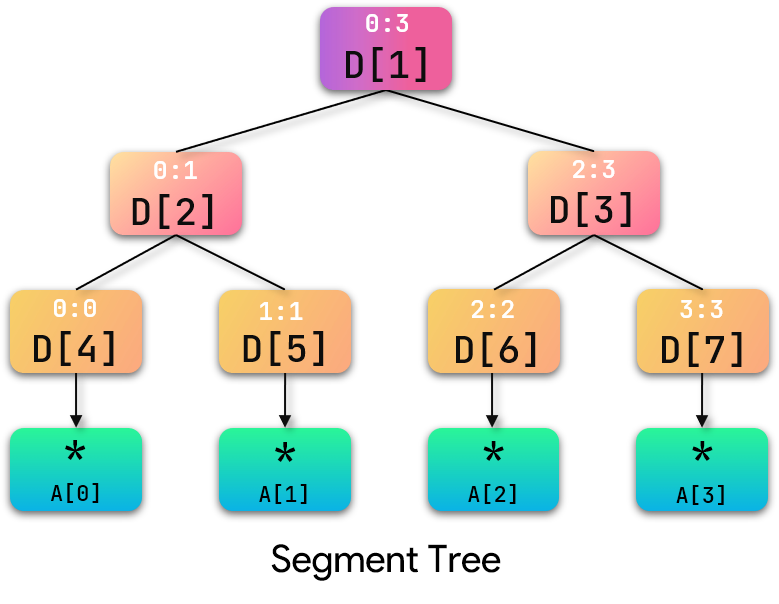
我们将节点编号转换为二进制：

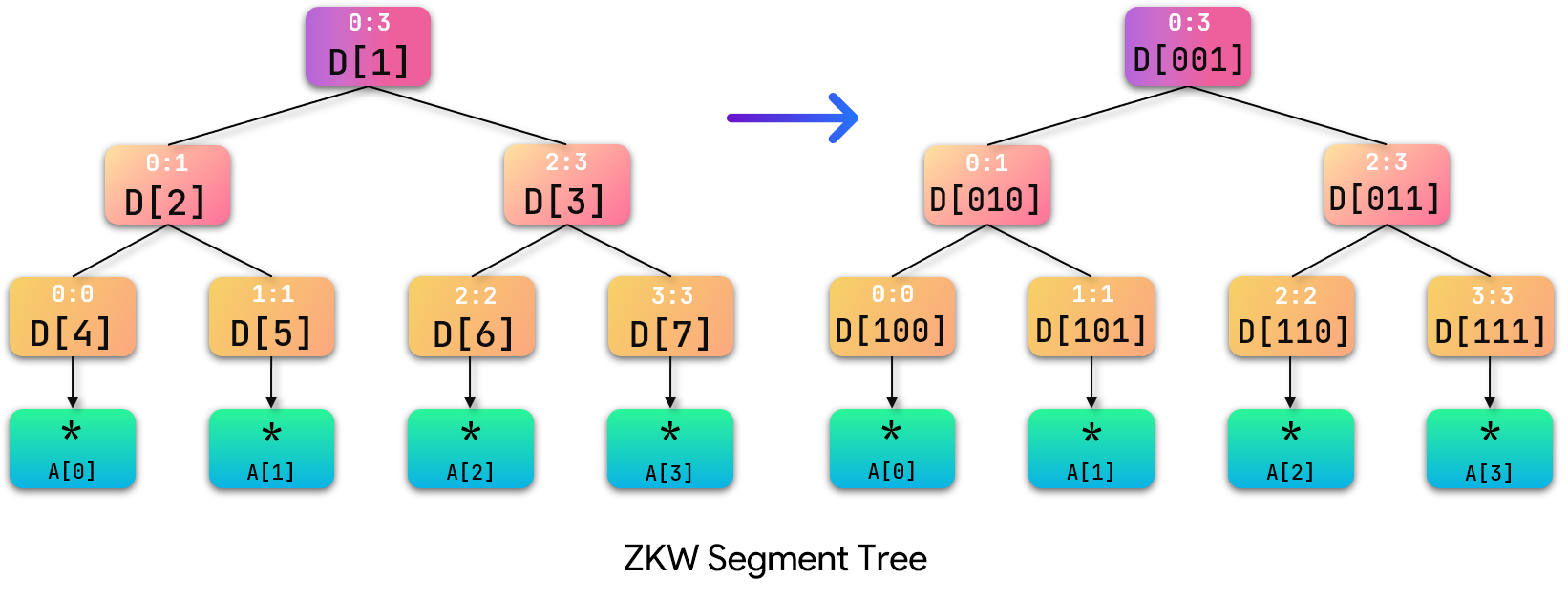
观察转为二进制后的结点规律：在基础线段树的学习中，我们知道对于任意结点x，其左子节点为x<<1，右子节点为x<<1 ∣ 1。这个规律是我们从根结点出发向叶节点寻找的规律。那么现在我们换个思路：从叶结点出发向根结点寻找规律：

• 当前结点的父节点一定是当前的结点右移一位(舍弃低位)得到的
• 当前结点的左子节点为x<<1，右子节点为x<<1 ∣ 1
• 每一层结点按照顺序排列，第n层有2^{n-1}个节点
• 最后一层的结点个数 = 值域

因为最后一层的结点个数=值域，假设给定数组a[n]，含有元素a[1] \sim a[n]。

我们约定，无论元素的个数是否达到2^n，最后一层的空间都开到2^n，无数据的叶节点空置即可。

三、ZKW线段树基本操作

1.建树操作

void build(int n){
    for(m = 1; m <= n;) m <<= 1;
    for (int i = m + 1; i <= m + n; ++i) op_array[i] = read();
    for (int i = m - 1; i; --i) operation(),
}

• 如果维护区间和，那么op\_array[] \rightarrow sum[]，operation

sum[i] = sum[i << 1] + sum[i << 1 | 1];

• 如果维护区间最小值，那么op\_array[] \rightarrow minn[]，operation

minn[i] = min(minn[i << 1], minn[i << 1 | 1])；	//不支持修改操作

minn[i] = min(minn[i << 1], minn[i << 1 | 1]),
minn[i << 1] -= minn[i], minn[i << 1 | 1] -= minn[i];

• 如果维护区间最大值，那么op\_array[] \rightarrow maxx[]，operation

maxx[i] = max(maxx[i << 1], maxx[i << 1 | 1]);	//不支持修改操作

maxx[i] = max(maxx[i << 1], maxx[i << 1 | 1]),
maxx[i << 1] -= maxx[i], maxx[i << 1 | 1] -= maxx[i];

2.单点查询

这个操作是相对容易理解的，就是一个从叶子结点开始，不断向父节点走，同时累加沿路的权值的过程。

int query(int x){
    int ans = 0;
    for (x += m; x; x >>= 1) ans += minn[s];
    return ans;
}

3.单点修改

单点修改的思路非常简单，只需要修改当前结点并更新父节点即可。

void update(int x,int v){
    op_array[x = m + x] += v;
    while(x) operation();
}

• 如果维护区间和，那么op\_array[] \rightarrow sum[]，operation:

sum[i] = a[i << 1] + a[i << 1 | 1];

//如果单纯维护区间和，那么可以压行：
void update(int p, int k){ for (p += m; p; p >>= 1) sum[p] += k; }

• 如果维护区间最小值，那么op\_array[] \rightarrow minn[]，operation

minn[i] = min(minn[i << 1], minn[i << 1 | 1]),
minn[i << 1] -= minn[i], minn[i << 1 | 1] -= minn[i];

• 如果维护区间最大值，那么op\_array[] \rightarrow maxx[]，operation

maxx[i] = max(maxx[i << 1], maxx[i << 1 | 1]),
maxx[i << 1] -= maxx[i], maxx[i << 1 | 1] -= maxx[i];

4.区间查询

如何进行区间查询？我们继续二进制表示入手，寻找查询的规律。

在实际的查询中，我们采取扩增左右区间端点的方式进行查询，即：将闭区间转换为开区间查询。

我们以下图为例：假设要查询的区间为[1,2]，那么首先转换为开区间(0,3)，我们可以发现变为开区间之后，0的兄弟结点必在区间之内，3的兄弟结点​必在区间内；根据这个规律我们可以总结：

对于待查区间[l,r]：

• 如果l是左儿子，则其兄弟结点必位于区间之内；
• 如果r是右儿子，则其兄弟结点必位于区间之内；
• 查询的终止条件：两个结点同为兄弟；
• 以上结论，对于任意层的结点均成立。

我们通过例子来模拟这个过程：

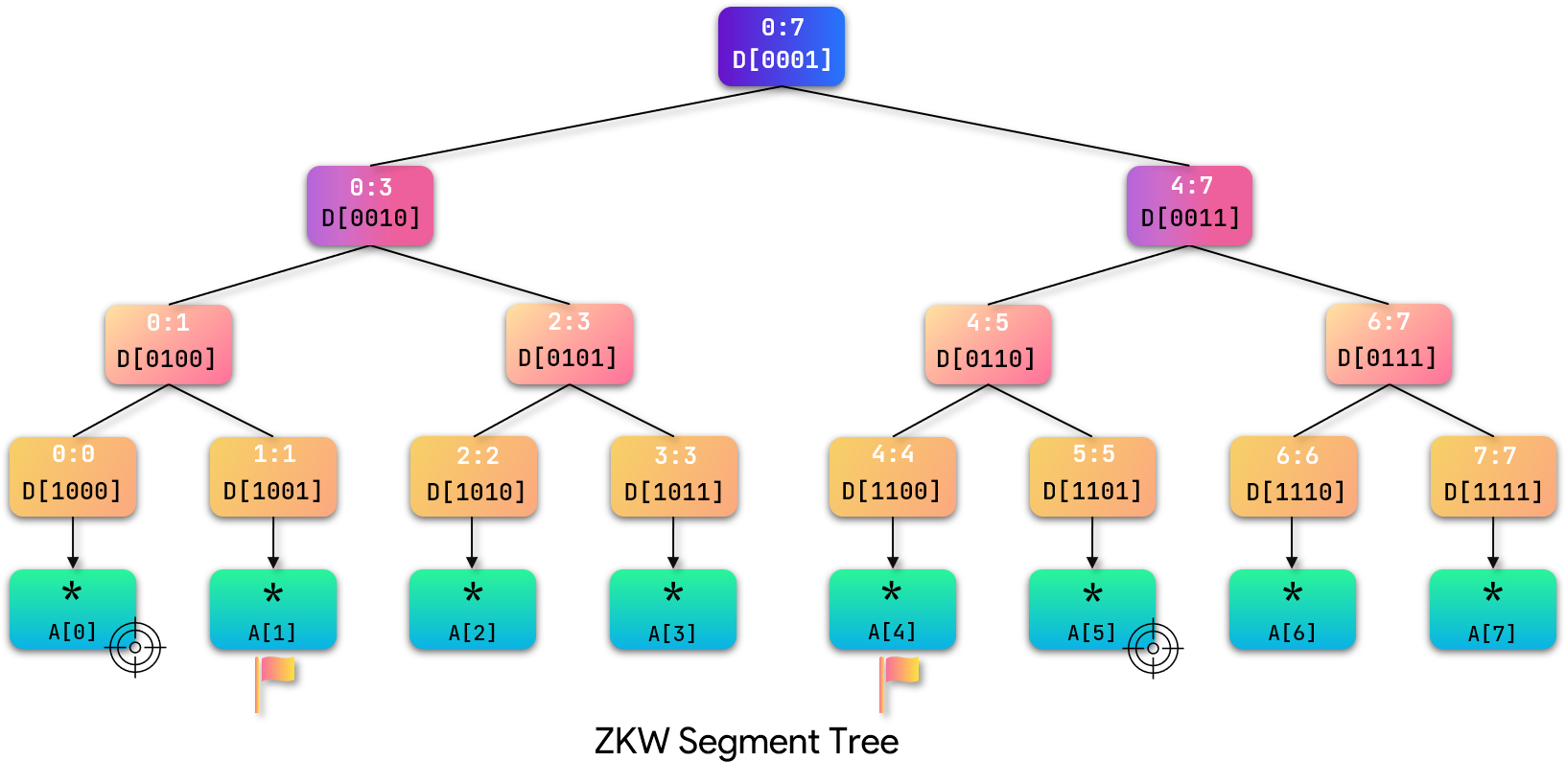
在如图所示的ZKW线段树中，假设我们要查询区间[1,4]，那么步骤如下：

• 闭区间改开区间，[1,4]改为查询(0,5)，扩增至(M + 0, M + 5) = (8, 13)；

• 判断：左端点D[1000_B]是左儿子，那么其兄弟D[1001_B]必位于区间内，累加ans + = D[1001_B] 判断：右端点D[1101_B]是右儿子，那么其兄弟D[1100_B]必位于区间内，累加ans + = D[ 1100_B]

• 缩小区间(向根结点缩)：l > > = 1 → 1000 >> 1 = 0100 ， r > > = 1 → 1101 > > 1 = 0110

• 判断：左端点D[0100_B]是左儿子，那么其兄弟D[0101_B]必位于区间内，累加an s + = D[0101_B] 判断：右端点D[0110_B]是左儿子，不做操作；

• 缩小区间(向根结点缩)：l >> = 1 → 0100 > > 1 = 0010 ， r > > = 1 → 0110 > > 1 = 0011

• 此时l和r同为兄弟，因此终止查询。

我们可以总结出区间查询的步骤：

• 闭区间改开区间[l, r] → ( l + M − 1 , r + M + 1 )
• 判断当前区间左端点是否是左儿子，如果是，则向累加器中累加兄弟结点； 判断当前区间右端点是否为右儿子，如果是，则向累加器中累加兄弟结点；
• 端点变量处理操作：l > > = 1 , r > > = 1
• 循环执行2 − 3的步骤，直到l和r同为兄弟结点(此时不终止会导致重复计算)

如何判断是否为左子节点？我们很容易观察到左右子节点共同的特征：左子节点最低位为0 ，右子节点最低位为1，那么我们可以通过以下操作的真值判断左右子节点

• 判断左子节点：∼l & 1 l % 2 == 0的意思
• 判断右子节点：r & 1
r % 2 == 1的意思

对于取兄弟结点的值则可以通过与1异或求得：

• 左子节点求兄弟结点：l xor 1
• 右子节点求兄弟结点：r xor 1

延绵的山峰 无修改维护最值

/*
延绵的山峰
★★☆ 输入文件：climb.in 输出文件：climb.out 简单对比
时间限制：1 s 内存限制：512 MB
问题描述
有一座延绵不断、跌宕起伏的山，最低处海拔为0，最高处海拔不超过8848米，从这座山的一端走到另一端的过程中，
每走1米海拔就升高或降低1米。有Q个登山队计划在这座山的不同区段登山，当他们攀到各自区段的最高峰时，就会插上队旗。
请你写一个程序找出他们插旗的高度。

输入文件
第1行，一个整数N(N<=10^6)，表示山两端的跨度。
接下来N+1行，每行一个非负整数Hi，表示该位置的海拔高度，其中H0=Hn=0。

然后是一个正整数Q(Q<=7000)，表示登山队的数量。
接下来Q行，每行两个数Ai, Bi，表示第i个登山队攀爬的区段[Ai,Bi]，其中0<=Ai<=Bi<=N。

输出文件
Q行，每行为一个整数，表示第i个登山队插旗的高度。

样例输入
10
0
1
2
3
2
3
4
3
2
1
0
5
0 10
2 4
3 7
7 9
8 8

样例输出
4
3
4
3
2
*/
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100010;
// 快读
int read() {
    int x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return x * f;
}

int d[N << 2], m;

//构建zkw线段树
void build(int n) {
    for (m = 1; m < n;) m <<= 1;                                  // 强行开够（大于n）方便二进制访问叶节点
    for (int i = 1; i <= n; i++) d[m + i] = read();               //对zkw的叶子节点赋值
    for (int i = m; i; i--) d[i] = max(d[i << 1], d[i << 1 | 1]); //待所有叶子节点有值后，统一执行一次向上数据统计信息汇总
}

//区间查询最大值
int query(int l, int r) {
    int ans = 0;
    for (l = l + m - 1, r = r + m + 1; l ^ r ^ 1; l >>= 1, r >>= 1) {
        if (~l & 1) ans = max(d[l ^ 1], ans);
        if (r & 1) ans = max(d[r ^ 1], ans);
    }
    return ans;
}

int main() {
//文件输入输出
#ifndef ONLINE_JUDGE
    freopen("Cogs58.in", "r", stdin);
#endif
    int n, q, l, r;
    /*
    第1行，一个整数N(N<=10^6)，表示山两端的跨度。
    接下来N+1行，每行一个非负整数Hi，表示该位置的海拔高度，其中H0=Hn=0。
    */
    n = read(), n++; // H0~Hn 共n+1行，而且，题目告诉我们H0=Hn=0,会在输入数据时给出,所以，一共是n+1点

    //构建
    build(n);

    q = read();
    for (int i = 1; i <= q; i++) {
        l = read(), r = read();
        printf("%d\n", query(l + 1, r + 1));
    }
    return 0;
}

I Hate It HDU - 1754 单点更新，区间查询

#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;

const int N = 2e5 + 1000;
// 快读
int read() {
    int x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return x * f;
}
// zkw线段树
int d[N << 2];

int n; // n个叶子节点
int q; // q个操作,区间查询或单点修改
int m; // m是指所有父节点们的个数

void pushup(int x) {
    for (int i = (m + x) >> 1; i; i >>= 1) d[i] = max(d[i << 1], d[i << 1 | 1]);
}

//单点修改并psuhup
void modify(int x, int c) {
    d[m + x] = c;
    pushup(x);
}

//构建重口味树
void built() {
    memset(d, 0, sizeof d);
    for (m = 1; m <= n + 1;) m <<= 1; // 强行开够（大于n）方便二进制访问叶节点
    for (int i = 1; i <= n; i++) d[m + i] = read();               //初始值
    for (int i = m; i; i--) d[i] = max(d[i << 1], d[i << 1 | 1]); //待所有叶子节点有值后，统一执行一次向上数据统计信息汇总
}

//区间查询
int query(int l, int r) {
    int ans = -1;
    // 闭区间改为开区间：l=l+m-1 : 将查询区间改为l-1, r=r+m+1 : 将查询区间改为r+1
    // l^r^1 : 相当于判断l与r是否是兄弟节点
    for (l = l + m - 1, r = r + m + 1; l ^ r ^ 1; l >>= 1, r >>= 1) {
        if (~l & 1) ans = max(ans, d[l ^ 1]); // l % 2 == 0 左端点 是左儿子 max(右子树)，想像一下题解中0号端点（哨兵），肯定是%2=0
        if (r & 1) ans = max(ans, d[r ^ 1]);  // r % 2 == 1 右端点 是右儿子 max(左子树)，想像一下题解中1号端点，肯定是%2=1
    }
    return ans;
}

//方法重载，单点查询 [本题没有用到，用来做模板的]
int query(int x) {
    return d[m + x]; //直接返回结果的zkw线段树节点值
}

int main() {
//文件输入输出
#ifndef ONLINE_JUDGE
    freopen("HDU1754.in", "r", stdin);
#endif
    char op[2];
    while (~scanf("%d%d", &n, &q)) {
        //构建zkw树
        built();

        while (q--) {
            scanf("%s", op);
            int l = read(), r = read();
            if (op[0] == 'Q')
                printf("%d\n", query(l, r));
            else
                modify(l, r);
        }
    }
    return 0;
}

HDU 1166 敌兵布阵 单点增加，区间查询

#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

//快读
int read() {
    int x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return x * f;
}

const int N = 50000 + 10;

int m = 1, n;
int d[N << 2];

//区间查询
int query(int l, int r) {
    int ans = 0;
    for (l = l + m - 1, r = r + m + 1; l ^ r ^ 1; l >>= 1, r >>= 1) {
        if (~l & 1) ans += d[l ^ 1];
        if (r & 1) ans += d[r ^ 1];
    }
    return ans;
}

//向上更新统计信息
void pushup(int x) {
    for (int i = (m + x) >> 1; i; i >>= 1) d[i] = d[i << 1] + d[i << 1 | 1];
}

//单点增加
void add(int x, int c) {
    d[m + x] += c;
    pushup(x);
}

void build(int n) {
    memset(d, 0, sizeof d);
    for (m = 1; m < n;) m <<= 1; // 强行开够（大于n）方便二进制访问叶节点
    for (int i = 1; i <= n; i++) d[m + i] = read();           //初始值
    for (int i = m; i; i--) d[i] = d[i << 1] + d[i << 1 | 1]; //待所有叶子节点有值后，统一执行一次向上数据统计信息汇总
}

int main() {
//文件输入输出
#ifndef ONLINE_JUDGE
    freopen("HDU1166.in", "r", stdin);
#endif
    int k = read();

    for (int q = 1; q <= k; q++) {
        n = read();
        //构建zkw线段树
        build(n);

        printf("Case %d:\n", q);

        char op[10];
        while (scanf("%s", op)) {
            if (op[0] == 'E') break;
            int l = read(), r = read();
            if (op[0] == 'Q')
                printf("%d\n", query(l, r));
            else if (op[0] == 'A')
                add(l, r);
            else if (op[0] == 'S')
                add(l, -r);
        }
    }
    return 0;
}

5.区间修改

参考题解

在普通的线段树中，一般用 lazy tag 来解决这个问题，zkw线段树同样可以，但从上向下操作、下放 lazy tag 等操作并不优雅,常数大。

可以采用 标记永久化，随用随查，按zkw的说法——永久化的标记就是值。

考虑上文提到的区间操作的过程，自下向上走的过程中，根据遇到的标记来计算贡献。

对于一个节点，若修改操作对节点所代表的整个区间产生影响，显然我们可以直接对该节点进行标记，而非逐层递归修改。 那么，在自底向上的线段树中，我们可以不下传标记，而是在每一次查询时，统计累加一路上所有标记对答案产生的影响，这种标记思想被称为标记永久化。

区间修改 关于标记永久化，我们进行定义：add[i]代表线段树中i号节点的关键值已经进行修改，但是其所有子节点均有一个值为add[i]的增量未进行处理。

设置两个开区间指针l,r，并同时向上遍历。同时，我们维护三个变量lc,rc,c，分别代表:

• 当前左端点走到的子树有多少个元素在修改区间内
• 当前右端点走到的子树有多少个元素在修改区间内
• 当前层叶子节点个数

利用上述变量和add标记的定义，沿路更新add标记和原线段树即可，当然，对于l,r成为兄弟后，我们还须将add标记一直上推到根节点。

区间求和 有了add标记，我们就很容易求得区间的和了: 将闭区间转换为开区间，然后向上遍历，

同样维护lc,rc,c，然后利用add标记进行累加，再加上原来的区间和，就能得到答案。

例题P3372 【模板】线段树 1

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
#define LL long long
#define N 100010

//对于区间修改 区间求和的zkw线段树，最重要的思想就是标记永久化的思想

//快读
LL read() {
    LL x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return x * f;
}
int n, q, m;
LL sum[N << 2], add[N << 2];

void build() {
    for (m = 1; m <= n;) m <<= 1;
    for (int i = 1; i <= n; i++) sum[m + i] = read();
    for (int i = m - 1; i >= 1; i--) sum[i] = sum[i << 1] + sum[i << 1 | 1];
}

void modify(int l, int r, int d) {
    int lc = 0, rc = 0, c = 1;
    // 开区间，从左右叶子端点出发，如果l和r不是兄弟节点，就一路向上
    // lc 表示当前左端点走到的子树有多少个元素在修改区间内
    // rc 表示当前右端点走到的子树有多少个元素在修改区间内
    // c 当前层叶子节点个数
    for (l = m + l - 1, r = m + r + 1; l ^ r ^ 1; l >>= 1, r >>= 1, c <<= 1) {
        sum[l] += d * lc, sum[r] += d * rc;                        //自底向上，更新统计信息sum和
        if (~l & 1) add[l ^ 1] += d, sum[l ^ 1] += d * c, lc += c; // l % 2 == 0 左端点 是左儿子 右子树完整在区间内
        if (r & 1) add[r ^ 1] += d, sum[r ^ 1] += d * c, rc += c;  // r % 2 == 1 右端点 是右儿子 左子树完整在区间内
    }
    //是兄弟节点时，需要一路向上到根进行推送
    for (; l || r; l >>= 1, r >>= 1) sum[l] += d * lc, sum[r] += d * rc;
}

//区间查询
LL query(int l, int r) {
    LL lc = 0, rc = 0, c = 1;
    LL res = 0;
    for (l = m + l - 1, r = m + r + 1; l ^ r ^ 1; l >>= 1, r >>= 1, c <<= 1) {
        if (add[l]) res += add[l] * lc;
        if (add[r]) res += add[r] * rc;
        if (~l & 1) res += sum[l ^ 1], lc += c;
        if (r & 1) res += sum[r ^ 1], rc += c;
    }
    for (; l || r; l >>= 1, r >>= 1) res += add[l] * lc, res += add[r] * rc;
    return res;
}

int main() {
//文件输入输出
#ifndef ONLINE_JUDGE
    freopen("P3372.in", "r", stdin);
#endif
    n = read(), q = read();

    build();
    for (int i = 1; i <= q; i++) {
        int op = read();
        int l = read(), r = read();
        if (op == 1) {
            int c = read();
            modify(l, r, c);
        } else
            printf("%lld\n", query(l, r));
    }
    return 0;
}

五、总结

简单总结一下，上面也说过，这东西除了卡常就没什么用，还不见得有原版线段树好写

实战中一般不会有人特意放 zkw 过然后卡递归线段树

感觉实用性甚至不如什么猫树

不过思想还可以，值得学学

运行情况对比: P3372 【模板】线段树 1

版本1：zkw线段树+标记永久化 第10个测试点 44ms/3.75MB 版本2：zkw线段树+pushup+pushdown 第10个测试点 85ms/5.87MB 版本3：zkw线段树+cf_zkw变异版本，内存2*N 第10个测试点 60ms/2.71MB 版本4：树状数组+差分 第10个测试点 31ms/2.36MB 版本5：递归版本普通线段树 第10个测试点 105ms/8.33MB

总结： (1) 普通线段树最牛B，没有之一，对，你没有看错，因为大家基本上是一个级别的， 比最快的仅仅慢3倍而已，我过不了，你估计也过不了，因为出题人一般都是卡一个复杂度的，卡常数不容易。 ZKW这个东东，没有必要再花时间研究了，因为快也快不到哪里去，还徒增学习的时间，不划算。

(2) 有哪些问题是线段树可以解决但树状数组解决不了的？ 树状数组可以维护前缀和（或后缀和），维护不了一般的区间和，而线段树可以轻松维护。 这里的“和”是指一种满足结合律的运算的累算，例如普通加/乘法、最大/小值、矩阵乘法、 最大公约数等等。可以求差的运算也可以用树状数组维护前缀和来计算区间和， 比如普通加法的区间和是两个前缀和的差， 可以很容易支持 区间修改+单点询问 或 单点修改+区间询问，但没法很好地同时支持 区间修改+区间询问（有时也可以强行懒惰更新）。

不能求差的运算，树状数组就维护不了区间和了，比如区间最大/小值、区间最大公约数。 其实树状数组只是线段树的一个特殊形式，因为不需要询问前缀以外的子区间，需要维护的信息更少， 把线段树上的一些不需要的节点删去了。