17 KiB
一、题目描述
给出一个可重集 a(编号为 1),它支持以下操作:
0 p x y:将可重集 p 中大于等于 x 且小于等于 y 的值移动到一个新的可重集中(新可重集编号为从 2 开始的正整数,是上一次产生的新可重集的编号+1)。
1 p t:将可重集 t 中的数放入可重集 p,且清空可重集 t(数据保证在此后的操作中不会出现可重集 t)。
2 p x q:在 p 这个可重集中加入 x 个数字 q。
3 p x y:查询可重集 p 中大于等于 x 且小于等于 y 的值的个数。
4 p k:查询在 p 这个可重集中第 k 小的数,不存在时输出 -1。
输入格式
第一行两个整数 n,m,表示可重集中的数在 1\sim n 的范围内,有 m 个操作。
接下来一行 n 个整数,表示 1 \sim n 这些数在 a 中出现的次数 (a_{i} \leq m)。
接下来的 m 行每行若干个整数,第一个数为操作的编号 opt(0 \leq opt≤4),以题目描述为准。
输出格式 依次输出每个查询操作的答案。
二、线段树的分裂 & 合并
网上找线段树合并/分裂的博客,讲得很清楚的也不多,某些部分只有自己 yy 一下了。
前置芝士: ① 权值线段树,② 动态开点线段树
在以下讨论中,我们设 值域 都为 [1,n] 中的整数。
先定义代码中的一些东西:
ch[i][0] 表示 i 的左子结点,ch[i][1] 表示 i 的右子结点,val[i] 表示 i 点维护的值(出现了多少个该值域中的数)
一、线段树合并
有时我们需要 整合两棵权值线段树的信息 ,这个整合的过程称为 线段树合并。我们以最简单的合并为例:将两棵树相加。
两棵树如何相加呢?在权值线段树上,每个点维护了一个当前区间中数的个数,而数的个数是可以相加的,这个合并的过程可以理解为:把两个可重集合并,对应的权值线段树上发生的过程。而相加的原理很简单,两棵同构的线段树,只需要对应位置相加即可,如图:
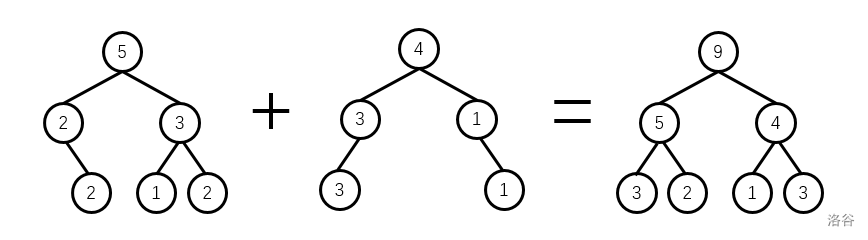
注意动态开点线段树上某些点是缺的,其值当然是 0。
如何合并两棵线段树呢?
暴力是很简单的,我们枚举 1 到 n,将第二棵树中对应位置上的值在第一棵树上做单点修改即可。
这个方法可以用 启发式合并 进一步优化,但只能适用于一些特殊情况(比如说如果带了分裂或者一个值在多棵树上出现,启发式合并就歇菜了)。
而我们可以递归处理线段树合并,设我们现在要合并的是以 x,y 为根的两棵子树,要确保它们在线段树上处于同一位置(即它们是两棵树上代表同一区间的点)。
如果 x,y 其中一个为 0 (也就是某个权值线段树上没有这个位置的点),无需合并,返回另一个非 0 的点即可。
否则,我们先合并 x,y 的左右子结点,再根据两子结点的信息整合得到 x,y 合并的结果。
线段树合并一般有两种写法:新建结点和不新建结点。但是两者原理是一样的。
新建结点的写法:
新建一个结点 p 作为 x,y 合并的结果。将 ch[x][0] 和 ch[y][0] 的合并结果记为 sl,ch[x][1] 和 ch[y][1] 的合并结果记为 sr,令 sl,sr 分别为 p 的两个子结点,对 p 做一次 pushup 即可得到结果。此后 x,y 就没有用的,可以回收(节省空间的方法)。但是有时 x,y 的信息不能丢,这时就不能回收。
(这里原先的代码有点问题,先删了)
不新建结点的写法:
如果一个点合并完就可以扔掉,那还可以写得更加简便,直接将 x 作为合并后的结果,将 y 的值加到 x 上即可(直接对应位置相加),甚至不需要 pushup,但是注意,如果 x=0,返回的是 y,所以比较保险的写法是 x=merge(x,y)。
事实上这里我们连当前区间的左右端点 l,r 也可以去掉,因为到叶结点后 ch[x][i] 自然是 0,自然会返回。
int merge (int x,int y) {
if (!x||!y) {return x+y;} // 只有一边有点,不用合并
val[x]+=val[y]; // 信息整合
ch[x][0]=merge(ch[x][0],ch[y][0]);
ch[x][1]=merge(ch[x][1],ch[y][1]);
del(y); // 垃圾回收
return x;
}
这东西看着很一般,复杂度怎么样呢?
单独讨论一次合并的复杂度没有什么意义,如果两棵树都是满的,复杂度就到 O(n) 了,所以一般从均摊角度来讨论。
如果现在有 m 棵线段树(每棵树初始只有一个位置有权值),经过若干次合并最后变成 1 棵,此过程的复杂度是多少呢?
例题:
P4556 [Vani有约会]雨天的尾巴 /【模板】线段树合并
不说具体怎么做了,这些题都有很完整的题解,我就分析一下复杂度(这些题都符合上面提到的模型)。
一开始有 m 棵树,只有一个位置有权值,所以一棵树上结点数量为 O(logn),m 棵树的结点总数也就是 O(mlogn)。
分析上面的代码,发现每一次进入 merge 函数,要么停止递归,要么继续递归并有一个点被垃圾回收。显然停止递归的 merge 次数与继续递归的 merge 次数同阶(不继续递归的情况是从递归的情况出来的,不会超过其两倍的数量)。
因此整个过程的复杂度就等于继续递归的 merge 函数进入次数的复杂度(每一次执行 merge 在不考虑递归时复杂度 O(1)),也就等同于被删除的结点个数,是不超过 O(mlogn) 的(有点像势能分析?)。
注意复杂度本身和是否回收结点没有关系,只是借以分析而已。
所以整个过程的复杂度也就是 O(mlogn)。
但是线段树合并的复杂度不总是对的,不过本题中 1 操作的复杂度我不知道是否是均摊 logn 的,希望有人能证明/证伪一下。
二、线段树分裂
将一个可重集前 k 小的数与之后的数分成两个集合,那么对应的权值线段树就要裂成两棵权值线段树。
举个栗子:将 [1,3] 和 [4,4] 分开(这里为了方便直接用权值描述了,一般是按照第 k 小的位置来的):
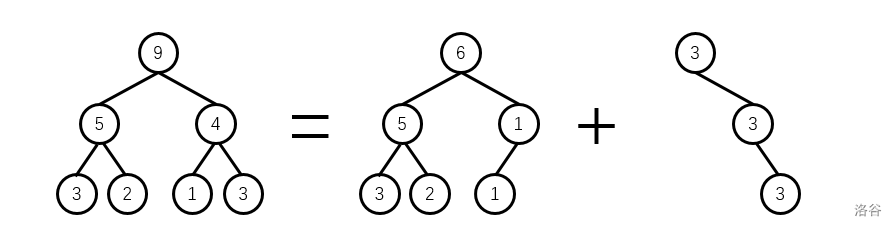
暴力当然也很简单,找到第 k,后面的值新建一棵树,在原树上减掉即可。
然而我们可以仿照 FHQ Treap 的套路,实现 O(logn) 的分裂。
设我们现在要将以 x 为根的树分裂成 x,y 为根的这两棵树(y 本来是不存在的,传引用),以第 k 小为界,前 k 小在 x,之后的在 y。
首先看 x 的左子树的值 v,如果 v<k,那么左侧依然归 x(不需要处理),递归右侧即可,注意 k 变成了 k-v。
如果 v=k,那么左边归 x,右边归 y 即可。
如果 v>k,那么右边归 y,递归左侧即可。
看完结构后看权值,x 的新权值当然是 k,那么 y 的权值也就是 x 原先的权值减去 k 了。
可以发现,如果 v\ge k,那么 y 的右子结点都是需要赋值的,下面的代码直接归到了同一句里(else 所在的那一句):
void split (int x,int &y,ll k) {
y=newnod();
ll v=val[ch[x][0]];
if (k>v) {split(ch[x][1],ch[y][1],k-v);}
else {swap(ch[x][1],ch[y][1]);} // 右子树归 y,x 的右子树变成 0
if (k<v) {split(ch[x][0],ch[y][0],k);}
val[y]=val[x]-k;
val[x]=k;
return;
}
这个每次只递归一边,复杂度是 O(\log n) 没啥问题。
三、这道题
每个操作分别来看。
将 [x,y] 分裂出来:先分出 [1,x-1],再从 [x,n] 中分出 [x,y] 和 [y+1,n],最后把 [1,x-1] 和 [y+1,n] 合并。我注意到 std 不是这样的,std 的分裂写的就是分裂出一个区间,我在这里用了一次合并,但是复杂度是对的,稍后会证明复杂度为 O(\log n);
将 t 树合并入 p 树:单次合并即可,不确定复杂度,但是不超过 2\times 10^3次总没问题的;
p 树中插入 a 个 q:单点修改,复杂度 O(\log n);
查询 [x,y] 中数的个数:区间求和,复杂度 O(\log n);
查询第 k 小:经典操作,复杂度 O(\log n)。
最后说一下 0 操作的复杂度:
两次分裂是 O(\log n) 没问题,主要看合并。注意合并的两个区间没有交集,我们就看一看每一层会涉及几个点。
对于第 1 层:总共就 1 个点...
对于第 i 层:如果第 i-1 层只递归下来 1 个点(设为 u),再设 x 和 y 为 u 的左右子结点。如果前一棵树占了 x,y 两个点,那么因为后一棵树占的区间严格在前一棵树之后,所以只会占 y,那么需要递归的只有 y,反过来的话同理需要递归的只有 x,所以第 i 层也只需要递归 1 个点。
每一层只往下递归一个点,复杂度就是 O(\log n) 了。
三、实现代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
//重定向输入输出
#define FILE_OUT freopen("P5494.out", "w", stdout);
#define FILE_IN freopen("P5494.in", "r", stdin);
//重定义 tr[u].l 和 tr[u].r 快速录入用
#define ls tr[u].lson
#define rs tr[u].rson
const int N = 200010;
int n, m;
int a[N]; //记录原始数组,其实也可以不用保存,直接在build时录入到叶子也可以
int root[N], idx; //分裂出的第几个线段树,idx是序号维护器
struct Node {
int lson, rson; //动态开点,记录左右儿子的节点编号
//注意:这里与普通线段树不同,没有记录当前节点的管辖范围!!!!!
//黄海尝试了记录[l,r]的方法,结果因为结构体内增加了两个属性,同时数组的上限非常大,直接MLE了好多测试点。
LL val; //每一个节点保存的值大小是管辖区间中的个数
} tr[N << 6];
int cnt; //记录tr数组中的可以放入节点的位置
//权值线段树合并,维护区间元素个数
void pushup(int u) {
tr[u].val = tr[ls].val + tr[rs].val;
}
/**
* @brief 构建线段树
*
* @param l 想要创建的节点,是管理哪个范围的,这与普通线段树相似,只不过普通线段树可以事先准备好节点号,这个需要现用现创建,
* 并且需要返回节点号,让父节点记录和父节点的关联关系。
* @param r
* @return int
*/
int build(int l, int r) {
//由于构建之前,空间是未分配状态,需要为新构建的节点分配节点号,节点号就是cnt
int u = ++cnt;
//现在有了可用的节点号了
if (l == r) { //如果是叶子节点
//接下来一行n个整数,表示 1∼n 这些数在a[N]中出现的 **次数**
//其实7就放在[7,7]的位置上,val就记录7这个数字出现的次数
tr[u].val = a[l]; //个数!!!
return u;
}
int mid = (l + r) >> 1;
//由于是动态开点,无法像普通线段树一样,采用预先创建的办法,普通办法只要知道父节点,u<<1 和 u<<1|1就是左右儿子节点号
//而在动态开点的模板中,需要递归创建并返回新建节点编号,由并记录到tr[u].l和tr[u].r上,以实现父子节点的关联对应
ls = build(l, mid), rs = build(mid + 1, r);
//更新父节点统计信息
pushup(u);
return u;
}
/**
* @brief 线段树分裂
*
* @param k 以k为根的线段树
* @param l 左边界
* @param r 右边界
* @param ql 要分裂出的左边界
* @param qr 要分裂出的右边界
* @return int
*/
int spilt(int k, int l, int r, int ql, int qr) {
int u = ++cnt; //分裂后的根节点编号u
if (l == ql && r == qr) { //完全命中区间
tr[u] = tr[k]; //将tr[k]抄到tr[u]
tr[k].val = tr[k].lson = tr[k].rson = 0; //销毁tr[k]
return u; //返回新分裂后的节点编号u
}
int mid = (l + r) >> 1;
if (qr <= mid) //分裂左儿子
ls = spilt(tr[k].lson, l, mid, ql, qr);
else if (ql > mid) //分裂右儿子
rs = spilt(tr[k].rson, mid + 1, r, ql, qr);
else {
ls = spilt(tr[k].lson, l, mid, ql, mid);
rs = spilt(tr[k].rson, mid + 1, r, mid + 1, qr);
}
//递归更新分裂后u和k的父节点信息
pushup(u), pushup(k);
return u;
}
//合并线段树
void merge(int &x, int y) {
if (!(x && y))
x |= y;
else {
tr[x].val += tr[y].val;
merge(tr[x].lson, tr[y].lson);
merge(tr[x].rson, tr[y].rson);
}
}
/**
* @brief 在 u 这个可重集中加入 x 个数字 q
*
* @param u 以u为根
* @param l 左边界
* @param r 右边界
* @param q 数字p
* @param x 增加x个
*/
void insert(int u, int l, int r, int q, int x) {
if (l == r) {
tr[u].val += x; //权值线段树个数增加x个
return;
}
int mid = (l + r) >> 1;
if (q <= mid) {
if (ls == 0) ls = ++cnt; //左儿子不存在,则创建之
insert(ls, l, mid, q, x); //向左儿子递归插入
} else {
if (rs == 0) rs = ++cnt; //右儿子不存在,则创建之
insert(rs, mid + 1, r, q, x); //向右儿子递归插入
}
//向父节点更新统计信息
pushup(u);
}
/**
* @brief 在以u节点为根的线段树中,管辖范围是[l,r],查询区间[ql,qr]内数字的总个数
* 查询可重集 p中大于等于 x 且小于等于 y 的值的个数。
* @param u 根节点
* @param l 左边界
* @param r 右边界
* @param ql 查询左边界
* @param qr 查询右边界
* @return LL 有多少个
*/
LL query(int u, int l, int r, int ql, int qr) {
if (l == ql && r == qr) return tr[u].val;
int mid = (l + r) >> 1;
if (qr <= mid)
return query(ls, l, mid, ql, qr);
else if (ql > mid)
return query(rs, mid + 1, r, ql, qr);
else
return query(ls, l, mid, ql, mid) + query(rs, mid + 1, r, mid + 1, qr);
}
//查询第k小的数
int kth(int u, int l, int r, int k) {
if (l == r) return l;
int mid = (l + r) >> 1;
if (tr[ls].val >= k)
return kth(ls, l, mid, k);
return kth(rs, mid + 1, r, k - tr[ls].val);
}
int main() {
// OJ的环境不使用文件输入输出
#ifndef ONLINE_JUDGE
FILE_IN
FILE_OUT
#endif
//优化读入
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
//范围[1~n],创建第一个线段树,返回值是根节点号,记录到root[1]中
for (int i = 1; i <= n; i++) cin >> a[i];
root[++idx] = build(1, n);
int op, p, x, y;
for (int i = 1; i <= m; i++) {
cin >> op >> p;
if (op == 0) { //将可重集p中大于等于x且小于等于y的值放入一个新的可重集中
//新可重集编号为从2开始的正整数,是上一次产生的新可重集的编号+1。
cin >> x >> y;
root[++idx] = spilt(root[p], 1, n, x, y);
} else if (op == 1) { //合并线段树
cin >> x;
merge(root[p], root[x]); //将根为x的线段树合并到根为p的线段树中去,x线段树以后就不用了
} else if (op == 2) { //在p这个可重集中加入x个数字q
cin >> x >> y;
insert(root[p], 1, n, y, x);
} else if (op == 3) { //区间查询
cin >> x >> y;
printf("%lld\n", query(root[p], 1, n, x, y));
} else {
int k;
cin >> k; //在线段树上二分,如果左孩子的元素个数大于等于k,说明第k小在左子树内;
//否则,在右子树内。
if (query(root[p], 1, n, 1, n) < k)
printf("-1\n");
else
printf("%d\n", kth(root[p], 1, n, k));
}
}
return 0;
}