python/TangDou/AcWing/SegmentTree/P5490.md

###P5490 【模板】扫描线

一、题目描述

求 n 个四边平行于坐标轴的矩形的面积并。

输入格式

第一行一个正整数 n。

接下来 n 行每行四个非负整数 x_1, y_1, x_2, y_2，表示一个矩形的四个端点坐标为 (x_1, y_1),(x_1, y_2),(x_2, y_2),(x_2, y_1)。

输出格式

一行一个正整数，表示 n 个矩形的并集覆盖的总面积。

样例输入

2
100 100 200 200
150 150 250 255

输出样例

18000

提示

对于 20\% 的数据，1 \le n \le 1000。
对于 100\% 的数据，1 \le n \le {10}^5，0 \le x_1 < x_2 \le {10}^9，0 \le y_1 < y_2 \le {10}^9。

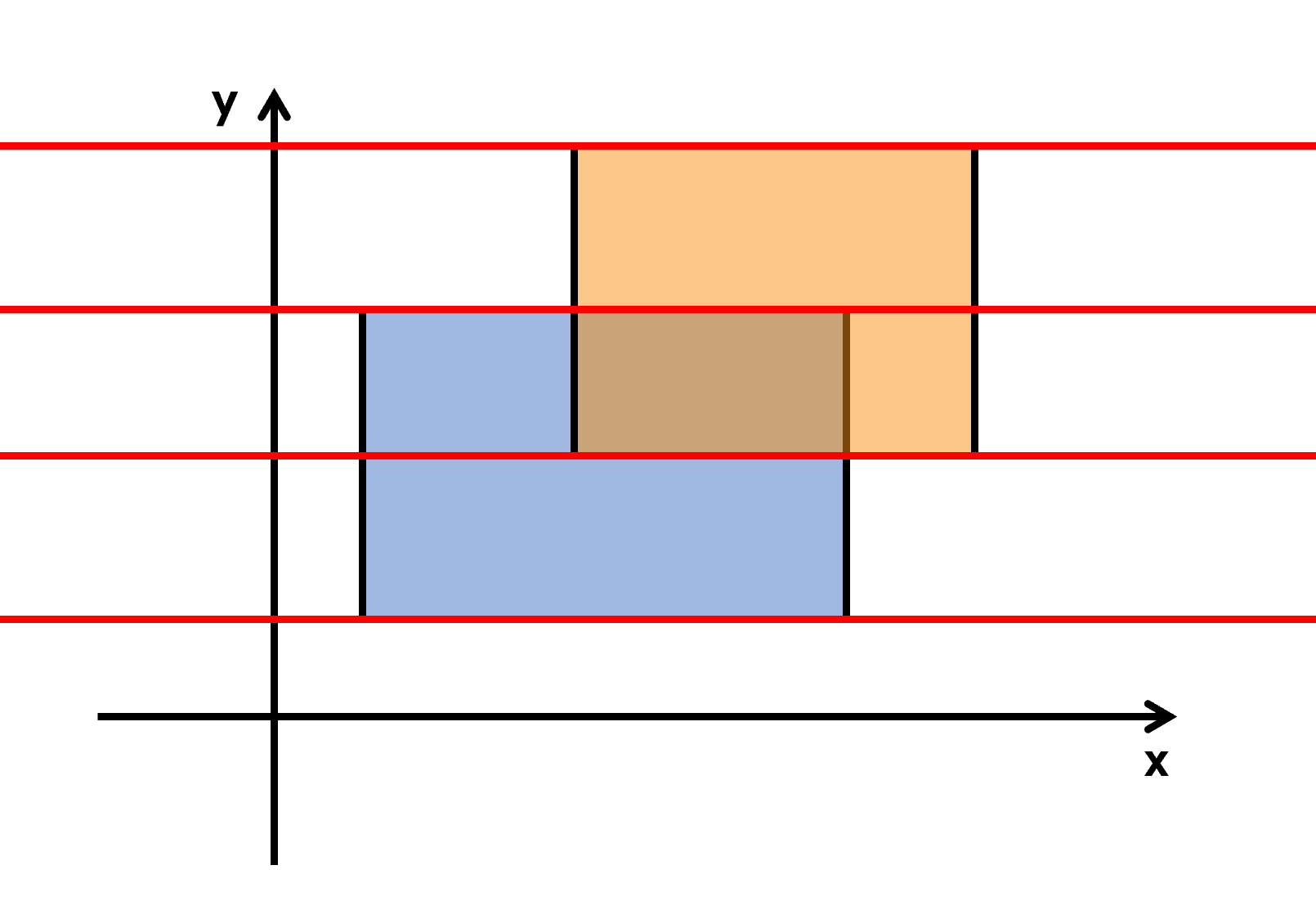
由于都是矩形，因此运用扫描线以后，面积的求法其实可以简化为 \sum截线段长度×扫过的高度。这也是扫描线算法最基础的应用。

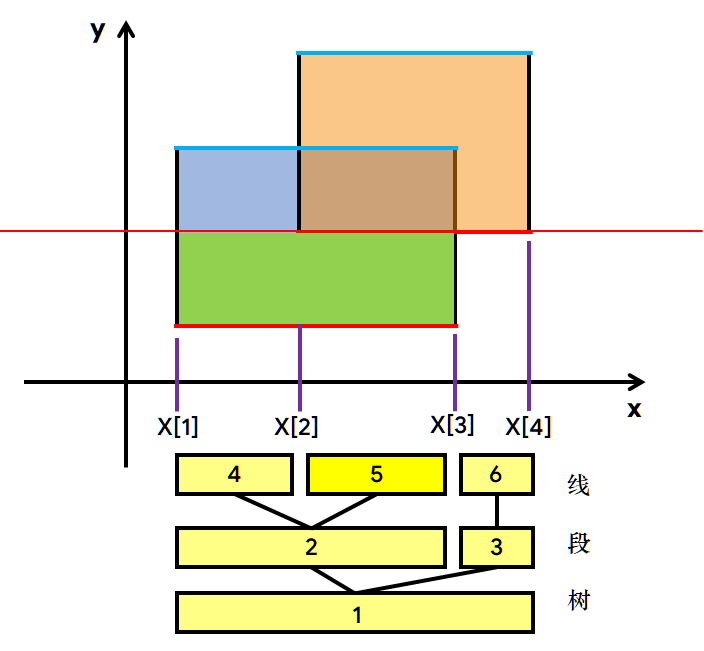
考虑以下这个简单的例子。

问题在于如何才能模拟扫描线从下向上扫过图形，并且快速计算出当前扫描线被截得的长度。

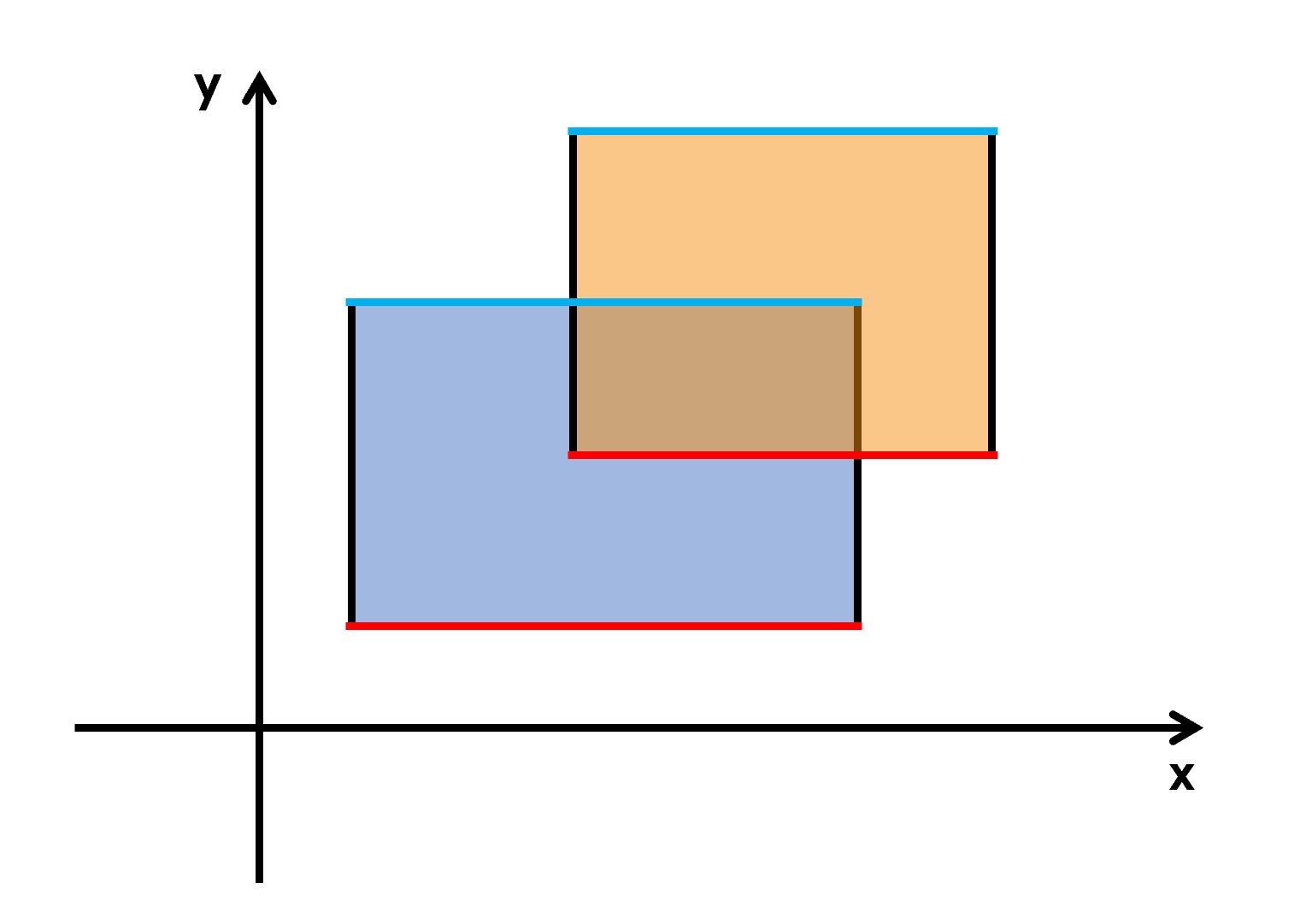
现在假设，扫描线每次会在碰到横边的时候停下来，如图。

简单来说，可对图形面积产生影响的元素，也就是这些横边左右端点的坐标。

为了快速计算出截线段长度，可以 将横边赋上不同的权值，具体为：对于一个矩形，其下边权值为1，上边权值为−1。

然后把所有的横边按照y坐标升序排序。这样，对于每个矩形，扫描线总是会先碰到下边，然后再碰到上边。那么就能保证扫描线所截的长度永远非负了。

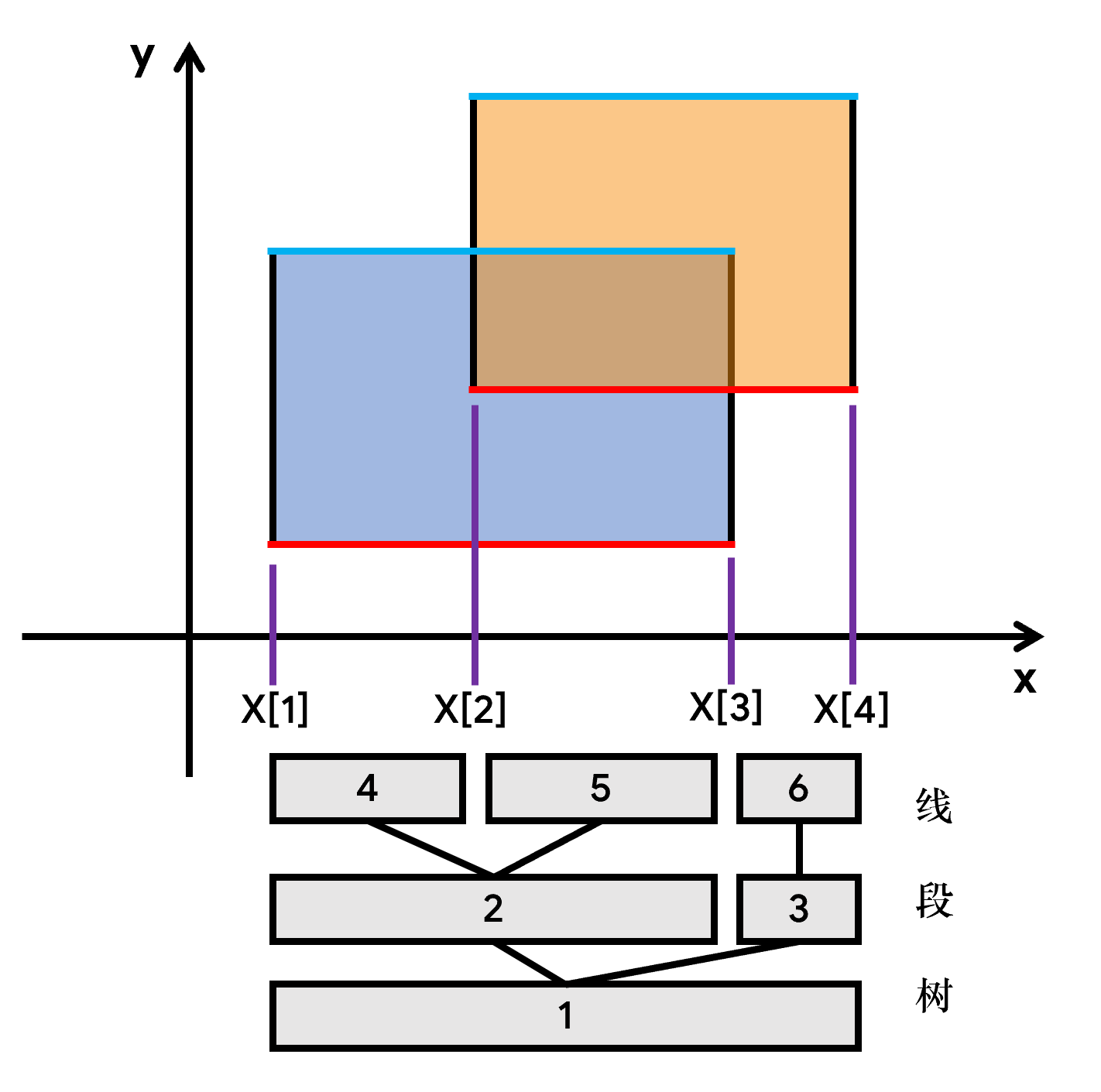
这样操作以后，就可以和线段树扯上关系。先把所有端点在x轴上离散化（其实就是把所有点的横坐标存到X[]里，然后升序排个序，最后去重）。

在这个例子中，4个端点的纵投影总共把x轴切割成了5部分。取中间的3部分线段，建立一棵线段树，其每个端点维护 一条线段（也就是一个区间）的信息：

1. 该线段被覆盖了多少次（被多少个矩形所覆盖）。
2. 该线段内被整个图形所截的长度是多少。(有效长度)

显然，只要一条线段被覆盖，那么它肯定被图形所截。所以，整个问题就转化为了一个 区间查询问题，即：每次将 当前扫描线扫到的边 对应的信息 按照之前赋上的权值更新，然后再查询线段树根节点的信息，最后得到当前扫描线扫过的面积。这就可以用线段树来实现了（毕竟人家叫 线段 树嘛）。

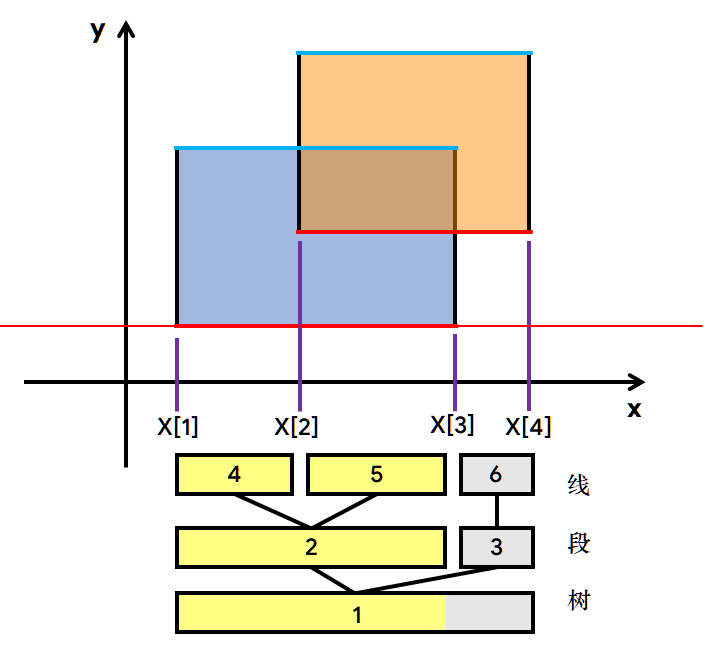
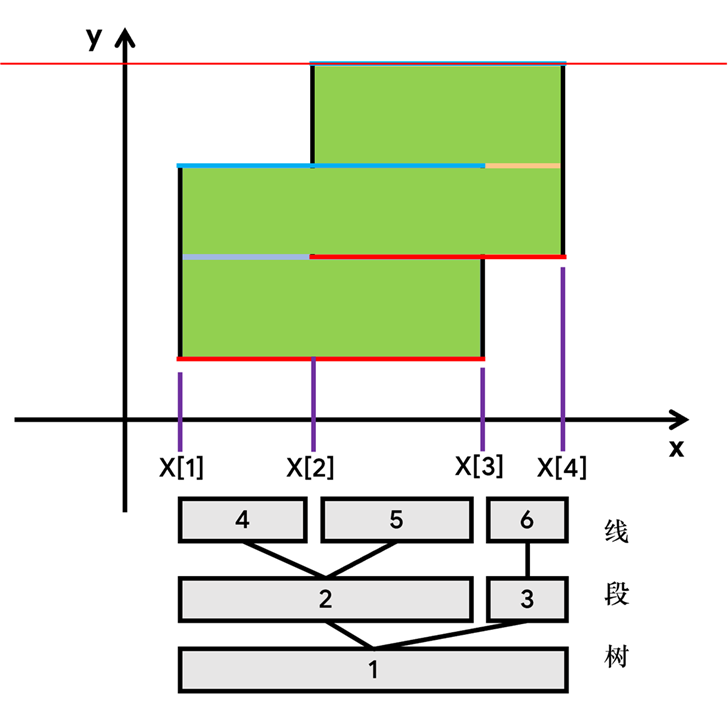
下面是模拟的过程：

注：上图的5号节点的sum=2，绿色部分表示已计算的面积。

还剩下一个棘手的问题： Q1:线段树到底该怎么建？保存什么信息？怎么在节点间传递信息？

这里我使用自己最习惯的线段树写法，个人感觉这样的逻辑最清晰。

先看下面的建树过程：

void build(int u, int l, int r) {
    tr[u]={l,r};//这个可以清空其它统计信息，属性信息等
    //tr[u].l = l, tr[u].r = r;//这个就不能清空了，如果是多组测试数据，记得要memset(tr,0,sizeof tr); 否则就会WA，我不告诉你我是怎么知道的~
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
}

我们已经知道，这棵 线段树的每个节点都对应了一条线段。考虑 将线段树上节点对应的区间和横边 建立 映射关系。先看对于一个叶子节点x，建树时保证了tr[u].l=tr[u].r，但其保存的信息很显然不可能只是某条线段的一个端点（如果一条线段的两个端点重合，那么它实质上仅是一个点）。再看一个节点的左右儿子，同样地，建树的时候已经保证了左右儿子的区间不会重合（交集为空），但是看这样两条相邻线段：[1,2],[2,3],你会发现 [1,2]∩[2,3]=\{2\}，也就是说左儿子的右端点和右儿子的左端点其实是重合的。所以如果想得太简单，就gg了。

注：GG，竞技游戏礼貌用语，Good Game的缩写，来源于韩国星际比赛，指在竞技游戏（如魔兽争霸、星际争霸、反恐精英、DOTA、LOL等 ）中，纯粹就是习惯性的向对手表示欣赏，类似于比武结束后的行礼，意思是“打得好，我认输”。后来也常用于现实生活中表示“失败”的场景。也就是我输了，完蛋了的意思~

考虑把线段树每个节点x对应的区间（tr[u].l,tr[u].r）不变，改变区间和横边的映射关系， 具体为：节点x对应[X[tr[u].l],X[tr[u].r+1]]这条横边。可以看到，这里很机智地把右端点的对应关系给改了下，于是就兼容了。

注意： 变量名 y_1 在<cmath>库里头有定义，会冲突，所以不开bits库就好。

Q2:线段树里保存的是什么？用来干什么？

答：线段树只是一个基础的数据结构，它的作用是可以以比较快的时间获取到区间的某些统计和。 在扫描线中，通过预先的按x由小到大排序，然后从左向右进行扫描，遇到一条竖线时，获取到它的x坐标 和y_1,y_2 两个坐标

通过line[i + 1].x - line[i].x就可以提前知道本竖线与下一条竖线间的距离是多少，也就是一个小矩形的宽，而高是y_2-y_1。

但是，我们遇到的不一定就是一条竖线时，只有一段，可能是多段，那么，这个有效的len就可能是多条竖线的有效长度叠加和。

如何快速计算这个有效长度的叠加和呢？答案就是用线段树。

总结：线段线中保存的是y轴的竖的小线段！

y轴上的数据范围可是很大的，最大1e9,直接原封不动的将y轴坐标映射到线段树中，肯定GG,需要进行离散化。

那么只进行了离散化就行了吗？离散化不是万能的，它只能解决将范围大、稀疏的数据映射到范围小、连续的一段内，其它的问题它可以管理不了。

还有什么其它的问题呢？

比如在坐标系中有两个线段 [1,2],[2,3]，如果映射到线段树中去呢？一对一映射吗？那肯定不行，因为我们发现两个集合有交集，而线段树是不能有交集的。那怎么办呢？

办法就是左闭右开，即[1,2),[2,3),也就是在线段树中是[1,1],[2,2]这两个叶子节点！换句话说，在坐标系中的右端看来需要减1才能映射到线段树中

设坐标系中扫描线区间段的范围为[L,R],那么映射到线段树中的节点(当然是指离散化后)就是(l,r)->[L,R-1] 即 l=L,r=R-1

已知r求R,就是R=r+1,这也就是pushup函数中，求tr[u].len = b[tr[u].r + 1] - b[tr[u].l]的原因。

考虑把线段树每个节点u对应的区间(tr[u].l,tr[u].r)不变，改变区间和竖边的映射关系，

具体为： 节点u对应[b[tr[u].l],b[tr[u].r+1]]这条竖边。可以看到，这里很机智地把右端点的对应关系给改了下，于是就兼容了。

Q3:再详细解释一下为什么需要离散化？

答：离散化:将一个数轴上的一个一个点通过大小排序，保留点与点的大小关系

这道题目的线段树是绝对不会允许你开四倍于线段长度的(4e9)，百分百爆掉，这个时候就需要进行离散化，

离散化的原因是： 线段树的长度不能开的太大

Q4:本题明明是区间修改，为什么没有使用lazy标记，而是只有上传，没看到下传？

答：这与扫描线求并面积的需求相关，每次的查询操作都是查询整个区间，没有查询子区间的需求，所以只需要考虑上传，不用下传。

Q5:我看网上有题解的离散化没有使用二分查找(l,r),而是直接用的(L,R)，是怎么做到的，哪种更好些？

答： 真实数据：y_1,y_2<=1e9，简称为L,R 线段线中的节点4e5,简称为l,r

X:离散化数组 X[2*i-1]=L,X[2*i]=R 其中数组索引是线段树中节点的号，值为真实数据。

nmodify时，直接传入的是(L,R) 按理说应该找到对应的(l,r)，这样更直白，更清楚，办法就是：

int L = lower_bound(b + 1, b + tot + 1, line[i].y1) - b;
int R = lower_bound(b + 1, b + tot + 1, line[i].y2) - b;
R--;

注：上面的L,R是指线段树中的节点。 而网上的题解，并没有这个步骤，而是直接传入了原始数据， 然后利用递归+判断的办法来寻找合适的(l,r) 即:

if(X[r + 1] <= L || R <= X[l])		return;
if(L <= X[l] && X[r + 1] <= R) {
		tree[x].sum += c;
		pushup(x);
		return;
}

说白了，就是利用离散化数组X[]已经存储的信息，再加上递归，再加上判断，来衡量现在的区间[l,r]是否与现实中想要找的区间吻合，性能是一样的。

我还是推荐用传统的离散化+二分的办法来实现，套路清晰，modify代码基本就是模板形式，不像这种传入原始值的办法，还需要思考如何判断，把关键问题后移，反正我是不喜欢。

三、实现代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10; // 1e5个矩形
LL res;                 // 结果
int n;                  // n个矩形
int b[N << 2];          // 离散化数组,因为1e5个矩形，2e5条边，每条边两个y1,y2,所以，需要4e5

// 从左到右的扫描线
struct ScanLine {
    // y1,y2:这条线段上面的那个点和下面的那个点的y坐标
    // x:在这里不会用到，只是用来排序而已
    // k:是入边还是出边
    int y1, y2, x, mark;
    const bool operator<(const ScanLine &t) {
        return x < t.x; // 以x坐标进行排序
    }
} line[N << 1]; // 2e5条边

struct Node {
    int l, r;
    int len;  // 统计值：有效长度和
    int cnt;  // 属性：入边：+1，出边:-1,被多少个方格覆盖:cnt
} tr[N << 4]; // 开了16倍空间,矩形数量1e5,每个矩形2条竖边，就是2e5,每条边两个y1,y2,就是4e5个点，对于4e5需要开4倍空间，就是16e5

void pushup(int u) {
    // pushup：利用左右儿子的信息，更新u节点的统计信息
    //  扫描线题目中，统计信息就是有效区间长度，即len
    //  cnt不是统计信息，它可以视为某条线段树中某个区间的固有属性，它不需要进行向上推送更新

    // 整个区间被覆盖过，有效len等于区间长度
    // tr[u].l = L , tr[u].r + 1 =  R => 坐标系中的L,R与线段树中[l,r]之间的映射关系
    // 使用b[]离散数组，通过索引号找出此位置上的原始值，即y2,y1
    if (tr[u].cnt)
        tr[u].len = b[tr[u].r + 1] - b[tr[u].l];
    else
        tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
    // u节点所管辖的范围，并非完整命中，有效区间长度len=左节点len+右节点len
}

// 建树
void build(int u, int l, int r) {
    tr[u].l = l, tr[u].r = r;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
}

void modify(int u, int l, int r, int v) { // v:入边+1，出边-1
    if (l <= tr[u].l && r >= tr[u].r) {   // 如果完整区间命中
        tr[u].cnt += v;                   // 区间被覆盖次数+v
        pushup(u);                        // 属性的更改，会造成统计信息的变更,所以需要pushup
        return;
    }
    // 未完整命中时,分裂
    int mid = (tr[u].l + tr[u].r) >> 1;
    if (l <= mid) modify(u << 1, l, r, v);
    if (r > mid) modify(u << 1 | 1, l, r, v);
    // 更新统计信息
    pushup(u);
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("P5490.in", "r", stdin);
#endif
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);

    cin >> n;
    int x1, x2, y1, y2;
    for (int i = 1; i <= n; i++) {
        cin >> x1 >> y1 >> x2 >> y2;
        b[i * 2 - 1] = y1;
        b[i * 2] = y2;
        // 将y1,y2打入b数组，使得1e9的范围离散化,扫描线从左向右
        // 这里可以利用线段两个端点的特性，一个是2*i-1,另一个是2*i
        // 当然也可以使用游标的办法:++bl,效果是一样的，只要是保证能塞进离散化数组b就行

        // 将每个矩形的两条竖边记录扫描线数组
        // 一个竖着的线段，三个属性：y1,y2,x
        line[i * 2 - 1] = {y1, y2, x1, 1}; // 1:入边
        line[i * 2] = {y1, y2, x2, -1};    // -1:出边
    }

    n *= 2;                       // 一个矩形两条线段,直接乘2，方便后的计算,n的新含义：扫描线条数
    sort(line + 1, line + n + 1); // 按x坐标由小到大排序

    sort(b + 1, b + n + 1);                     // 将y坐标离散化
    int tot = unique(b + 1, b + n + 1) - b - 1; // 去重操作计算有多少个不同的y，也就是这个图象有几个y

    build(1, 1, tot - 1); // 建树
    /*
    Q:为什么是tot-1呢？
    答：因为[1,3][3,5]是坐标系中两条线段，但它们之间有交集3,采用的办法是左闭右开，即[1,3),[3,5)
    也就是{1,2},{3,4}共四个子矩形,看明白了吧，这个矩形是格子，相当于最多到r-1。
    最后一个右端点是tot,那么对应的线段数量就是tot-1
    */

    for (int i = 1; i < n; i++) { // 开始扫描，面积并中扫描到n-1条线段即可,最后一条没用
        int L = lower_bound(b + 1, b + tot + 1, line[i].y1) - b;
        int R = lower_bound(b + 1, b + tot + 1, line[i].y2) - b;
        // 在排好序并去重后的数组b中，通过二分+原始值y1,查找到y1在离散化后数组b的位置，位置编号就是y1在整体中的相当名次
        // 上面构建build时，也是用tot-1可丁可卯的大小创建的线段树，所以这里也必须用find后的位置编号去指定位置上修改

        modify(1, L, R - 1, line[i].mark);
        // y1,y2:坐标系中的真实值
        // L,R:离散化后的一一映射值
        // 上面已经讨论过，坐标系中的线段区间 与 线段树中管控范围不是一一对应的，线段树区间是左闭右开的
        // [L,R-1]-->(l,r)

        res += (LL)tr[1].len * (line[i + 1].x - line[i].x);
        // tr[1].len: 当前整体线段树中的可用长度和
        // line[i + 1].x - line[i].x :下一条扫描线与本扫描线之间的宽度(扫描线从左向右，x上的变化视为宽度)
        // res+ : 长度和*宽度
    }
    // 输出res
    printf("%lld\n", res);
    return 0;
}