|
|
##[$P4344$ [$SHOI2015$] 脑洞治疗仪](https://www.luogu.com.cn/problem/P4344)
|
|
|
|
|
|
### 一、题目描述
|
|
|
|
|
|
曾经发明了自动刷题机的发明家 $SHTSC$ 又公开了他的新发明:脑洞治疗仪——一种可以治疗他因为发明而日益增大的脑洞的神秘装置。
|
|
|
|
|
|
为了简单起见,我们将大脑视作一个 $01$ 序列。$1$ 代表这个位置的脑组织正常工作,$0$ 代表这是一块脑洞。
|
|
|
|
|
|
```cpp
|
|
|
1 0 1 0 0 0 1 1 1 0
|
|
|
```
|
|
|
|
|
|
脑洞治疗仪修补某一块脑洞的基本工作原理就是将另一块连续区域挖出,**将其中正常工作的脑组织填补在这块脑洞中**。(所以脑洞治疗仪是脑洞的治疗仪?)
|
|
|
|
|
|
例如,用上面第 $8$ 号位置到第 $10$ 号位置去修补第 $1$ 号位置到第 $4$ 号位置的脑洞,我们就会得到:
|
|
|
|
|
|
```cpp
|
|
|
1 1 1 1 0 0 1 0 0 0
|
|
|
```
|
|
|
|
|
|
如果再用第 $1$ 号位置到第 $4$ 号位置去修补第 $8$ 号位置到第 $10$ 号位置:
|
|
|
|
|
|
```cpp
|
|
|
0 0 0 0 0 0 1 1 1 1
|
|
|
```
|
|
|
|
|
|
这是因为脑洞治疗仪 **会把多余出来的脑组织直接扔掉**。
|
|
|
|
|
|
如果再用第 $7$ 号位置到第 $10$ 号位置去填补第 $1$ 号位置到第 $6$ 号位置:
|
|
|
|
|
|
```cpp
|
|
|
1 1 1 1 0 0 0 0 0 0
|
|
|
```
|
|
|
|
|
|
这是因为如果新脑洞挖出来的脑组织不够多,**脑洞治疗仪仅会尽量填补位置比较靠前的脑洞**。
|
|
|
|
|
|
假定初始时 $SHTSC$ 并没有脑洞,给出一些挖脑洞和脑洞治疗的操作序列,你需要即时回答 $SHTSC$ 的问题:**在大脑某个区间中最大的连续脑洞区域有多大**。
|
|
|
|
|
|
#### 输入格式
|
|
|
|
|
|
第一行两个整数 $n,m$,表示 SHTSC 的大脑可分为从 $1$ 到 $n$ 编号的 $n$ 个连续区域,有 $m$ 个操作。
|
|
|
|
|
|
以下 $m$ 行每行是下列三种格式之一:
|
|
|
* $0\quad l\quad r$:SHTSC 挖了一个范围为 $[l, r]$ 的脑洞。
|
|
|
* $1\quad l_0\quad r_0\quad l_1\quad r_1$:SHTSC 进行了一次脑洞治疗,用从 $l_0$ 到 $r_0$ 的脑组织修补 $l_1$ 到 $r_1$ 的脑洞。
|
|
|
* $2\quad l\quad r$:SHTSC 询问 $[l, r]$ 区间内最大的脑洞有多大。
|
|
|
|
|
|
上述区间均在 $[1, n]$ 范围内。
|
|
|
|
|
|
#### 输出格式
|
|
|
|
|
|
对于每个询问,输出一行一个整数,表示询问区间内最大连续脑洞区域有多大。
|
|
|
|
|
|
#### 样例 #1
|
|
|
|
|
|
#### 样例输入 #1
|
|
|
|
|
|
```
|
|
|
10 10
|
|
|
0 2 2
|
|
|
0 4 6
|
|
|
0 10 10
|
|
|
2 1 10
|
|
|
1 8 10 1 4
|
|
|
2 1 10
|
|
|
1 1 4 8 10
|
|
|
2 1 10
|
|
|
1 7 10 1 6
|
|
|
2 1 10
|
|
|
```
|
|
|
|
|
|
#### 样例输出 #1
|
|
|
|
|
|
```
|
|
|
3
|
|
|
3
|
|
|
6
|
|
|
6
|
|
|
```
|
|
|
|
|
|
#### 提示
|
|
|
|
|
|
对于 $20\%$ 的数据,$n, m \leq 100$;
|
|
|
对于 $50\%$ 的数据,$n, m \leq 20000$;
|
|
|
对于 $100\%$ 的数据,$n, m \leq 200000$。
|
|
|
|
|
|
### 三、线段树解法
|
|
|
前言
|
|
|
这道题目呢,看上去很难,实际上我们可以用线段树解决这道题目。
|
|
|
|
|
|
我们维护 $sum、len、tag、lmax、rmax、ans$。
|
|
|
|
|
|
- $sum$: 区间正常脑组织个数
|
|
|
- $len$: 区间长度
|
|
|
- $tag$: 懒标记
|
|
|
- $lmax$: 从左开始的连续脑洞个数
|
|
|
- $rmax$: 从右开始的连续脑洞个数
|
|
|
- $ans$: 区间最大的连续脑洞数量
|
|
|
|
|
|
#### 建树
|
|
|
由于 len 是不变的,所以我们可以建树的时候就求出 len
|
|
|
```cpp {.line-numbers}
|
|
|
tr[num].len=r-l+1;
|
|
|
```
|
|
|
|
|
|
#### $pushup$
|
|
|
`sum`
|
|
|
`sum` 就是左子树和右子树的 $sum$ 的和。
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
tr[u].sum=tr[ls].sum+tr[rs].sum;
|
|
|
```
|
|
|
|
|
|
#### $lmax$
|
|
|
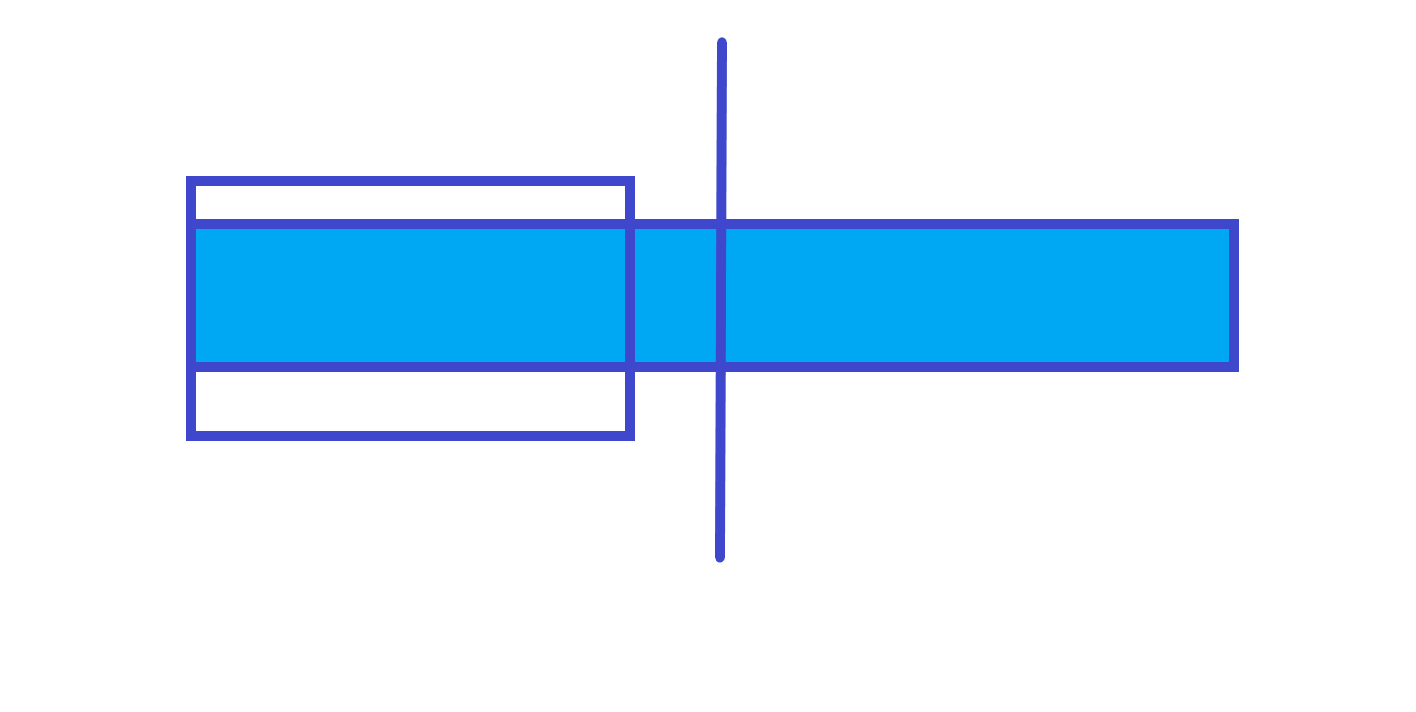
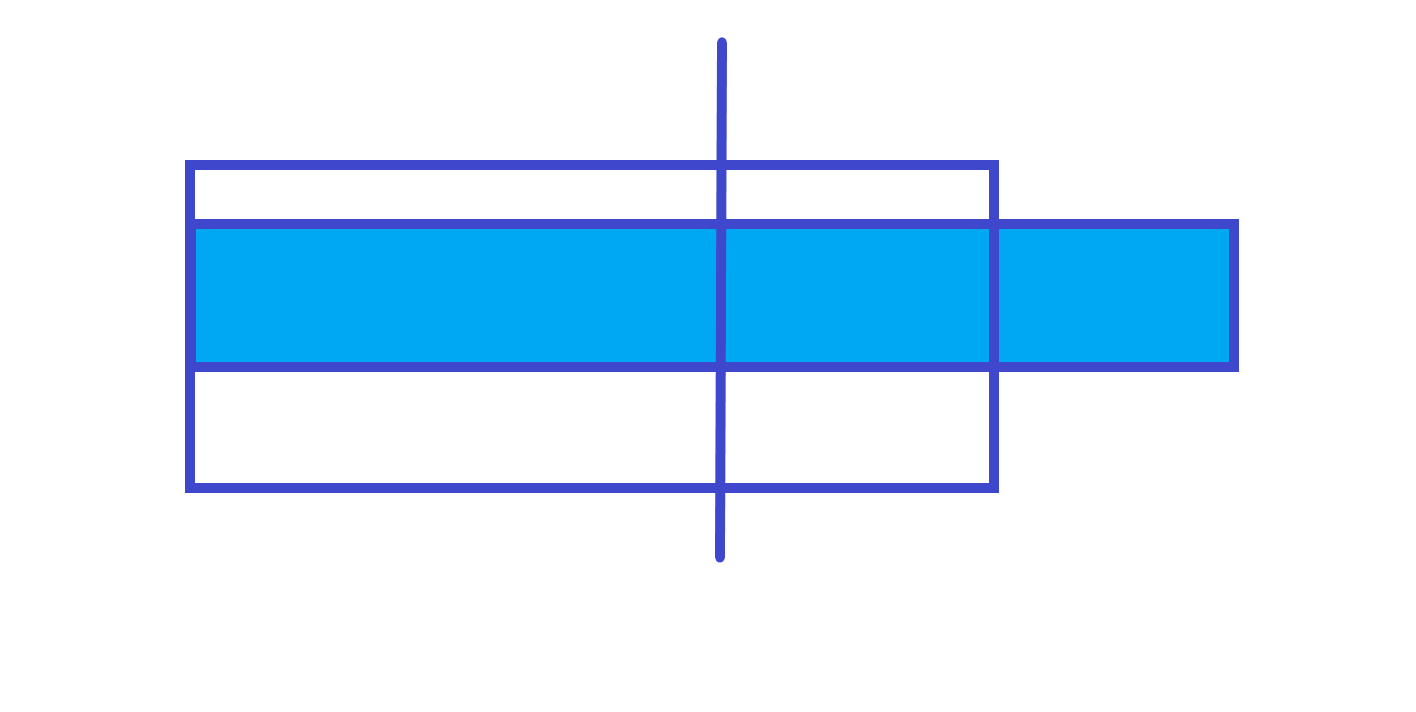
$lmax$ 的话有两种情况
|
|
|
|
|
|
第 $1$ 种情况
|
|
|
|
|
|
|
|
|
$lmax$=左子树的 $lmax$
|
|
|
|
|
|
第 $2$ 种情况
|
|
|
|
|
|
|
|
|
$lmax$=左子树的 $len$ + 右子树的 $lmax$
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
if(tr[ls].lmax==tr[ls].len) tr[u].lmax=tr[ls].len+tr[rs].lmax;
|
|
|
else tr[u].lmax=tr[ls].lmax;
|
|
|
```
|
|
|
#### $rmax$
|
|
|
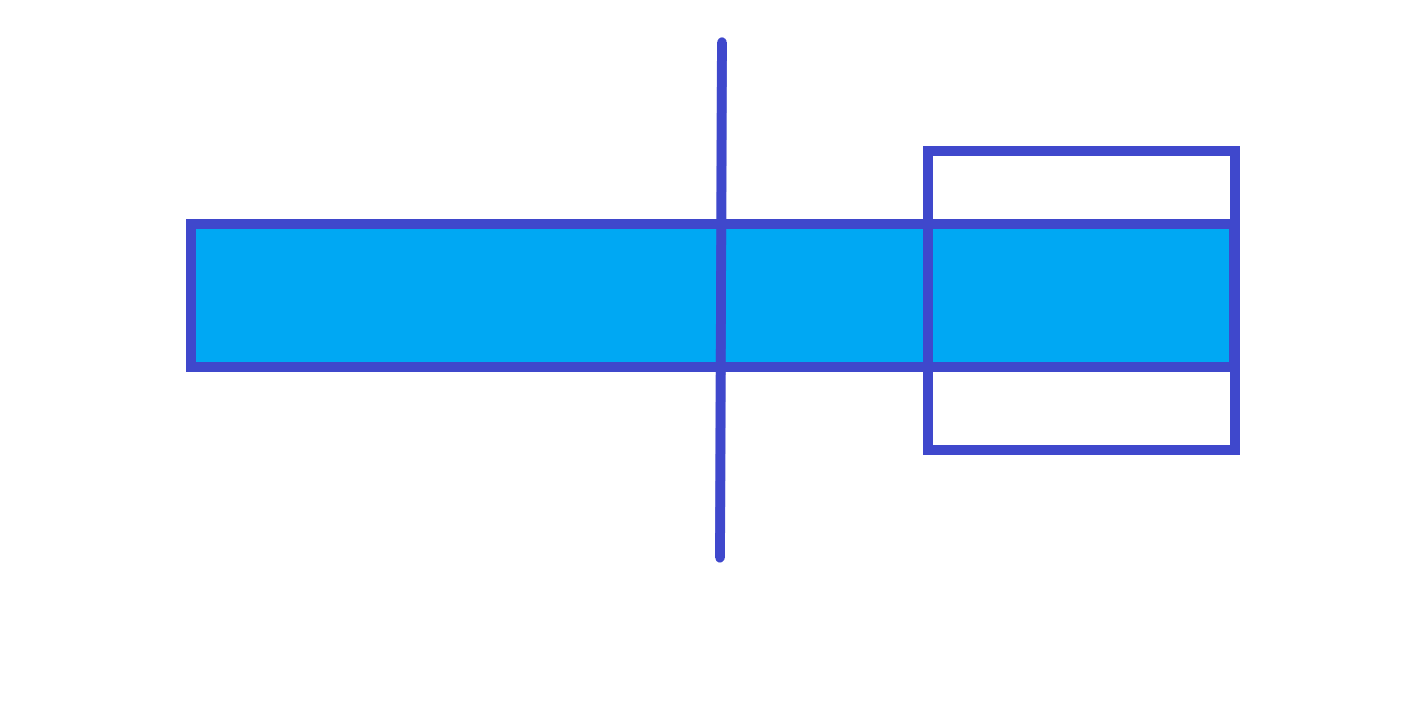
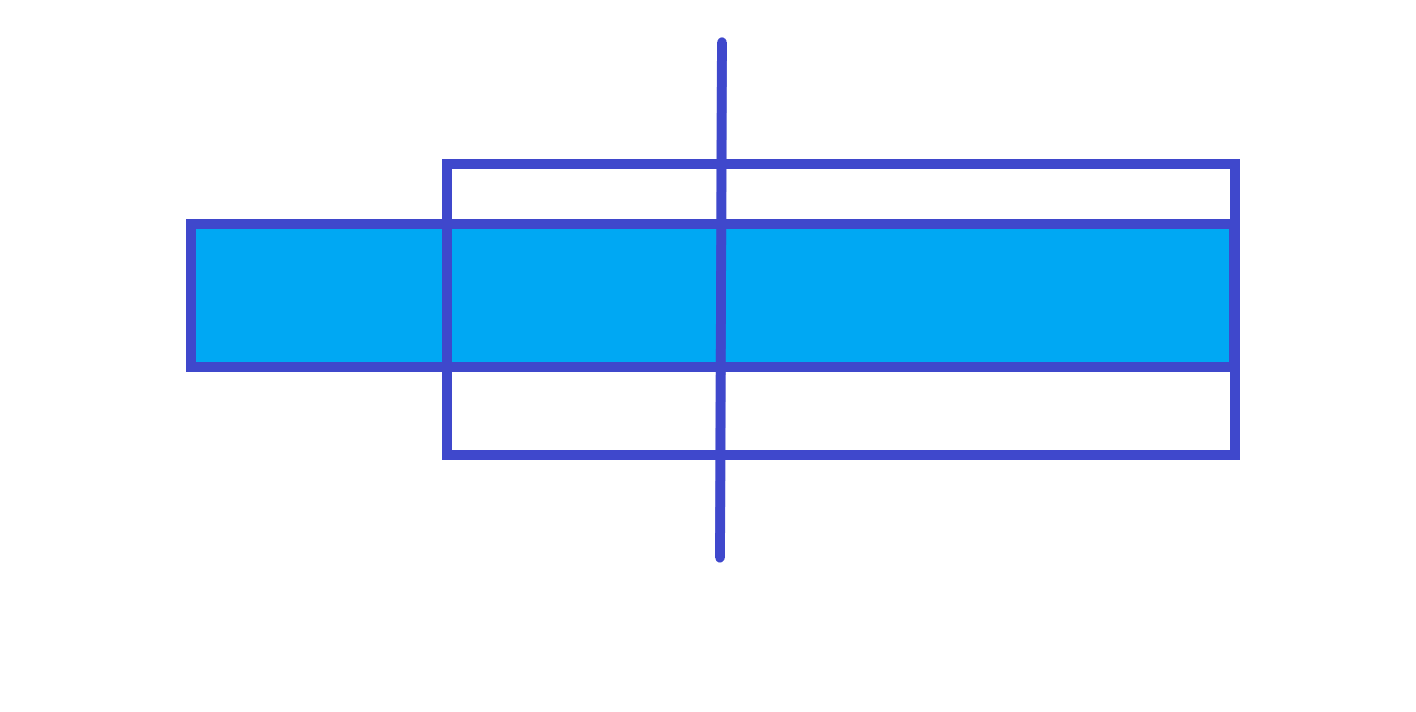
$rmax$ 的话也两种情况
|
|
|
|
|
|
第 $1$ 种情况
|
|
|
|
|
|
|
|
|
$rmax$=右子树的 $rmax$
|
|
|
|
|
|
|
|
|
|
|
|
$lmax$=右子树的 $len$ + 左子树的 $rmax$
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
if(tr[rs].rmax==tr[rs].len)tr[u].rmax=tr[rs].len+tr[ls].rmax;
|
|
|
else tr[u].rmax=tr[rs].rmax;
|
|
|
```
|
|
|
|
|
|
#### $ans$
|
|
|
$ans$ 的话有 $3$ 种情况
|
|
|
|
|
|
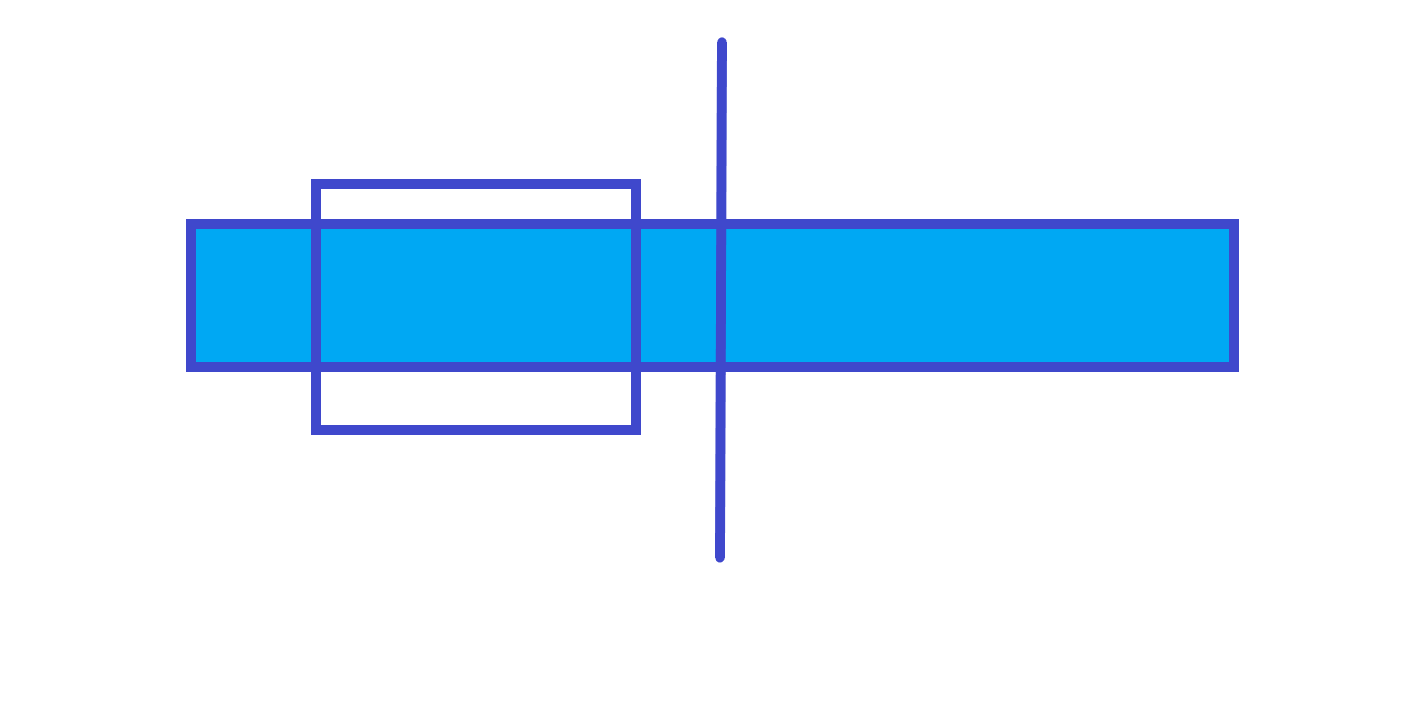
第 $1$ 种情况
|
|
|
|
|
|
|
|
|
$ans$=左子树的 $ans$
|
|
|
|
|
|
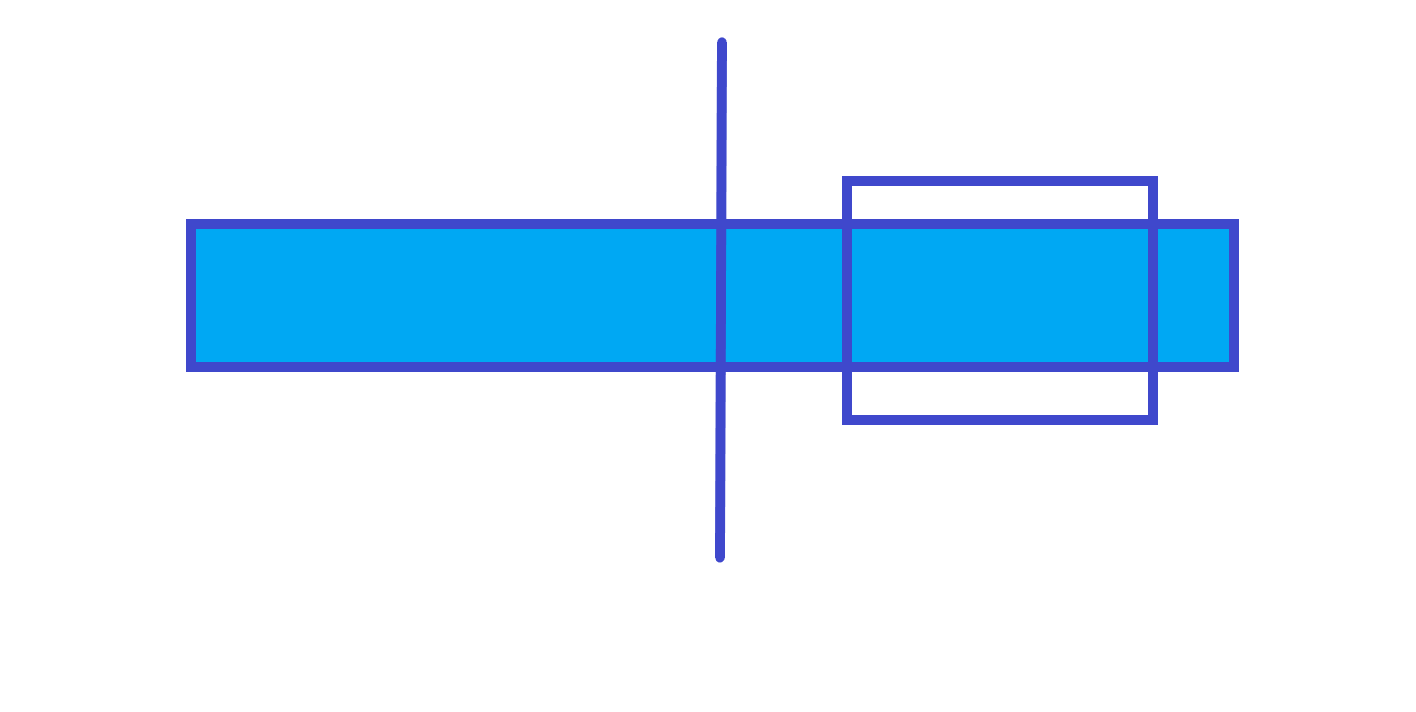
第 $2$ 种情况
|
|
|
|
|
|
|
|
|
$ans$=右子树的 $ans$
|
|
|
|
|
|
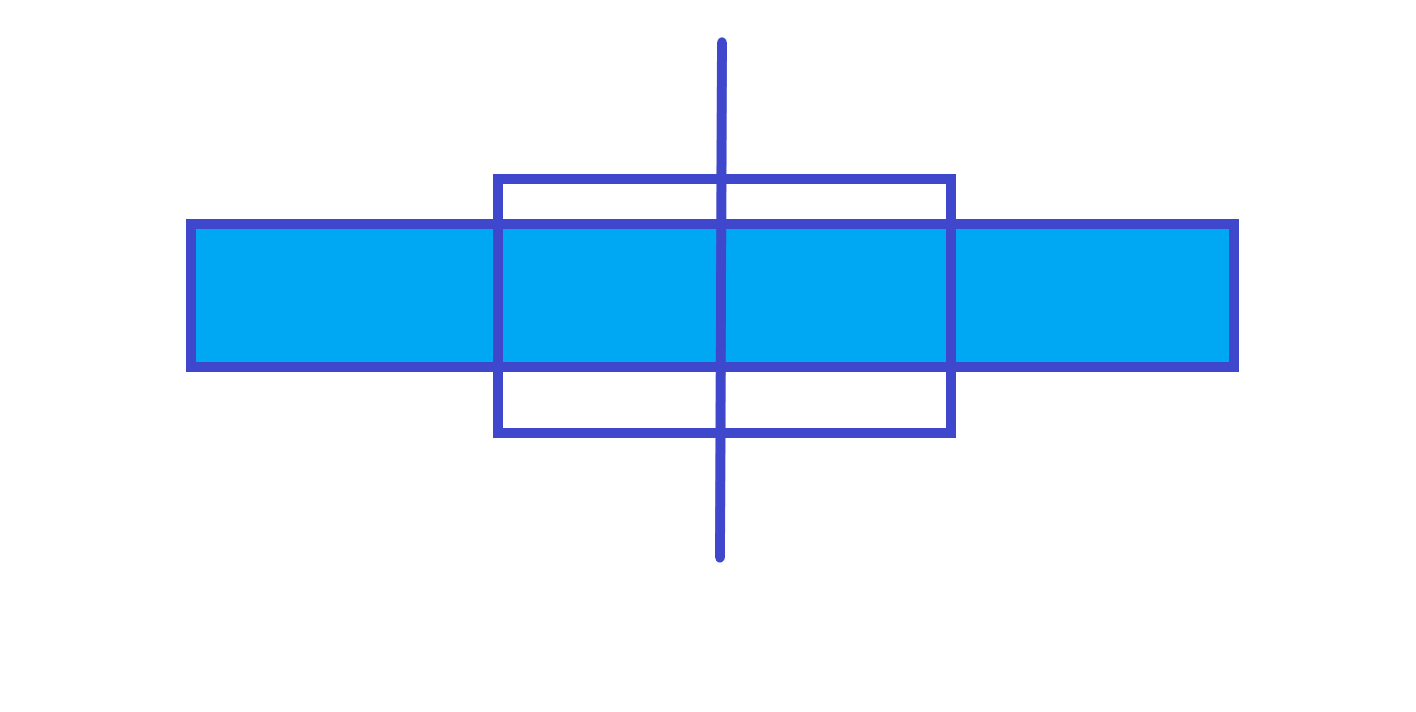
第 $3$ 种情况
|
|
|
|
|
|
|
|
|
$ans$=左子树的$rmax$ + 右子树的$lmax$
|
|
|
```cpp {.line-numbers}
|
|
|
tr[u].ans=max(max(t[ls].ans,t[rs].ans),t[ls].rmax+t[rs].lmax);
|
|
|
```
|
|
|
|
|
|
答案在左右的交界处 : $tr[ls].rmax+tr[rs].lmax$
|
|
|
|
|
|
><font color='red' size=4><b>注意</b></font>
|
|
|
这里需要特别注意,因为$tr[ls].rmax$的长度和$tr[rs].lmax$的长度可能会超过$[L,R]$的范围,如果超过,就只能截取一部分。
|
|
|
|
|
|
- 左儿子区间长度 = $tr[rs].l - L$
|
|
|
- 右儿子区间长度 = $R - tr[ls].r$
|
|
|
|
|
|
代码
|
|
|
`min(tr[ls].rmax, tr[rs].l - L) + min(tr[rs].lmax, R - tr[ls].r))`
|
|
|
|
|
|
就可以保证只截取有效范围内的连续数字0的个数啦~
|
|
|
|
|
|
><font color='red' size=4><b>总结</b></font>
|
|
|
我一开始看这个非常清晰的代码时,一时脑袋短路,没看懂,以为就是
|
|
|
$query2(ls,L,R)+query2(rs,L,R)$
|
|
|
|
|
|
结果大量的$WA$。理解不了的时候,就去找别的题解看了,现在想来就是在浪费时间,还是需要沉下心来,仔细理解,少走弯路。
|
|
|
|
|
|
|
|
|
#### $pushdown$
|
|
|
`tag`
|
|
|
|
|
|
我们的 `tag` 有 $3$ 种值,分别为 $-1,0,1$
|
|
|
|
|
|
$-1$ : 默认值
|
|
|
|
|
|
$0$ : 区间内全部修改为0
|
|
|
|
|
|
$1$ : 区间内全部修改为1
|
|
|
|
|
|
$-1$ 的话: 代表没有任何操作,不要管。
|
|
|
|
|
|
$0$ 的话:
|
|
|
|
|
|
我们对照上面的发现:
|
|
|
|
|
|
$ans$、$lmax$、$rmax$ 都为 $len$。
|
|
|
|
|
|
而 $sum$ 则为 $0$
|
|
|
|
|
|
$1$ 的话:
|
|
|
我们对照上面的发现:
|
|
|
|
|
|
$ans、lmax、rmax$ 都为 $0$。
|
|
|
|
|
|
而 $sum$ 则为 $len$。
|
|
|
|
|
|
**代码**
|
|
|
```cpp {.line-numbers}
|
|
|
void change(int u, int tag) {
|
|
|
if (tag == 0) {
|
|
|
tr[u].ans = tr[u].lmax = tr[u].rmax = tr[u].len;
|
|
|
tr[u].sum = 0;
|
|
|
}
|
|
|
if (tag == 1) {
|
|
|
tr[u].ans = tr[u].lmax = tr[u].rmax = 0;
|
|
|
tr[u].sum = tr[u].len;
|
|
|
}
|
|
|
// 记录当前区间的懒标记,以后可以向下进行传递
|
|
|
tr[u].tag = tag;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
#### 二分
|
|
|
我们可以发现,操作 $2$ 就是先统计一遍 $[l_1,r_1]$ 中数字$1$的个数。
|
|
|
然后把 $[l_1,r_1]$ 这段区间全部变成$0$,再去在$[l_2,r_2]$ 这段区间里找到从$l_2$ 开始算起最右边脑洞个数 ≤$[l_1,r_1]$ 中脑洞的个数。
|
|
|
|
|
|
我们发现脑洞个数是单调递增的,所以我们可以 **二分**。
|
|
|
|
|
|
#### 复杂度 $O(nlogn+qlog^2 n)$
|
|
|
|
|
|
#### $Code$
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
const int N = 2e5 + 10;
|
|
|
|
|
|
int n, m, l1, r1, l2, r2;
|
|
|
|
|
|
// 线段树维护区间最大连续子序列和
|
|
|
#define ls u << 1
|
|
|
#define rs u << 1 | 1
|
|
|
struct Node {
|
|
|
int l, r;
|
|
|
int lmax, rmax; // 从左开始的连续脑洞个数,从右开始的连续脑洞个数
|
|
|
int sum; // 区间正常脑组织个数
|
|
|
int len; // 区间长度
|
|
|
int ans; // 区间最大的连续脑洞数量
|
|
|
int tag; // 懒标记
|
|
|
} tr[N << 2];
|
|
|
|
|
|
void pushup(int u) {
|
|
|
tr[u].sum = tr[ls].sum + tr[rs].sum; // 区间正常脑组织个数
|
|
|
|
|
|
if (tr[ls].lmax == tr[ls].len) // 左边都是0
|
|
|
tr[u].lmax = tr[ls].len + tr[rs].lmax; // 父亲左最长=左子整个长+右子树左最长
|
|
|
else
|
|
|
tr[u].lmax = tr[ls].lmax;
|
|
|
|
|
|
if (tr[rs].rmax == tr[rs].len) // 右边都是0
|
|
|
tr[u].rmax = tr[rs].len + tr[ls].rmax; // 父亲右最长=右子整个长+左子树右最长
|
|
|
else
|
|
|
tr[u].rmax = tr[rs].rmax;
|
|
|
|
|
|
// 三种情况,分情况讨论
|
|
|
tr[u].ans = max({tr[ls].ans, tr[rs].ans, tr[ls].rmax + tr[rs].lmax});
|
|
|
}
|
|
|
|
|
|
void build(int u, int l, int r) {
|
|
|
tr[u].l = l, tr[u].r = r, tr[u].tag = -1; // 边界,懒标记初始化
|
|
|
tr[u].len = r - l + 1; // 区间长度,虽然记录了l,r,也可以现用现算,但一次计算还是代码更短,但内存会更大
|
|
|
if (l == r) {
|
|
|
tr[u].sum = 1; // 初始化时,是没有脑洞的,都是正常的脑组织
|
|
|
tr[u].ans = tr[u].lmax = tr[u].rmax = 0; // 因为默认值是1,所以不写也行,但好习惯是写就写全,不用默认值
|
|
|
/* ans 区间最大的连续脑洞数量 = 0
|
|
|
lmax 从左开始的连续脑洞个数 = 0
|
|
|
rmax 从右开始的连续脑洞个数 = 0
|
|
|
*/
|
|
|
return;
|
|
|
}
|
|
|
int mid = (l + r) >> 1;
|
|
|
build(ls, l, mid), build(rs, mid + 1, r);
|
|
|
pushup(u);
|
|
|
}
|
|
|
|
|
|
/* 功能:在u节点管控的区间完整命中的情况下,更新u节点的统计信息,并且变更u节点的懒标记为tag
|
|
|
Q:为什么要独立封装出来一个chang函数,我看其它线段树的题目中没有这个东西?
|
|
|
答:在有懒标记的区间修改题目中,会在三个地方使用到修改u管辖范围内的统计信息、记录懒标识的情况:
|
|
|
① modify中完整命中时,对于整体区间需要修改统计信息和下传懒标记
|
|
|
② 分裂pushdown时,如果u区间存在懒标记,需要同时修改左、右儿子的统计信息和懒标记
|
|
|
如此说来,这个change(u,tag)独立封装出来就完全合理了,因为可以复用,功能就是将当前节点的管辖区间修改统计信息和懒标记
|
|
|
这个change(u,tag)应该对于每个需要下传懒标记的线段树都是一样有用的,只不过有的逻辑太简单,一句话两句话就直接在modify、
|
|
|
pushdown里实现了,没有独立封成change(u,tag)函数,按道理来讲,其实全都封成change函数才上正道。
|
|
|
*/
|
|
|
void change(int u, int tag) {
|
|
|
// 根据懒标记的不同,结合业务逻辑,对于u管辖的区间进行统计信息的变更(tr[u].len不需要变更,它不是统计信息,它是属性)
|
|
|
// ① 单个懒标记:不同的数值表示不同的含义,处理逻辑不同,比如本题 √
|
|
|
// ② 单个懒标记:不同的数值表示相同的含义,处理逻辑相同,比如都是+tag
|
|
|
// ③ 多个懒标记:不同的tag代表不同的业务逻辑
|
|
|
if (tag == 0) {
|
|
|
tr[u].ans = tr[u].lmax = tr[u].rmax = tr[u].len;
|
|
|
tr[u].sum = 0;
|
|
|
}
|
|
|
if (tag == 1) {
|
|
|
tr[u].ans = tr[u].lmax = tr[u].rmax = 0;
|
|
|
tr[u].sum = tr[u].len;
|
|
|
}
|
|
|
// 记录当前区间的懒标记,以后可以向下进行传递
|
|
|
tr[u].tag = tag;
|
|
|
}
|
|
|
|
|
|
// 下传懒标记,让左右儿子进行统计信息修改和懒标记修改
|
|
|
void pushdown(int u) {
|
|
|
if (~tr[u].tag) {
|
|
|
// 递归处理左右子树
|
|
|
change(ls, tr[u].tag), change(rs, tr[u].tag);
|
|
|
// 下传完毕,懒标记清空
|
|
|
tr[u].tag = -1;
|
|
|
}
|
|
|
}
|
|
|
|
|
|
// 将区间[L,R]修改为v
|
|
|
void modify(int u, int L, int R, int v) {
|
|
|
int l = tr[u].l, r = tr[u].r;
|
|
|
if (l >= L && r <= R) { // 如果完整命中,那么根据修改的值,对于整体区间的统计信息进行计算,同时,对于整体区间打加修改的懒标记v
|
|
|
change(u, v);
|
|
|
return;
|
|
|
}
|
|
|
if (l > R || r < L) return; // 如果与当前区间无交集,那么返回
|
|
|
|
|
|
// 下传懒标记
|
|
|
pushdown(u);
|
|
|
// 分裂
|
|
|
modify(ls, L, R, v), modify(rs, L, R, v);
|
|
|
// 向上汇总信息
|
|
|
pushup(u);
|
|
|
}
|
|
|
|
|
|
// 查询区间内数字0的个数
|
|
|
int query0(int u, int L, int R) {
|
|
|
int l = tr[u].l, r = tr[u].r;
|
|
|
if (l >= L && r <= R) return tr[u].len - tr[u].sum;
|
|
|
if (l > R || r < L) return 0;
|
|
|
pushdown(u);
|
|
|
return query0(ls, L, R) + query0(rs, L, R);
|
|
|
}
|
|
|
|
|
|
// 查询区间内数字1的个数
|
|
|
int query1(int u, int L, int R) {
|
|
|
int l = tr[u].l, r = tr[u].r;
|
|
|
if (l >= L && r <= R) return tr[u].sum;
|
|
|
if (l > R || r < L) return 0;
|
|
|
pushdown(u);
|
|
|
return query1(ls, L, R) + query1(rs, L, R);
|
|
|
}
|
|
|
|
|
|
// 查询区间内连续数字0的长度
|
|
|
int query2(int u, int L, int R) {
|
|
|
int l = tr[u].l, r = tr[u].r;
|
|
|
if (l >= L && r <= R) return tr[u].ans; // 区间最大的连续脑洞数量
|
|
|
if (l > R || r < L) return 0;
|
|
|
|
|
|
pushdown(u);
|
|
|
/*三种情况:
|
|
|
1、答案在左半边 : query2(ls, L, R)
|
|
|
2、答案在右半边 : query2(rs, L, R)
|
|
|
3、左半边的后面+右半边的前面(不能越界)
|
|
|
*/
|
|
|
return max({query2(ls, L, R), query2(rs, L, R), min(tr[ls].rmax, tr[rs].l - L) + min(tr[rs].lmax, R - tr[ls].r)});
|
|
|
}
|
|
|
|
|
|
// 操作2
|
|
|
void solve() {
|
|
|
cin >> l2 >> r2;
|
|
|
int sum = query1(1, l1, r1); // 数字1的个数
|
|
|
if (sum == 0) return; // 特判,如果没有数字1,就没有继续的必要了:你准备用一个区间里的1去填充别人家的空闲区域,结果,你一个都没有,那还填什么填
|
|
|
|
|
|
// 将区[l1,r1]所有位置修改为0,把所有数字1都取走
|
|
|
modify(1, l1, r1, 0);
|
|
|
/*
|
|
|
注意:懒标记=-1,默认值;懒标记=0,修改为0;懒标记=1,修改为1;
|
|
|
这里需要注意把懒标记在build时初始化为-1,否则,如果懒标记默认值是0,这里还需要将位置修改为0就有二义性了,
|
|
|
你就不知道一个tag=0到底是啥意思,是初始值没有修改过,还是修改过变成了0了? 初始化为-1是一下好习惯,以后要全面执行这个规则。
|
|
|
|
|
|
因为需要进行推平操作,我们知道左侧肯定是l2,那么,右侧到哪里结束呢?
|
|
|
因为[l2,r2]中可能有的位置是0,有的位置是1 ,我们现在有sum个1,假设最后的右端点位置是x, 那么执行推平操作后,
|
|
|
则[l2,x]必然都是1。
|
|
|
问题是如何找到这个右端点x呢?当然可以暴力,一个个找过去,发现是1就放过,发现是0就计数,然后一旦计数到达sum,就是找到了合适的位置x,
|
|
|
还有更聪明的办法,就是二分,因为这个一个个找过去的办法具有单调性,我们如果合理使用查找数字0的函数query0,获取指定区间[l2,x]范围内数
|
|
|
字0的个数,找出x的具体位置,然后再执行一下modify(1,l2,x,1)即可
|
|
|
*/
|
|
|
int l = l2, r = r2;
|
|
|
while (l < r) {
|
|
|
int mid = (l + r) >> 1;
|
|
|
if (query0(1, l2, mid) >= sum) // 在以root=1的树中,[l2,mid]这个区间内,查找数字0的个数,如果左边的0位置数量多于sum,则只用递归左侧即可
|
|
|
r = mid;
|
|
|
else
|
|
|
l = mid + 1;
|
|
|
}
|
|
|
modify(1, l2, l, 1);
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
#ifndef ONLINE_JUDGE
|
|
|
freopen("P4344.in", "r", stdin);
|
|
|
#endif
|
|
|
// 加快读入
|
|
|
ios::sync_with_stdio(false), cin.tie(0);
|
|
|
cin >> n >> m;
|
|
|
// 构建线段树
|
|
|
build(1, 1, n);
|
|
|
|
|
|
int op;
|
|
|
while (m--) {
|
|
|
cin >> op >> l1 >> r1;
|
|
|
if (op == 0) modify(1, l1, r1, 0); // SHTSC 挖了一个范围为 [l, r]的脑洞。
|
|
|
if (op == 1) solve(); // 把操作2封装成一个solve()函数,可以更好的理清代码的逻辑
|
|
|
if (op == 2) cout << (query2(1, l1, r1)) << endl; // 连续数字0的最大长度
|
|
|
}
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
|
|
|
### 三、柯朵莉树解法
|
|
|
【~~骗分,时间复杂度不达标~~】
|
|
|
|
|
|
三种操作:
|
|
|
|
|
|
- 区间赋值为 $0$
|
|
|
|
|
|
- 取出一个区间的 $1$ 修补另一个区间的 $0$
|
|
|
|
|
|
- 查询区间内最长的连续 $1$ 的长度。
|
|
|
|
|
|
对于操作一就是 $ODT$ 的基本操作,直接赋值。
|
|
|
|
|
|
对于操作二,我们直接统计第一个区间内 $0$ 的个数,然后再遍历第二个区间直接赋值。
|
|
|
|
|
|
对于操作三,我们直接暴力统计就好。
|
|
|
#### $Code$
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
#define int long long
|
|
|
#define N 1000100
|
|
|
|
|
|
// 柯朵莉树
|
|
|
// O2优化后,也过不去最后的两个测试点TLE
|
|
|
int n, m;
|
|
|
struct Node {
|
|
|
int l, r;
|
|
|
mutable int v;
|
|
|
Node(int L, int R = 0, int V = 0) :
|
|
|
l(L), r(R), v(V) {
|
|
|
}
|
|
|
bool operator<(const Node &t) const {
|
|
|
return l < t.l;
|
|
|
}
|
|
|
};
|
|
|
set<Node> s;
|
|
|
|
|
|
set<Node>::iterator split(int p) {
|
|
|
auto it = s.lower_bound(Node(p));
|
|
|
if (it != s.end() && it->l == p) return it;
|
|
|
it--;
|
|
|
int l = it->l, r = it->r, v = it->v;
|
|
|
s.erase(it);
|
|
|
s.insert(Node(l, p - 1, v));
|
|
|
return s.insert(Node(p, r, v)).first;
|
|
|
}
|
|
|
|
|
|
void assign(int l, int r, int v) {
|
|
|
auto R = split(r + 1), L = split(l);
|
|
|
s.erase(L, R);
|
|
|
s.insert(Node(l, r, v));
|
|
|
}
|
|
|
|
|
|
// 本题逻辑,区间修改[l1,r1]--->[l2,r2]
|
|
|
void change(int l1, int r1, int l2, int r2) {
|
|
|
int res = 0;
|
|
|
auto R = split(r1 + 1), L = split(l1), it = L;
|
|
|
for (; L != R; L++)
|
|
|
if (L->v == 1) res += (L->r - L->l + 1); // 记录正常脑组织的个数
|
|
|
|
|
|
s.erase(it, R); // 删除旧区间
|
|
|
s.insert(Node(l1, r1, 0)); // 旧区间清零
|
|
|
|
|
|
if (!res) return; // 如果这里面没有正常脑组织,那还修什么修
|
|
|
|
|
|
R = split(r2 + 1), L = split(l2), it = L;
|
|
|
|
|
|
// 个人理解属于优化,事实也是如此,但优化后效果是一样的,还是挂了两个测试点TLE
|
|
|
// if (res >= r2 - l2 + 1) { // 如果正常脑组织的个数,超过预修补区间的长度,那么多余的扔掉
|
|
|
// s.erase(L, R);
|
|
|
// s.insert(Node(l2, r2, 1));
|
|
|
// return;
|
|
|
// }
|
|
|
|
|
|
// 小于等于目标区间长度
|
|
|
for (; L != R; L++) {
|
|
|
if (L->v == 0) {
|
|
|
res -= L->r - L->l + 1; // 利用正常的脑组织进行修补
|
|
|
if (res < 0) { // 如果正常脑组织放在这个区间不够
|
|
|
assign(L->l, L->r + res, 1); // 能修多少算多少
|
|
|
break; // 剩余的使没了,不用再往下查看了
|
|
|
} else
|
|
|
L->v = 1; // 暴力修改此区域的值v=1
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
|
|
|
int query(int l, int r) {
|
|
|
auto R = split(r + 1), L = split(l);
|
|
|
int res = 0, sum = 0;
|
|
|
for (; L != R; L++) {
|
|
|
if (L->v == 0) // 如果区间值为0,累加计算本轮可以获取到的最长连续0长度,准备参加PK大赛
|
|
|
sum += L->r - L->l + 1;
|
|
|
else
|
|
|
// 如果区间不为0,则以上一轮的最长的、区间内都是0的长度是多少
|
|
|
// 不断进行PK大赛,选举出最长的区间最大的连续脑洞区域
|
|
|
res = max(res, sum), sum = 0;
|
|
|
}
|
|
|
// 这里有技巧!一般我们直接返回res,但是这里不行,因为如果最后一块是连续的0,那么else的代码将无法执行,造成结果错误,需要最后补一下检查
|
|
|
return max(res, sum);
|
|
|
}
|
|
|
|
|
|
signed main() {
|
|
|
// 加快读入
|
|
|
ios::sync_with_stdio(false), cin.tie(0);
|
|
|
cin >> n >> m;
|
|
|
|
|
|
// 柯朵莉初始化
|
|
|
// 最初是没有脑洞的,全部是正常的大脑,都是1
|
|
|
s.insert(Node(1, n, 1));
|
|
|
|
|
|
while (m--) {
|
|
|
int op, l, r;
|
|
|
cin >> op >> l >> r;
|
|
|
if (op == 0) assign(l, r, 0); //[l,r]之间挖出脑洞
|
|
|
if (op == 1) { // 进行了一次脑洞治疗,从[l1,r1]--->[l2,r2]进行修补
|
|
|
int l2, r2;
|
|
|
cin >> l2 >> r2;
|
|
|
change(l, r, l2, r2);
|
|
|
}
|
|
|
// 询问 [l, r] 区间内最大的脑洞有多大.也就是有多少个0
|
|
|
if (op == 2) cout << query(l, r) << endl;
|
|
|
}
|
|
|
return 0;
|
|
|
}
|
|
|
```
|