You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
11 KiB
11 KiB
P3960 列队 NOIP2017 提高组
一、题目描述
Sylvia 是一个热爱学习的女孩子。
前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。
Sylvia 所在的方阵中有 n \times m 名学生，方阵的行数为 n，列数为 m。
为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中 的学生从 1 到 n \times m 编上了号码（参见后面的样例）。即：初始时，第 i 行第 j 列 的学生的编号是 (i-1)\times m + j。
然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天 中，一共发生了 q 件这样的离队事件。每一次离队事件可以用数对 (x,y) (1 \le x \le n, 1 \le y \le m) 描述，表示第 x 行第 y 列的学生离队。
在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达这样的两条指令：
- 向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条指令之后，空位在第
x行第m列。 - 向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条指令之后，空位在第
n行第m列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后， 下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第 n 行 第 m 列一个空位，这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊，所以 Sylvia 想要计算每一次离队事件中，离队的同学的编号是多少。
注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后方阵中同学的编号可能是乱序的。
输入格式
输入共 q+1 行。
第一行包含 3 个用空格分隔的正整数 n, m, q，表示方阵大小是 n 行 m 列，一共发生了 q 次事件。
接下来 q 行按照事件发生顺序描述了 q 件事件。每一行是两个整数 x, y，用一个空 格分隔，表示这个离队事件中离队的学生当时排在第 x 行第 y 列。
输出格式
按照事件输入的顺序，每一个事件输出一行一个整数，表示这个离队事件中离队学生的编号。
样例输入 #1
2 2 3
1 1
2 2
1 2
样例输出 #1
1
1
4
提示
【输入输出样例 1 说明】
\begin{matrix}
\begin{bmatrix}
1 & 2 \\
3 & 4 \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
& 2 \\
3 & 4 \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
2 & \\
3 & 4 \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
2 & 4 \\
3 & \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
2 & 4 \\
3 & 1 \\
\end{bmatrix} \\[1em]
\begin{bmatrix}
2 & 4 \\
3 & 1 \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
2 & 4 \\
3 & \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
2 & 4 \\
3 & \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
2 & 4 \\
3 & \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
2 & 4 \\
3 & 1 \\
\end{bmatrix}\\[1em]
\begin{bmatrix}
2 & 4 \\
3 & 1 \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
2 & \\
3 & 1 \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
2 & \\
3 & 1 \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
2 & 1 \\
3 & \\
\end{bmatrix} & \Rightarrow &
\begin{bmatrix}
2 & 1 \\
3 & 4 \\
\end{bmatrix}
\end{matrix}$$
列队的过程如上图所示，每一行描述了一个事件。 在第一个事件中，编号为 $1$的同学离队，这时空位在第一行第一列。接着所有同学向左标齐，这时编号为 $2$ 的同学向左移动一步，空位移动到第一行第二列。然后所有同学向上标齐，这时编号为 $4$ 的同学向上一步，这时空位移动到第二行第二列。最后编号为 $1$ 的同学返回填补到空位中。
【数据规模与约定】
| 测试点编号 | $n$ | $m$ | $q$ | 其他约定 |
| :---------: | :----------------: | :----------------: | :----------------: | :------------: |
| $1\sim 6$ | $\le 10^3$ | $\le 10^3$ | $\le 500$ | 无 |
| $7\sim 10$ | $\le 5\times 10^4$ | $\le 5\times 10^4$ | $\le 500$ | 无 |
| $11\sim 12$ | $=1$ | $\le 10^5$ | $\le 10^5$ | 所有事件 $x=1$ |
| $13\sim 14$ | $=1$ | $\le 3\times 10^5$ | $\le 3\times 10^5$ | 所有事件 $x=1$ |
| $15\sim 16$ | $\le 3\times 10^5$ | $\le 3\times 10^5$ | $\le 3\times 10^5$ | 所有事件 $x=1$ |
| $17\sim 18$ | $\le 10^5$ | $\le 10^5$ | $\le 10^5$ | 无 |
| $19\sim 20$ | $\le 3\times 10^5$ | $\le 3\times 10^5$ | $\le 3\times 10^5$ | 无 |
数据保证每一个事件满足 $1 \le x \le n,1 \le y \le m$。
### 二、解题思路
我们都知道，线段树是一种效率较高的数据结构。但是它有一个缺点，就是我们需要的空间比较大。对于权值线段树，如果我们的值域比较大，那么我们所需要的空间就是惊人的，于是我们需要采取一些策略来解决这个问题。
在线段树的应用过程中，我们可以发现，在每次修改与查询操作的时候，我们只需要针对从根节点开始最多的 $log(n)$ 个节点进行操作就可以了，那么可以发现其他的很多节点其实并没有用上，那么我们可不可以在用到某一个区间的时候动态地把他开出来而不是一次性全部开出来呢？
答案是肯定的，我们完全可以在一开始开出一个根节点代表$[1−n]$，在需要用到某个区间的时候再把这个区间所对的节点开出来供我们使用。
这样的话，可以发现我们 **舍弃** 了线段树的二倍编码原则，而是采用用 **变量记录形式来记录编号**，并且 **在递归访问的时候，把每个节点代表的区间作为参数传递**。
```cpp {.line-numbers}
struct Node{
int l,r;
int v;
}tr[N<<1];
int idx; //节点号的游标
void build(int &u){
if(u) return;
u = ++idx;
tr[u].l = tr[u].r = tr[u].v = 0;
//也可以在这里进行懒标记的初始化
return u;
}
```
动态开点线段树比较好的例题是 [$P3960$ [$NOIP2017$ 提高组] 列队](https://www.luogu.com.cn/problem/P3960)
经过观察我们可以发现，每次离队所影响的最多只是当前位置还有这一排的最后一个位置以及最后一列最后一行的位置；
于是我们可以考虑 **用一个支持单点修改的线段树**，建立$n+1$棵，前$n$棵代表第$n$行前$m−1$个答案，第$n+1$棵表示最后一列。
第一步：我们所操作的是一个长相很规整的的矩形，根据题目的操作要求，我们可以将其分为$n+1$个区间，即$n×m$的矩形分为，$n×(m−1)$的矩形和$1×n$ 的矩形，红色的矩形每一行算作一个区间，最后蓝色的一列独自成为一个区间，一共$n+1$个区间。
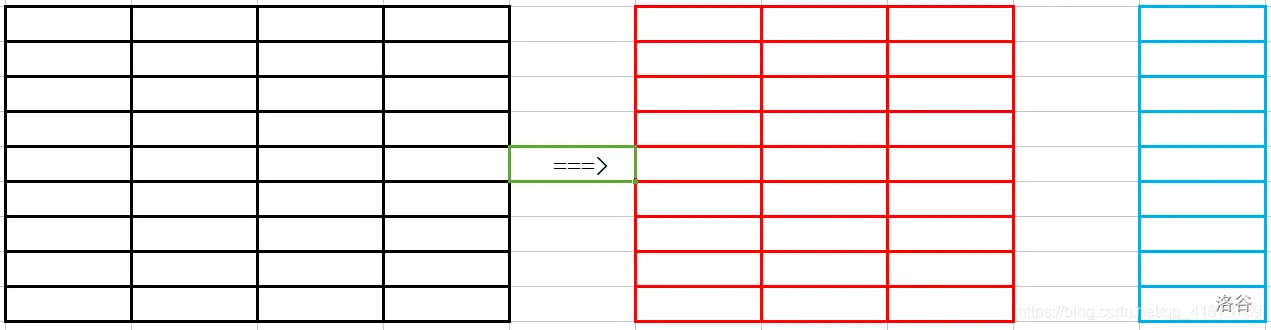
每次我们的操作就是从所有红区间中，当输入$x,y$时，即代表我们要将第$x4=$的红区间的第$y$个数取出来，$[y+1,m]$的数往前挪一位，然后蓝区间的第$x$个数就会空出，然后将蓝区间的$[x+1,n]$的数往前挪一位，蓝区间的最后一位，也就是整个矩形的右下角会空出，最后，将取出的数放入右下角这个空即可
第二步：我们因为此时的区间不是在移动就是在提取，所以是维护区间，所以自然想到了线段树，因为是维护多个区间，即多个根。所以此时要用到主席树.
第三步：一个区间约有n
个数，如果每个数都往前挪一位，q
次询问，每次询问带有n
次挪移，那么我们考虑不挪动，而是给即将空出来的位置打上标记，表示这个数已经被用过，因为区间最后会再加一个数进来，所以区间长度不变。两种方式最后留下的区间等价
```cpp {.line-numbers}
//#define LawrenceSivan
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define re register
const int maxn=3e5+5;
int n,m,q,now;
int cnt,Max;
ll ans;
struct node{
int ls,rs,size;//size:当前区间内有多少个数没有被标记
ll val;
node(){}
node(const int _ls,const int _rs,const int _size,const ll _val):
ls(_ls),rs(_rs),size(_size),val(_val){}
}st[maxn<<5];//严格来讲应该开 Q * log2(N)，也就是20倍 ，为了方便与保险，我们直接开32倍
int ins[maxn],root[maxn];
//ins[i]记录第i棵树插入了多少个新数
//root[i]记录第i棵树的根节点
inline int len(int l,int r){
if(now==n+1){
if(r<=n)return r-l+1;
if(l<=n)return n-l+1;
return 0;
}
if(r<m)return r-l+1;
if(l<m)return (m-1)-l+1;
return 0;
}
ll query(int &rt,int l,int r,int pos){
if(!rt){//动态开点
rt=++cnt;
st[rt].size=len(l,r);
if(l==r){
if(now==n+1)st[rt].val=1ll*l*m;
else st[rt].val=1ll*(now-1)*m+l;
}
}
st[rt].size--;这个区间有一个数被取出
if(l==r)return st[rt].val;
int mid=(l+r)>>1;
if(!st[rt].ls &&len(l,mid)>=pos||st[st[rt].ls].size>=pos){
query(st[rt].ls,l,mid,pos);
}
else{
int tmp;
if(!st[rt].ls)tmp=len(l,mid);
else tmp=st[st[rt].ls].size;
return query(st[rt].rs,mid+1,r,pos-tmp);
}
}
void modify(int &rt,int l,int r,int pos,ll num){
if(!rt){
rt=++cnt;
st[rt].size=len(l,r);
if(l==r){
st[rt].val=num;
}
}
++st[rt].size;//这个区间末尾有一个人进去
if(l==r)return;
int mid=(l+r)>>1;
if(pos<=mid)modify(st[rt].ls,l,mid,pos,num);
else modify(st[rt].rs,mid+1,r,pos,num);
}
inline int read() {
int x = 0, f = 1;char ch = getchar();
while (!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x * f;
}
int main() {
#ifdef LawrenceSivan
freopen("aa.in", "r", stdin);
freopen("aa.out", "w", stdout);
#endif
n=read();m=read();q=read();
Max=max(n,m)+q;//一共有q次离队，于是最多有q个人再次进队，于是最大也就是队列长度加上他们本身（因为我们取出以后在位置进行标记，相当于占上了位置
while(q--){
int x=read(),y=read();
if(y==m){//如果是最后一列
now=n+1;//那么一定要放到那个单独的区间里面去，也就是上面说到的蓝色区域
ans=query(root[now],1,Max,x);
}
else{
now=x;//否则，那么一定在红色区域
ans=query(root[now],1,Max,y);
}
printf("%lld\n",ans);//输出答案
now=n+1;//让被选出的人进入蓝色区域的最后一个位置
modify(root[now],1,Max,n+(++ins[now]),ans);
if(y!=m){
ans=query(root[now],1,Max,x);
now=x;
modify(root[now],1,Max,m-1+(++ins[now]),ans);
}
}
return 0;
}
```