python/TangDou/AcWing/SegmentTree/P3740.md

P3740 [HAOI2014] 贴海报

一、题目描述

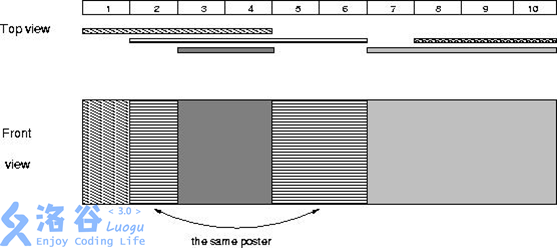
Bytetown城市要进行市长竞选，所有的选民可以畅所欲言地对竞选市长的候选人发表言论。为了统一管理，城市委员会为选民准备了一个张贴海报的electoral墙。

张贴规则如下：

1. electoral墙是一个长度为N个单位的长方形，每个单位记为一个格子；

2. 所有张贴的海报的高度必须与electoral墙的高度一致的；

3. 每张海报以“A B”表示，即从第A个格子到第B个格子张贴海报；

4. 后贴的海报可以覆盖前面已贴的海报或部分海报。

现在请你判断，张贴完所有海报后，在electoral墙上还可以看见多少张海报。

输入格式

第一行： N M 分别表示electoral墙的长度和海报个数

接下来M行: A_i B_i 表示每张海报张贴的位置

输出格式

输出贴完所有海报后，在electoral墙上还可以看见的海报数。

样例输入 #1

100 5
1 4
2 6
8 10
3 4
7 10

样例输出 #1

4

提示

【约束条件】

0<= N <= 10000000, 1<=M<=1000 , 1<= A_i <= B_i <=10000000

所有的数据都是整数。数据之间有一个空格

二、解题思路

这是一道 区间染色 类的题目。

可以用线段树来维护一个bool标记，来记录该点所辖区间是否完整被覆盖。

我们可以 从右向左遍历 全部的海报所辖区间（因为贴海报是后面的覆盖前面的），每次将这个区间放入线段树，即将线段树中的[l,r]区间内所有为false的地方改为true，但是如果该区间内的点已经全部被标记过了，那么说明这张海报不会露出来。

最后统计所有露出来的海报即为最终答案。

而由于区间范围比较大<=1e7，要 离散化 区间。

需要注意的是,由于是 区间覆盖 问题，所以普通离散化会出问题，比如: [1,6],[1,3],[5,6]离散化后会变为[1,4],[1,2],[3,4],这样一来，原来第一个区间就会被完全覆盖,其实人家的[4]是可以被看到的,没有海报可以盖住4,你离散化后就不对了，离散化失败。

这是因为，离散化操作让不相邻的点变得相邻了，这在普通问题中没有什么影响，但在 区间覆盖 问题上就变得很关键了。

所以我们要在离散化数组中, 插入r[i]+1,防止后续点不相邻的点在离散化后和它相邻 。

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int n, m;
int x[N], y[N];
bool flag; // 当前枚举到的海报是不是能被看到

// 推荐版本:静态离散化+区间覆盖
#define ls (u << 1)
#define rs (u << 1 | 1)
#define mid ((l + r) >> 1)
struct Node {
    int l, r;
    bool color; // 是不是所辖区间被完整覆盖
} tr[N << 2];

void pushup(int u) {
    tr[u].color = tr[ls].color && tr[rs].color; // 只有左儿子被完整覆盖，并且，右儿子被完整覆盖，自己才是被完整覆盖
}

void build(int u, int l, int r) {
    tr[u].l = l, tr[u].r = r;
    if (l == r) return;
    build(ls, l, mid);
    build(rs, mid + 1, r);
}

void modify(int u, int L, int R) {
    int l = tr[u].l, r = tr[u].r;
    if (l > R || r < L) return;
    if (tr[u].color) return; // 如果本区间原来就已经被覆盖过了，那么返回，也就不会在这段区间使得flag=true,也就是这个区域是看不到的
    if (l >= L && r <= R) {  // 如果以前没有被覆盖过，并且，本次本区域被完整覆盖,也就是第一次覆盖
        flag = true;         // 当前枚举到的海报可以被看到
        tr[u].color = true;  // 记录本区域被完整覆盖
        return;
    }
    modify(ls, L, R), modify(rs, L, R);
    pushup(u);
}
int b[N << 1], bl; // 离散化数组

int main() {
#ifndef ONLINE_JUDGE
    freopen("P3740.in", "r", stdin);
#endif
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        cin >> x[i] >> y[i];
        b[++bl] = x[i];
        b[++bl] = y[i];
        b[++bl] = y[i] + 1; // 区间覆盖问题的解决之道
    }
    // 排序+去重 (要注意b数组的范围，bl代表了它的上界！)
    sort(b + 1, b + 1 + bl);
    int tot = unique(b + 1, b + 1 + bl) - b - 1;

    // 构建线段树
    build(1, 1, tot);

    int res = 0;
    for (int i = m; i; i--) { // 倒序
        flag = false;         // 当前枚举到的海报是不是能被看到,默认是不能被看到
        int L = lower_bound(b + 1, b + 1 + tot, x[i]) - b;
        int R = lower_bound(b + 1, b + 1 + tot, y[i]) - b;
        modify(1, L, R); // 覆盖掉【L,R】
        if (flag) res++; // 如果当前枚举到的海报可以被看到,那么多了一张
    }
    // 输出答案
    printf("%d\n", res);
    return 0;
}

三、珂朵莉树解法

不懂珂朵莉树的同学可以看看oi wiki的介绍

简单来说珂朵莉树的原理就是维护拥有相同元素的区间

struct Node {
	int l, r;
	mutable int v;
	const bool operator<(const Node &b) const{
		return l < b.l;
	}
};

具体到本题就是将一整张海报的区间当作一个节点，每个不同的海报的区间染上不同的颜色，加入新的海报就相当于珂朵莉树的 assign 操作

最后暴力的扫一遍[1, 0] (整个墙)这个区间 记录访问到的颜色的种类(初始时整个墙围一整个区间 颜色v为0)

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;

// 用于记录颜色的集合
set<int> colors;

// 柯朵莉树模板
struct Node {
    int l, r;
    mutable int v;
    bool operator<(const Node &b) const {
        return l < b.l;
    }
};
set<Node> s;

// 分裂:[l,x-1],[x,r]
set<Node>::iterator split(int x) {
    auto it = s.lower_bound({x});
    if (it != s.end() && it->l == x) return it; // 如果x就是一个区间的开头，就不用切割,直接返回这个区间

    it--;
    if (it->r < x) return s.end(); // x太大，超过了最后一个区间的右端点,直接返回s.end()

    int l = it->l, r = it->r, v = it->v;
    s.erase(it);                      // 删掉旧区间
    s.insert({l, x - 1, v});          // 拆分成两个区间
    return s.insert({x, r, v}).first; // 返回新插入区间位置的迭代器
}

void add(int l, int r, int v) {
    auto R = split(r + 1), L = split(l);
    for (auto it = L; it != R; it++) it->v += v;
}

void assign(int l, int r, int v) {
    auto R = split(r + 1), L = split(l);
    s.erase(L, R);
    s.insert({l, r, v});
}

// 计算有多少种可见颜色
int countColor(int l, int r) {
    auto R = split(r + 1), L = split(l);
    for (auto it = L; it != R; it++)
        if (it->v) colors.insert(it->v);
    return colors.size();
}

int main() {
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);

    int n, m;
    cin >> n >> m;

    // 初始时整个区间颜色id为0
    s.insert({1, n, 0});

    // m个区间统一赋值为i
    for (int i = 1; i <= m; i++) {
        int l, r;
        cin >> l >> r;
        assign(l, r, i); // 给海报区间染色 每个区间颜色不同
    }
    // 输出有几种可见的颜色
    cout << countColor(1, n) << endl;

    return 0;
}