|
|
## [$P1204$ [$USACO1.2$] 挤牛奶$Milking$ $Cows$](https://www.luogu.com.cn/problem/P1204)
|
|
|
|
|
|
### 题目描述
|
|
|
|
|
|
三个农民每天清晨 $5$ 点起床,然后去牛棚给三头牛挤奶。
|
|
|
|
|
|
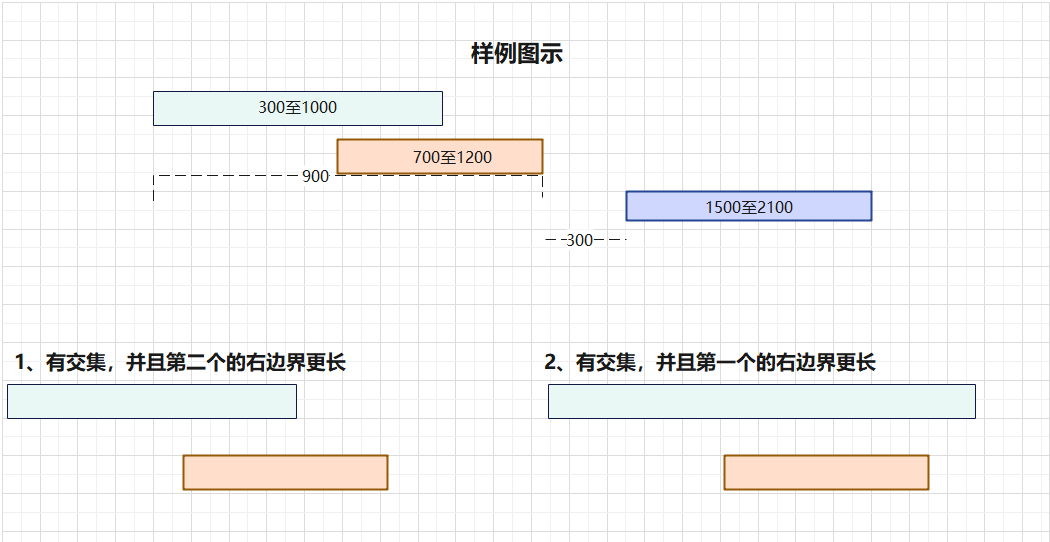
第一个农民在 $300$ 秒 (从 $5$ 点开始计时) 给他的牛挤奶,一直到 $1000$ 秒。第二个农民在 $700$ 秒开始,在 $1200$ 秒结束。第三个农民在 $1500$ 秒开始,$2100$ 秒结束。
|
|
|
|
|
|
期间最长的至少有一个农民在挤奶的连续时间为 $900$ 秒 (从 $300$ 秒到 $1200$ 秒),而最长的无人挤奶的连续时间(从挤奶开始一直到挤奶结束)为 $300$ 秒 (从 $1200$ 秒到 $1500$ 秒)。
|
|
|
|
|
|
你的任务是编一个程序,读入一个有 $n$ 个农民挤 $n$ 头牛的工作时间列表,计算以下两点(均以秒为单位):
|
|
|
|
|
|
最长至少有一人在挤奶的时间段。
|
|
|
|
|
|
最长的无人挤奶的时间段。(从有人挤奶开始算起)
|
|
|
|
|
|
### 输入格式
|
|
|
|
|
|
第一行一个正整数 $n$
|
|
|
|
|
|
接下来 $n$ 行,每行两个非负整数 $l,r$,表示一个农民的开始时刻与结束时刻。
|
|
|
|
|
|
## 输出格式
|
|
|
|
|
|
一行,两个整数,即题目所要求的两个答案。
|
|
|
|
|
|
### 样例 #1
|
|
|
|
|
|
#### 样例输入 #1
|
|
|
|
|
|
```
|
|
|
3
|
|
|
300 1000
|
|
|
700 1200
|
|
|
1500 2100
|
|
|
```
|
|
|
|
|
|
#### 样例输出 #1
|
|
|
|
|
|
```
|
|
|
900 300
|
|
|
```
|
|
|
|
|
|
### 提示
|
|
|
|
|
|
【数据范围】
|
|
|
对于 $100\%$ 的数据,$1\le n \le 5000$,$0 \le l \le r \le 10^6$。
|
|
|
|
|
|
题目翻译来自NOCOW。
|
|
|
|
|
|
USACO Training Section 1.2
|
|
|
|
|
|
|
|
|
|
|
|
### 贪心、线段重合、求最大重叠段长度和最大间距
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
const int N = 5010;
|
|
|
|
|
|
struct Node {
|
|
|
int st, ed;
|
|
|
const bool operator<(const Node &b) {
|
|
|
return st < b.st; // 按开始时间排序
|
|
|
}
|
|
|
} a[N];
|
|
|
|
|
|
// 贪心:线段重合 求最大重叠段长度和最大间距
|
|
|
int main() {
|
|
|
#ifndef ONLINE_JUDGE
|
|
|
freopen("P1204.in", "r", stdin);
|
|
|
#endif
|
|
|
int n;
|
|
|
cin >> n;
|
|
|
for (int i = 1; i <= n; i++) cin >> a[i].st >> a[i].ed;
|
|
|
sort(a + 1, a + 1 + n);
|
|
|
|
|
|
int st = a[1].st, ed = a[1].ed;
|
|
|
int mx1 = ed - st; // 最长有人的时间段
|
|
|
int mx2 = 0; // 最长无人的时间段
|
|
|
|
|
|
for (int i = 2; i <= n; i++) {
|
|
|
if (a[i].st <= ed) { // 前后连接上
|
|
|
ed = max(ed, a[i].ed); // 更新终点ed
|
|
|
mx1 = max(mx1, ed - st); // 更新一下最长的有人的时间段
|
|
|
} else { // 前后没有接上
|
|
|
mx2 = max(mx2, a[i].st - ed);
|
|
|
st = a[i].st; // 更新起点
|
|
|
ed = a[i].ed; // 更新终点
|
|
|
}
|
|
|
}
|
|
|
printf("%d %d\n", mx1, mx2);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
### 柯朵莉树
|
|
|
没什么好说的自己看看吧
|
|
|
每个农夫就$assign$一下,但要注意一下细节
|
|
|
|
|
|
应该写$assign(l,r-1,1)$,查询时应写$query(mi,mx,1/0)$
|
|
|
|
|
|
同时,因为下面的代码中有$r-1$,所以初始化时应该包含下标$0$
|
|
|
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
|
|
|
// 柯朵莉树模板
|
|
|
struct Node {
|
|
|
int l, r; // l和r表示这一段的起点和终点
|
|
|
mutable int v; // v表示这一段上所有元素相同的值是多少,注意关键字 mutable,使得set中结构体属性可修改
|
|
|
bool operator<(const Node &b) const {
|
|
|
return l < b.l; // 规定按照每段的左端点排序
|
|
|
}
|
|
|
};
|
|
|
set<Node> s; // 柯朵莉树的区间集合
|
|
|
|
|
|
// 分裂:[l,x-1],[x,r]
|
|
|
set<Node>::iterator split(int x) {
|
|
|
auto it = s.lower_bound({x});
|
|
|
if (it != s.end() && it->l == x) return it; // 一击命中
|
|
|
it--; // 没有找到就减1个继续找
|
|
|
if (it->r < x) return s.end(); // 真的没找到,返回s.end()
|
|
|
|
|
|
int l = it->l, r = it->r, v = it->v; // 没有被返回,说明找到了,记录下来,防止后面删除时被破坏
|
|
|
s.erase(it); // 删除整个区间
|
|
|
s.insert({l, x - 1, v}); //[l,x-1]拆分
|
|
|
return s.insert({x, r, v}).first; //[x,r]拆分
|
|
|
}
|
|
|
|
|
|
// 区间加
|
|
|
void add(int l, int r, int v) {
|
|
|
auto R = split(r + 1), L = split(l);
|
|
|
for (; L != R; L++) L->v += v;
|
|
|
}
|
|
|
|
|
|
// 区间赋值
|
|
|
void assign(int l, int r, int v) {
|
|
|
auto R = split(r + 1), L = split(l);
|
|
|
s.erase(L, R); // 删除旧区间
|
|
|
s.insert({l, r, v}); // 增加新区间
|
|
|
}
|
|
|
|
|
|
// 区间查询
|
|
|
int query(int l, int r, bool v) {
|
|
|
int sum = 0, res = 0;
|
|
|
auto R = split(r + 1), L = split(l);
|
|
|
for (; L != R; L++)
|
|
|
if (L->v == v)
|
|
|
sum += L->r - L->l + 1;
|
|
|
else {
|
|
|
res = max(res, sum);
|
|
|
sum = 0;
|
|
|
}
|
|
|
return res;
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
// 加快读入
|
|
|
ios::sync_with_stdio(false), cin.tie(0);
|
|
|
int n;
|
|
|
cin >> n;
|
|
|
int mi = INF, mx = -INF;
|
|
|
|
|
|
// 柯朵莉树需要进行初始化,而且,最好带0,防止RE
|
|
|
s.insert({0, 1000000, 0});
|
|
|
|
|
|
while (n--) {
|
|
|
int l, r;
|
|
|
cin >> l >> r;
|
|
|
assign(l, r - 1, 1); // 这里如果l=r=1,按这样[1,0],就会出现边界问题,所以上面最初时加入了{0,1000000}
|
|
|
mi = min(mi, l);
|
|
|
mx = max(mx, r);
|
|
|
}
|
|
|
cout << query(mi, mx, 1) << ' ' << query(mi, mx, 0);
|
|
|
return 0;
|
|
|
}
|
|
|
``` |