python/TangDou/AcWing/SegmentTree/Gorgeous/区间最值操作与区间历史最值详解.md

区间最值操作与区间历史最值详解

本文讲解了一种叫做 Segment Tree Beats 的使用线段树维护区间最值操作的方法，和维护区间历史最值的常用手段。主要参考了了吉老师 2016 年集训队论文（见文末参考资料）。

前置知识：懒标记线段树。

区间最值操作

首先假设我们有一个序列 A。区间最值操作是指，给定 l,r,k，对于所有 i\in[l,r] ，将 A_i变成 \min(A_i,k) 或 \max(A_i,k) 的一种操作。下面由一道例题引入。

HDU5306. Gorgeous Sequence

给出一个长度为 n(n\leq 10^6) 的序列 A 和 m(m\leq 10^6) 次操作，每次操作为以下三种类型之一： 1. 给出 l,r,k，对于所有 i\in[l,r]，将 A_i 变成 \min(A_i,k) 2. 给出 l,r，求序列 A 区间 [l,r]的 最大值 3. 给出 l,r，求 \displaystyle \sum_{i=l}^{r}​

在这道题中，第一种操作就是 区间最值操作。我们发现，关于区间 最大值的询问 是可以使用 带懒标记的线段树维护 的，而 区间和则不是很容易求出，因为这 不能在下传标记时快速更新答案。

考虑到区间取 \min 的操作只会对 最大值超过 k 的节点产生影响，我们可以在这方面产生思路。为了使复杂度变低，线段树的一个节点要维护三个信息：

• 区间最大值 mx
• 区间严格次大值 se
• 最大值的个数 cnt

那么，一次区间 最值操作min 作用在这个节点上时，可以被分为以下三种情况：

• k≥mx，此时该操作不会对当前节点产生影响，直接退出
• se<k<mx，此时这个节点维护的区间中所有最大值都会被修改为 k，而最大值个数不变。将区间和加上 cnt\cdot(k-mx) ，打上懒标记，然后退出即可
• k\leq se，此时无法快速更新区间信息，因此我们 需要继续递归到左右子树中，回溯时合并信息

举个例子，现在要以 k=2 对下面这棵线段树维护的区间取 \min。每个节点左侧表示区间最大值，右侧表示严格次大值。

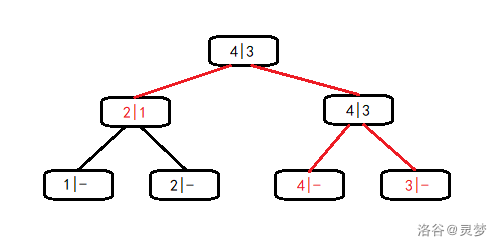
按照上面描述的操作，我们应该沿着红色的边 dfs，最后 在红色的节点上更新区间和并打上标记。

这样做的复杂度可以证明是 O(mlogn) 的。

支持区间加减

我们在支持上一道例题中所有操作的同时，加入区间加操作。

此时有两种考虑这个问题的方法：

• 套用上一题的做法，我们只需把标记换成二元组 (add,v)，表示将当前节点维护的区间先加上 add 再与 v 取最小值。合并标记 时，先考虑给当前节点加上一个标记，我们除了更新当前节点的区间加标记 add，还需要把它加到 v 上；而给当前节点取最小值可以直接将标记对它取 \min。形式地说，当节点 x 下传标记到它的儿子 ch 时，我们把儿子的标记更新为 (add_{ch}+add_x,\min(v_{ch}+add_x,v_x))即可。

• 换一种新的思路，我们发现这种方法的本质是把线段树上每个节点维护的元素分成了 最大值 和 非最大值 这两类，并对它们分别维护。区间最大值标记只会打在 se<v<mx 的节点上，可以看成只针对最大值的加减操作；而区间加操作对于这两类值都生效。分别维护 区间最大值的加减标记 和 非最大值的加减标记，下传时判断当前节点是否为区间最大值即可。

其中后者看似麻烦一些，但思想很重要，可以扩展到更复杂的问题中（尤其是后面会提到的历史最值问题），因此最好也要理解。如果还不是很明白也没有关系，在下一道例题中会详细讲解。

之前的复杂度分析在这道题无法被沿用。论文中给出了一个基于对标记的分析的 O(mlog^2n) 下界的证明，这个程序的实际运行效率是不错的。

同时支持区间最小值和最大值

BZOJ4695. 最假女选手

给出一个长度为 n(n\leq 5\times 10^5) 的序列 A 和 m(m\leq 5\times 10^5) 次操作，每次操作为以下六种类型之一：

1. 给出 l,r,k，对于所有 i\in[l,r]，将 A_i 加上 k
2. 给出 l,r,k，对于所有 i\in[l,r]，将 A_i 变成 \max(A_i,k)
3. 给出 l,r,k，对于所有 i\in[l,r]，将 A_i 变成 \min(A_i,k)
4. 给出 l,r， 求 \sum_{i=l}^{r}
5. 给出 l,r，求序列 A 区间 [l,r] 的最大值
6. 给出 l,r，求序列 A 区间 [l,r] 的最小值

在这道题中，区间取 最大值 和 最小值 的操作同时出现了。虽然我们同样可以套用第一道例题的方法，维护区间加、区间取 \max，区间取 \min 三个标记，但实现起来会很复杂（可以参考 OI-wiki 上的题解）。这里我们可以仍考虑通过划分数域 将区间最值操作转化为区间加减。

应这道题的需要，我们将一个区间的元素划分为 最大值、最小值和 其他值三种。首先在每个节点上肯定要维护区间和 sum、区间最大值 mx 和最小值 mi 的信息，同时我们也要维护次大值 semx、次小值 semi 和最大值最小值的个数 cmx,cmi。我们分别讨论题目中的三种修改操作。

• 对于加减操作，在线段树上定位区间后直接对三类值同时加上 k
• 对于取最小值操作，在线段树上暴力搜索找到 semx<k<mx 的节点。这些节点对应的区间的最大值都应该改成 k，只对最大值加上 k-mx 即可
• 取最大值操作同理

那么，我们需要分别维护这三个数域上的加减标记。但是有一些细节要注意：

• 以最大值上的加减标记为例。下传这个标记时要 判断子区间内是否包含最大值，如果 不包含则应下传其他值的加减标记

• 如果一个区间的值域很小（只有 1 或 2 个数），可能会发生一个值既是最大值又是次小值这种情况，也就是发生了数域的重叠。这种情况要特判，分辨到底该被哪个标记作用。

以上两点都会在下面的代码段中体现：

// add1, add2, add3 分别表示最小值、最大值和其他值的加减标记。
// k1, k2, k3 也是按这个顺序。
void update(int o, int k1, int k2, int k3)
// 作用标记并合并标记，一定要注意顺序
{
    if (tr[o].mn1==tr[o].mx1)// 只有一种值时，最大值等于最小值
    {
        if (k1==k3) k1=k2; else k2=k1; // 不应被其他值的标记作用
        tr[o].sum+=1ll*k1*tr[o].cmn;
    }
    else tr[o].sum+=1ll*k1*tr[o].cmn+1ll*k2*tr[o].cmx
        +1ll*k3*(tr[o].r-tr[o].l+1-tr[o].cmn-tr[o].cmx);

    if (tr[o].mn2==tr[o].mx1) tr[o].mn2+=k2;
    // 次小值等于最大值，应该被最大值标记作用
    else if (tr[o].mn2!=INF) tr[o].mn2+=k3;
    // 否则应该被其他值标记作用

    if (tr[o].mx2==tr[o].mn1) tr[o].mx2+=k1;
    else if (tr[o].mx2!=-INF) tr[o].mx2+=k3;
    // 对次大值同理

    tr[o].mn1+=k1, tr[o].mx1+=k2;
    tr[o].add1+=k1, tr[o].add2+=k2, tr[o].add3+=k3;
}

void pushdown(int o) {// 下传标记
    int mn=min(tr[lc].mn1, tr[rc].mn1);
    int mx=max(tr[lc].mx1, tr[rc].mx1);
    // 找出最大值和最小值

    update(lc, tr[lc].mn1==mn?tr[o].add1:tr[o].add3,
           tr[lc].mx1==mx?tr[o].add2:tr[o].add3, tr[o].add3);
    // 下传标记到左子树，若左子树中有最大值则下传最大值加减标记，否则下传其他值加减标记。对最小值同理
    update(rc, tr[rc].mn1==mn?tr[o].add1:tr[o].add3,
           tr[rc].mx1==mx?tr[o].add2:tr[o].add3, tr[o].add3);
    // 右子树同理

    tr[o].add1=tr[o].add2=tr[o].add3=0;
}

https://www.luogu.com.cn/paste/092htzca

P4198 楼房重建 UOJ#515. 【UR #19】前进四 BZOJ3064. Tyvj 1518 CPU监控 SP1557. GSS2 - Can you answer these queries II UOJ#164. 【清华集训2015】V UOJ#169. 【UR #11】元旦老人与数列 P6242 【模板】线段树 3