|
|
# 线段树专题
|
|
|
|
|
|
|
|
|
## 一、线段树基础
|
|
|
|
|
|
### 1. 线段树简介
|
|
|
线段树是算法竞赛中常用的用来维护区间信息的数据结构。
|
|
|
线段树可以在很小的时间复杂度内实现 **单点修改、区间修改、区间查询**(即区间求和,求区间 $max$ ,求区间 $min$ ,区间 $gcd$ 等)操作。
|
|
|
|
|
|
但是,线段树所维护的信息,需要满足 **区间加法**。
|
|
|
|
|
|
#### 区间加法
|
|
|
如果一个区间 $[l,r]$(线段树中一个点表示一个区间)满足区间加法的意思是一个区间 $[l,r]$ 的线段树维护的信息(即区间最大值,区间最小值,区间和,区间 $gcd$ 等),可以由两个区间 $[l,mid]$ 和 $[mid+1,r]$合并而来。
|
|
|
|
|
|
### 2. 线段树的基本概念
|
|
|
线段树,是一种基于分治思想的二叉搜索树。它支持的所有操作都可以 $O(logn)$ 的时间复杂度完成。
|
|
|
|
|
|
线段树的 **基本特点**:
|
|
|

|
|
|
|
|
|
* ① 线段树的每一个节点表示一个区间
|
|
|
* ② 线段树有唯一根,这个根表示的所有会被线段树统计的总区间,一般情况下,根表示的区间就是 $[1,n]$
|
|
|
* ③ 线段树的叶子节点表示的区间为 $[x,x]$ ,且长度为 $1$
|
|
|
* ④ 线段树中如果一个节点表示的区间是 $[l,r]$ ,且这个点不为叶子节点,即 $l≠r$,那么这个节点的左子树的根表示的区间就是 $[l,mid]$ 这个节点的右子树的根表示的区间就是 $[mid+1,r]$,其中 $\large mid=⌊\frac{l+r}{2}⌋$。
|
|
|
|
|
|
### 3.线段树的存储方式
|
|
|
直接采用堆存储方式,即一颗线段树的根的编号是 $1$ ,设一个不为根的节点编号 $x$ ,则这个点的父节点是 $⌊\frac{x}{2}⌋$ ,他的两个子节点的编号分别是 $2x$ 和 $2x+1$ 。为了线段树的节点不超过存储范围,一般线段树都要开 $4n$ 的空间,即区间总长度的 $4$ 倍。
|
|
|
|
|
|
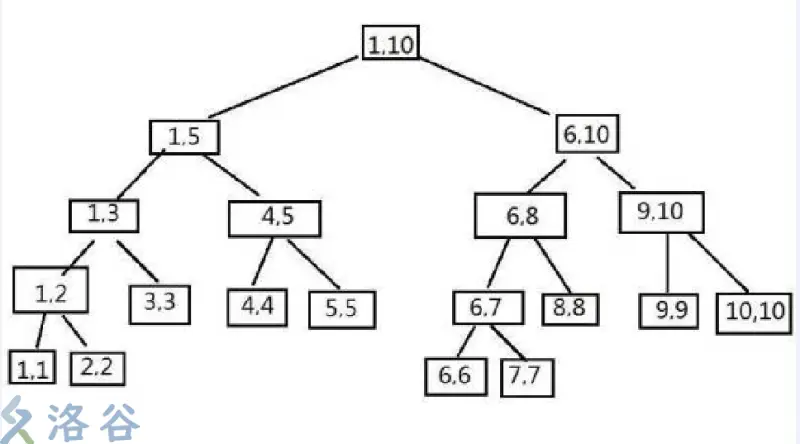
因为一颗线段树最多是一颗满二叉树,而满二叉树的最后一层是$n$ 个点,前面的点数是 $n−1$ ,所以一共要 $2n−1$ 的空间,但由于线段树有可能最后一层节点还有子节点,比如说 $n=10$ 的时候,如图:
|
|
|
<center><img src='https://cdn.acwing.com/media/article/image/2022/08/26/109870_82ea7ce424-tmp.jpg'></center>
|
|
|
|
|
|
这里就是一个例子,最后一层是多出来的,而最后一层节点最多 $2n$ 个节点,最坏情况下就最右边两个节点,最右下角的一个节点的编号是 $2n−1+2n=4n−1$ ,所以线段树一般开 $4n$ 。
|
|
|
|
|
|
### 4.建立线段树
|
|
|
**思路**
|
|
|
我们递归遍历初始区间,把遍历到的所有节点表示的区间记录下来,如果这个节点不是叶子节点(即区间长度大于$1$),那么就分别遍历左子树和右子树,否则就是叶子节点,不仅要把表示的区间记录下来,还要把线段树维护的信息也记录下来,维护的信息在叶子节点上基本上就是这个数本身。
|
|
|
时间复杂度 $O(logn)$
|
|
|
|
|
|
**代码**
|
|
|
```cpp {.line-numbers}
|
|
|
struct Node {
|
|
|
int l,r;
|
|
|
LL sum; //这里可以维护任何满足区间加法的信息,这里就用区间求和了
|
|
|
}tr[N << 2]; //要开四倍空间
|
|
|
|
|
|
void pushup (int u) { //这里只有区间和,区间和就是由一个点的左右子节点的和相加
|
|
|
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
|
|
|
}
|
|
|
|
|
|
void build (int u,int l,int r) { //当前正在下标为u的点,这个点表示的区间是[l,r]
|
|
|
if (l == r) {
|
|
|
tr[u] = {l,r,a[l]};//叶子,初始值
|
|
|
return ;
|
|
|
}
|
|
|
|
|
|
tr[u] = {l,r}; //记得存储当前点表示的区间,否则你会调上一整天
|
|
|
|
|
|
int mid = (l + r) >> 1;
|
|
|
build (u << 1,l,mid),build (u << 1 | 1,mid + 1,r); //u << 1就是u * 2,u << 1 | 1就是u * 2 + 1
|
|
|
pushup (u); //向上推送,意思是把某一个节点的信息由他的子节点算出来
|
|
|
}
|
|
|
```
|
|
|
### 5.单点修改
|
|
|
**思路**
|
|
|
我们通过二分查找的形式找到要修改的点,然后把找的过程上的链都修改一下。
|
|
|
时间复杂度 $O(logn)$
|
|
|
|
|
|
**代码**
|
|
|
```cpp {.line-numbers}
|
|
|
void change(int u,int x,int v) { //当前这个点是下标为u的点,要把第x个数修改成d
|
|
|
if (tr[u].l == tr[u].r) {
|
|
|
tr[u].sum = v; //叶子修改
|
|
|
return ;
|
|
|
}
|
|
|
int mid = tr[u].l + tr[u].r >> 1;
|
|
|
if (x <= mid) change (u << 1 , x , v); //如果在左边就递归修改左半边区间
|
|
|
else change (u << 1 | 1 , x , v); //如果在右边就递归修改右半边区间
|
|
|
pushup (u) //向上推送信息
|
|
|
}
|
|
|
```
|
|
|
|
|
|
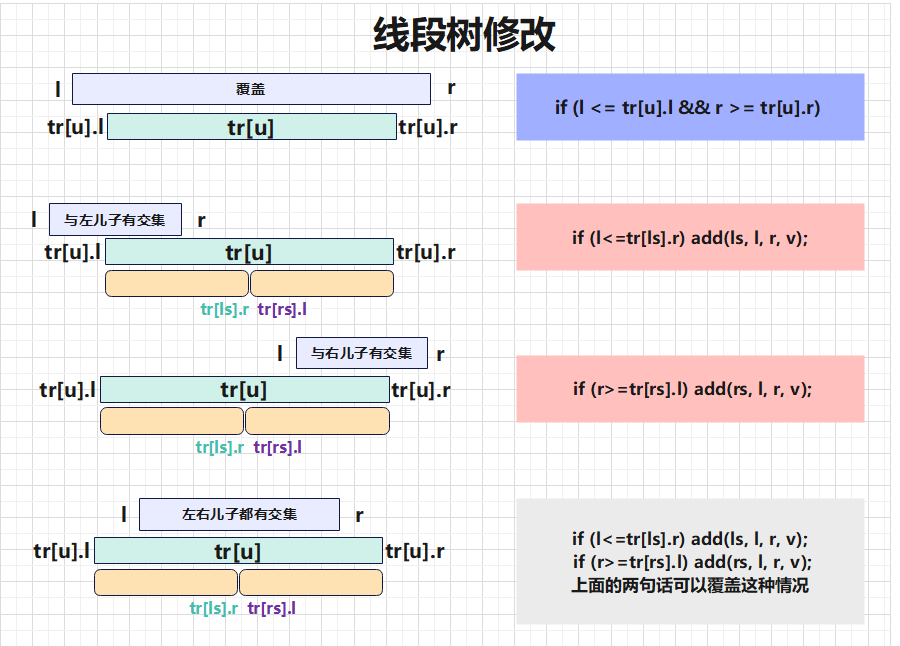
### 6.区间修改 【线段树的精髓——$Lazy$标记】
|
|
|
|
|
|
|
|
|
#### (1). $Lazy$标记是啥?有啥用?
|
|
|
> **答**:
|
|
|
>$Lazy$标记一般用在线段树的区间修改中使用了它,能将你原本需要 $O(n)$的区间修改,变得快非常多~
|
|
|
举个例子秒懂:
|
|
|
>- 省里发通知,退休人员工资普遍上涨$200$元,比即日起生效。
|
|
|
>- 市里收到通知后,领导说:不行,咱们地方财政没有钱,先计着吧,不能发,记住哪些人能多发$200$元就行了。这样多快,不用花钱,不用费事~,这叫记录懒标记,懒政嘛~
|
|
|
>- 第二个月了,领导说:把上次那些没发$200$元的所有人,都修改为$400$。这叫懒标记叠加。
|
|
|
>- 第$N$个月,省里调查组到市里调研,去$XX$厂,会询问大家工资上涨的执行情况,这时候,市领导马上让执行:把$XX$厂的欠款马上发了,别让省里调查组调查出毛病来,其它厂先记着,还是不发。这叫懒标记下放。
|
|
|
|
|
|
#### (2). 如何理解$Lazy$标记?怎么写?
|
|
|
我们再用一次之前的图
|
|
|
|
|
|
|
|
|
此时,假设初始数据为:`1 2 3 4 5 6 7 8 9 10`
|
|
|
|
|
|
我们需要将`3~7`号数据修改为`4`(当然,加上的操作也是差不多的)
|
|
|
|
|
|
正常思维我们会顺着节点编号$dfs$,找到`3~7`号数据的所有叶子节点以及路径上的父亲节点,再一一修改
|
|
|
|
|
|
慢死了对不对,最差条件下速度为 $O(n*q)$ ($q$是询问次数)
|
|
|
|
|
|
##### 现在我们使用$Lazy$标记
|
|
|
从($1,10$)节点出发,开始搜索;当搜索到($1,5$)节点时,发现$3$ ~ $7$这个数据范围未完全覆盖此区间(说人话就是,$1$~$5$区间里,$1,2$号数据是不需要修改的),然后接着搜($1,3$),($1,2$).......
|
|
|
|
|
|
恭喜你搜索到了($3,3$)节点!此时你发现$3$号数据需要修改,而($3,3$)节点是一个叶节点(叶节点的$l$与$r$相等),那么,直接修改($3,3$)节点的$max$值为$4$
|
|
|
|
|
|
接着搜,当你搜到$(4,5)$节点时,你会发现$4$号数据与$5$号数据都需要修改,如果继续搜索下去,去修改($4,4$)节点与($5,5$)节点,那就体现不出$Lazy$标记的 **懒** 之处了
|
|
|
|
|
|
我们选择不再往下搜索,而是将($4,5$)节点的$Lazy$标记修改为$4$,然后直接回溯,这样就表示($4,5$)节点覆盖的所有数据(就是$4$~$5$号数据啦)都被修改为了$4$
|
|
|
|
|
|
同理$tr[12].lazy=4$ ( 也就是($6,7$)节点的$Lazy$标记为$4$)
|
|
|
|
|
|
来看看代码
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
// 区间[l,r]统一增加v
|
|
|
void modify(int u, int l, int r, int v) {
|
|
|
if (l <= tr[u].l && r >= tr[u].r) {
|
|
|
tr[u].tag += v; // 懒标记
|
|
|
tr[u].mx += v; // 区间最大值也需要加上v
|
|
|
return;
|
|
|
}
|
|
|
// 下放懒标记
|
|
|
pushdown(u);
|
|
|
// 分裂
|
|
|
int mid = (tr[u].l + tr[u].r) >> 1;
|
|
|
if (l <= mid) modify(u << 1, l, r, v); // 与左区间有交集
|
|
|
if (r > mid) modify(u << 1 | 1, l, r, v); // 与右区间有交集
|
|
|
pushup(u); // 将结果的变更更新到祖先节点
|
|
|
}
|
|
|
```
|
|
|
第一个$if$的判断依据:若是需要修改的区间能完全覆盖当前区间,则直接修改当前区间的$Lazy$标记并回溯
|
|
|
|
|
|
#### 为什么一定要在有新的$lazy$标记修改前进入$pushdown$呢?
|
|
|
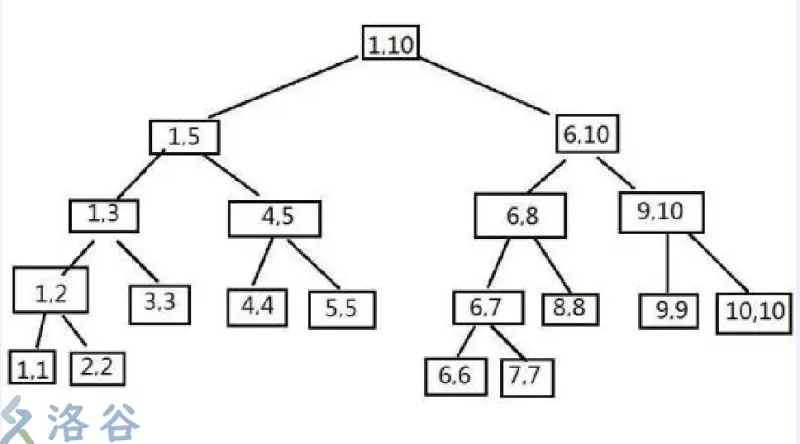
若一个区间(比如说区间($1,5$))的$Lazy$标记已经被修改为$3$,现在我们需要修改区间($1,3$)为$4$,假如我们直接修改区间($1,3$)的$Lazy$标记为$4$,那么,我们在询问$3$号数据时,会先访问到($1,5$)的$Lazy$标记,而这个$Lazy$标记会挡住$(1,3)$上的$Lazy$
|
|
|
|
|
|
> **解释**:当我们搜到($1,5$)节点时,如果它的$Lazy$标记为$3$,那么我们就默认$1$~$5$号节点都被修改为了$3$,而不会继续搜索查看下一层的子节点,这也是为什么$Lazy$标记省时间的原因。
|
|
|
|
|
|
我们再看一次之前的图(可以对着比划嗷)
|
|
|
|
|
|
|
|
|
那么我们怎么解决这个问题呢?其实很简单的一个下放操作就可以解决啦
|
|
|
|
|
|
下放操作
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
// 父节点向子节点传递懒标记
|
|
|
void pushdown(int u) {
|
|
|
auto &root = tr[u], &ls = tr[u << 1], &rs = tr[u << 1 | 1];
|
|
|
if (root.tag) { // 如果存在懒标记
|
|
|
// tag传递到子段,子段的sum和需要按 区间长度*root.tag 进行增加
|
|
|
ls.tag += root.tag, ls.sum += (LL)(ls.r - ls.l + 1) * root.tag;
|
|
|
rs.tag += root.tag, rs.sum += (LL)(rs.r - rs.l + 1) * root.tag;
|
|
|
// 清除懒标记
|
|
|
root.tag = 0;
|
|
|
}
|
|
|
}
|
|
|
|
|
|
// 以u为根,在区间[l,r]之间全都增加v
|
|
|
void modify(int u, int l, int r, int v) {
|
|
|
if (tr[u].l >= l && tr[u].r <= r) { // 如果区间完整命中
|
|
|
tr[u].sum += (LL)(tr[u].r - tr[u].l + 1) * v; // 总和增加 = 区间长度*v
|
|
|
tr[u].tag += v; // 懒标记+v
|
|
|
return;
|
|
|
}
|
|
|
|
|
|
pushdown(u); // 如果自己身上有旧的tag数值,在递归前需要将原tag值pushdown到子孙节点去
|
|
|
if (tr[ls].r >= l) modify(ls, l, r, tag);
|
|
|
if (tr[rs].l <= r) modify(rs, l, r, tag);
|
|
|
pushup(u);
|
|
|
}
|
|
|
```
|
|
|
|
|
|
代码在递归时多了一个$pushdown$操作~
|
|
|
|
|
|
仔细看这个$pushdown$,发现它其实就是把自己的$lazy$传递给了自己的两个子节点,然后将自己的$lazy$标记清零,预备下一次的修改。
|
|
|
|
|
|
我们在进行新一轮修改的时候,使用$modify$函数,一直搜索到最底层的全覆盖节点。
|
|
|
|
|
|
搜索下一层之前,如果此次修改的节点$lazy$标记为$0$,也就是它以前没有被修改过,那就不管它,继续搜索
|
|
|
|
|
|
如果$lazy$标记不为零,也就是它以前被打上过标记,那么为了避免之前说过的无法更新的情况,需要将$lazy$标记清零(以便于下次询问时不会停留在上层标记不为零的非最新标记处)
|
|
|
|
|
|
但是直接清零标记会导致区间内一部分的小区间标记丢失,于是我们采用下放操作,将父亲节点的$lazy$标记传递给两个子节点,防止信息丢失
|
|
|
|
|
|
在递归边界处,如果区间已经被完全覆盖,就不用管$lazy$标记是否会影响下层(本来就是表示的该区间内所有数据都是这个标记的意思嘛),直接修改$lazy$标记
|
|
|
|
|
|

|
|
|
|
|
|
最后,多找题写写才能理解线段树(包括各种结构,算法)的灵魂呀,去洛谷搜索 线段树 $tag$ 找题目做一做吧
|
|
|
|
|
|
### 7.区间查询
|
|
|
**思路**
|
|
|
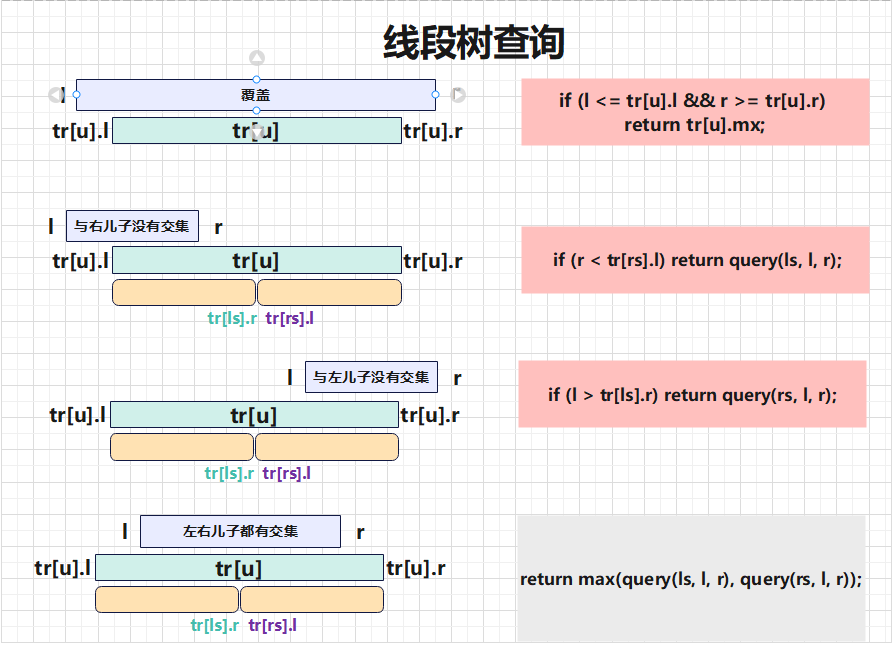
区间查询类似区间修改,只不过变为查询了。
|
|
|
|
|
|
|
|
|
|
|
|
**代码**
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
int mid = (tr[u].l + tr[u].r) >> 1;
|
|
|
int sum = 0;
|
|
|
if (l <= mid) sum += query(ls, l, r); // 左半边有被查询到的数据,就递归左半边
|
|
|
if (r >= mid + 1) sum += query(rs, l, r); // 右半边有被查询到的数据,就递归右半边
|
|
|
return sum;
|
|
|
```
|
|
|
**或者**
|
|
|
```cpp {.line-numbers}
|
|
|
if (tr[ls].r < l) return query(rs, l, r);
|
|
|
if (tr[rs].l > r) return query(ls, l, r);
|
|
|
return query(ls, l, r) + query(rs, l, r);
|
|
|
```
|
|
|
时间复杂度 $O(logn)$
|
|
|
|
|
|
|
|
|
### 二、题单
|
|
|
|
|
|
**[$AcWing$ $1275$. 最大数](https://www.cnblogs.com/littlehb/p/16152232.html)**
|
|
|
**【单点修改,区间查询】**
|
|
|
|
|
|
**[$AcWing$ $245$. 你能回答这些问题吗](https://www.cnblogs.com/littlehb/p/16152783.html)**
|
|
|
**【单点修改,区间最大子段和,前缀最大值+后缀最大值+区间和+整体最大值】**
|
|
|
|
|
|
**[$AcWing$ $246$. 区间最大公约数](https://www.cnblogs.com/littlehb/p/16152939.html)**
|
|
|
**[单点修改,区间查询,差分,更相减损数,推式子,记录$sum$和,记录最大公约数,最大公约数具有传递性]**
|
|
|
|
|
|
**[$GSS1$ - $Can$ $you$ $answer$ $these$ $queries$ $I$](https://www.cnblogs.com/littlehb/p/16204025.html)**
|
|
|
**【就是上面的$AcWing$ $245$】**
|
|
|
|
|
|
**[$GSS3$ - $Can$ $you$ $answer$ $these$ $queries$ $III$](https://www.cnblogs.com/littlehb/p/16204777.html)**
|
|
|
**【区间最大子段和+单点修改,$GSS1$的小修小改版】**
|
|
|
|
|
|
**[$GSS5$ - $Can$ $you$ $answer$ $these$ $queries$ $V$](https://www.cnblogs.com/littlehb/p/16206228.html)**
|
|
|
**【有范围限制的区间最大子段和】**
|
|
|
|
|
|
**[$POJ$ $3264$ $Balanced$ $Lineup$](https://www.cnblogs.com/littlehb/p/16185270.html)**
|
|
|
**【线段树+单点修改+区间查询最大值、最小值】**
|
|
|
|
|
|
**[$HDU$ $3333$ $Turing$ $Tree$](https://www.cnblogs.com/littlehb/p/16188952.html)**
|
|
|
**【图灵树,线段树(树状数组)+单点修改+离线操作+边构建边计算+数字去重求区间和】**
|
|
|
|
|
|
**[$POJ$ $2828$ $Buy$ $Tickets$](https://www.cnblogs.com/littlehb/p/16189410.html)**
|
|
|
**【线段树+倒序枚举+单点修改+魔改版本+怪异计数区间和】**
|
|
|
|
|
|
|
|
|
**[$AcWing$ $243$. 一个简单的整数问题2](https://www.cnblogs.com/littlehb/p/16143694.html)**
|
|
|
**【区间修改+懒标记+区间查询】**
|
|
|
|
|
|
**[$HDU$ $1698$ $Just$ $a$ $Hook$](https://www.cnblogs.com/littlehb/p/16184486.html)**
|
|
|
**【区间修改统一值+区间查询】**
|
|
|
|
|
|
**[$HDU$ $3577$ $Fast$ $Arrangement$](https://www.cnblogs.com/littlehb/p/16184914.html)**
|
|
|
|
|
|
**【线段树+区间修改+维护最大值】**
|
|
|
|
|
|
**[$Luogu$ $P2894$(区间连续一段空的长度)](https://www.cnblogs.com/littlehb/p/17019449.html)**
|
|
|
**【线段树+区间修改+懒标记+维护连续空白房间数】**
|
|
|
> ① 整体最大、左最大、右最大+组装出区间,更新父亲的统计信息
|
|
|
> ② 当父亲接到修改标识,准备$pushdown$时,除了下传懒标记外,也同步更新了左右儿子的统计信息,以保证未将懒标记下传到底时,直接获取的子树统计信息也是正确的
|
|
|
|
|
|
**[$P1253$ 扶苏的问题](https://www.cnblogs.com/littlehb/p/17663960.html)**
|
|
|
**【线段树+两个懒标记(注意标记的顺序和叠加),柯朵莉树】**
|
|
|
|
|
|
|
|
|
**[$P3740$ $[HAOI2014]$ 贴海报](https://www.cnblogs.com/littlehb/p/17656780.html)**
|
|
|
**【区间覆盖问题,离散化, 插入$r[i]+1$,倒序枚举】**
|
|
|
|
|
|
**[$P1204$ $[USACO1.2]$ 挤牛奶$Milking$ $Cows$](https://www.cnblogs.com/littlehb/p/17656983.html)**
|
|
|
**【贪心、线段重合、求最大重叠段长度和最大间距、柯朵莉树】**
|
|
|
|
|
|
**[$P4979$ 矿洞:坍塌](https://www.cnblogs.com/littlehb/p/17661421.html)**
|
|
|
**【线段树,区间数字是否一致,用的是数字$HASH$,在数字数量少的情况下是可行的,柯朵莉树需要吸氧】**
|
|
|
|
|
|
**[$P2787$ 语文$1$($chin1$)- 理理思维](https://www.cnblogs.com/littlehb/p/17662149.html)**
|
|
|
**【$26$棵线段树,利用桶来排序,懒标记$TAG=1$表示区间整体修改为$1$,$TAG=2$表示区间整体修改为$0$】**
|
|
|
|
|
|
**[$SP13015$ $Counting$ $Primes$](https://www.cnblogs.com/littlehb/p/17662387.html)**
|
|
|
**【线段树,懒标记,模板题,欧拉筛】**
|
|
|
|
|
|
**[$CF915E$ $Physical$ $Education$ $Lessons$](https://www.cnblogs.com/littlehb/p/17664882.html)**
|
|
|
**【线段树解法,柯朵莉树解法】**
|
|
|
|
|
|
**[$P4344$ [$SHOI2015$]脑洞治疗仪](https://www.cnblogs.com/littlehb/p/17671651.html)**
|
|
|
**【线段树维护区间最大连续子序列和,柯朵莉树解法】**
|
|
|
|
|
|
**[$P2253$ 好一个一中腰鼓!](https://www.cnblogs.com/littlehb/p/17679450.html)**
|
|
|
**【线段树,区间内最长不重复区间长度】**
|
|
|
|
|
|
**[$P2572$ [$SCOI2010$] 序列操作](https://www.cnblogs.com/littlehb/p/17677903.html)**
|
|
|
**【线段树,$8$个属性,$2$个懒标记的线段树,难度立即提升!柯朵莉树只能过$3$个测试点】**
|
|
|
|
|
|
**[#10115. 「一本通 4.1 例 3」校门外的树](https://www.cnblogs.com/littlehb/p/17630351.html)**
|
|
|
**【左右括号问题,树状数组,线段树,单点修改】**
|
|
|
|
|
|
**[$CF444C$ $DZY$ $Loves$ $Colors$](https://www.cnblogs.com/littlehb/p/17681314.html)**
|
|
|
**【魔改线段树,根据$same$属性决策是否懒标记下传】**
|
|
|
|
|
|
|
|
|
|
|
|
#### (3)、线段树维护区间可合并信息
|
|
|
|
|
|
[$AcWing$ $1277$. 维护序列](https://www.cnblogs.com/littlehb/p/16164815.html) [扫描线+线段树+乘法加法两个懒标记]
|
|
|
|
|
|
[$POJ$ $2777$ $Count$ $Color$](https://www.cnblogs.com/littlehb/p/16199072.html) [二进制表示选择状态+线段树计算1的个数和+懒标记更新]
|
|
|
|
|
|
|
|
|
#### (4)、线段树维护区间不可合并信息(暴力计算)
|
|
|
[$GSS4$ - $Can$ $you$ $answer$ $these$ $queries$ $IV$](https://www.cnblogs.com/littlehb/p/16202039.html) [暴力开方]
|
|
|
|
|
|
[$P4145$ 上帝造题的七分钟 $2$ / 花神游历各国](https://www.cnblogs.com/littlehb/p/16202116.html)
|
|
|
这个其实就是上面那道题,一模一样,输出有点差别而已。
|
|
|
|
|
|
[$CF438D$ $The$ $Child$ $and$ $Sequence$](https://www.cnblogs.com/littlehb/p/16202919.html)[暴力取模]
|
|
|
|
|
|
#### (5)、线段树优化建图
|
|
|
[$Legacy$ - $CF786B$](https://www.cnblogs.com/littlehb/p/16195613.html)
|
|
|
|
|
|
|
|
|
#### (6)、线段树+大小转换为$01$序列+二分
|
|
|
[$P2824$ HEOI2016 排序](https://www.cnblogs.com/littlehb/p/16206924.html)
|
|
|
|
|
|
|
|
|
#### (7)、线段树维护树上信息
|
|
|
[POJ 3321 Apple Tree](https://www.cnblogs.com/littlehb/p/16198287.html) [$dfs$序求子树节点和]
|
|
|
|
|
|
据说线段树还可以应用$bfs$序,目前还没有找到合适的练习题,挖坑待填吧~
|
|
|
|
|
|
[dfs序基础讲解(小白版)](https://blog.nowcoder.net/n/4c6c919ac4e14fb0a61274d4e5fb5e12)
|
|
|
|
|
|
|
|
|
#### (8)、线段树分裂与合并
|
|
|
[$P5494$ 【模板】线段树分裂](https://www.cnblogs.com/littlehb/p/16210449.html)
|
|
|
|
|
|
[$P4556$ [$Vani$有约会]雨天的尾巴 /【模板】线段树合并](https://www.cnblogs.com/littlehb/p/16210459.html)
|
|
|
|
|
|
|
|
|
|
|
|
---
|
|
|
|
|
|
## TODO 难度太高 或者 还没有学习到
|
|
|
#### [$CF343D$ $Water$ $Tree$](https://www.luogu.com.cn/problem/CF343D)
|
|
|
**【涉及到树链剖分】**
|
|
|
|
|
|
#### [$P4690$ [$Ynoi2016$] 镜中的昆虫](https://www.luogu.com.cn/problem/P4690)
|
|
|
**【NOI级别,黑题,先不做】**
|
|
|
|