python/TangDou/AcWing/SegmentTree/珂朵莉树专题.md

珂朵莉树

珂朵莉

珂朵莉·诺塔·瑟尼欧里斯是动画《 末日时在做什么？有没有空？可以来拯救吗？》中的女主角，五位成体妖精兵之一。最强圣剑“瑟尼欧里斯”的适合者 。

在第28号浮游岛上意外跌落而与威廉相遇，并受到他的帮助。

性别：女性 年龄：15 种族：黄金妖精 -leprechaun- 发色：苍空 瞳色：凪の海 所属：成体妖精兵（等级S） 表层信念：不去反抗无可奈何的命运 里层信念：不能阻止无可救药的感情

一、引入

CF896C Willem, Chtholly and Seniorious

-- 威廉...

-- 怎么了？

-- 瑟尼欧里斯好像出了什么问题...

-- 我会看看的...

瑟尼欧里斯是一把由特殊护符按特定顺序排列组成的剑。

已经 500 年过去了，现在剑的状态很差，所以威廉决定检查一下。

瑟尼欧里斯由n 片护符组成，威廉把它们排成一列，每个护符上有一个数字 a_i​ 。

为了保养它，威廉需要进行 m 次操作。

这里有四种操作：

• 1 l r x : 将区间 [l,r] 上的数加上 x。
• 2 l r x : 将区间 [l,r] 上的数全部变为x。
• 3 l r x : 查询区间 [l,r] 的第 x 大数。
• 4 l r x y : 查询区间 [l,r] 上的数的 x 次方之和对 y 取模的值。

本题输入较为特殊，输入格式如下：

一行四个整数，分别为 n，m，seed，vmax，前两个变量意义如题目所述，后两个变量用于生成随机数据，数据生成伪代码如下:

def rnd():
    ret = seed
    seed = (seed * 7 + 13) mod 1000000007
    return ret

for i = 1 to n:
    a[i] = (rnd() mod vmax) + 1

for i = 1 to m:
    op = (rnd() mod 4) + 1
    l = (rnd() mod n) + 1
    r = (rnd() mod n) + 1

    if (l > r): 
         swap(l, r)

    if (op == 3):
        x = (rnd() mod (r - l + 1)) + 1
    else:
        x = (rnd() mod vmax) + 1

    if (op == 4):
        y = (rnd() mod vmax) + 1

二、柯朵莉树

0x01 为什么很多题解不对，照着写会RE

因为如果要用 split 操作，截取一段区间的时候，必须要先 split(r+1) ，再 split(l) ，否则会有 RE ，具体原因我后面会细说。请大家参考其他题解或者资料的时候，也注意这一点。

0x02 什么是珂朵莉树

珂朵莉树，还有个名字叫老司机树（Old Driver Tree, ODT），是一个暴力数据结构。甚至都不一定可以将其称之为数据结构了，我们不妨认为它是一类题目的暴力做法，对于随机数据比较有效。

0x03 珂朵莉树可以解决什么问题

有一类问题，对一个序列，进行一个 区间推平操作。就是把一个范围内，比如[l,r] 范围内的数字变成同一个。可能除了推平以外，还夹杂其他操作。如果数据是随机的，就可以用珂朵莉树啦。比如这道题中的操作2 ，将 [l,r] 区间内的所有数都改成 x,这就是一个区间推平操作。

0x04 珂朵莉树的基本原理

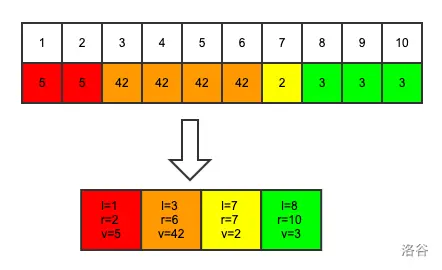
暴力的地方来喽，刚才不是提到有推平操作么？那么推平操作结束以后，被推平的区间内的每个数字都是相同的。其实经过若干次推平以后，我们可以看成，这个序列上的数字是一段一段的，每一小段里面数字相同，整个区间由若干个小段组成。类似这样：

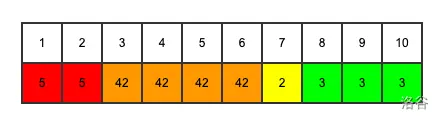
这个时候，我们定义一个结构体，用一个结构体变量，来表示每个数字相同的段。

struct Node {
    int l, r;      // l和r表示这一段的起点和终点
    mutable int v; // v表示这一段上所有元素相同的值是多少,注意关键字 mutable,使得set中结构体属性可修改
    bool operator<(const Node &b) const {
        return l < b.l; // 规定按照每段的左端点排序
    }
};

相关变量的含义，注释里面已经解释了。这里有个细节是， v 变量前面加个了 mutable 关键字。 mutable 的意思是，即使它是个常量，也允许修改v的值，具体我在下面区间修改的地方解释。

当每个数字相同的区间都用一个结构体变量表示以后，我们把这四段插入到一个 set 里面， set 会按照每段的左端点顺序进行排序，这样这个序列就维护好了，类似下图：

当然，对于本题，一开始的时候，每段都只有一个数，所以我们的set里面维护n个长度为1的段。

0x05 核心操作 split

天下大势，分久必合，合久必分，珂朵莉树也一样。随着推平操作的进行，有一些位置被合并到了一个 Node 里面，但是也有可能一个 Node 要被拆开，其中的一部分要被改变值。

split 操作就是干这个用的，参数是一个位置 x ，以 x 去做切割，找到一个包含 x 的区间，把它分成 [l,x-1] , [x,r] 两半。当然:

• ① 如果 x 本身就是一个区间的开头，就不用切割了，直接返回这个区间的迭代器
• ② 如果切割成功了，就返回两半中后面那么[x,r]区间的迭代器

先看代码

// 分裂:[l,x-1],[x,r]
set<Node>::iterator split(int x) {
    auto it = s.lower_bound({x});
    if (it != s.end() && it->l == x) return it; // x是区间开头，直接返回it迭代器
    it--;                                       // 先减1位置再说
    if (it->r < x) return s.end();              // 最后一个位置的r都小于x,返回s.end()

    int l = it->l, r = it->r, v = it->v; // 记录下来
    s.erase(it);                         // 删除整体区间
    s.insert({l, x - 1, v});             //[l,x-1]拆分    
    return s.insert({x, r, v}).first; //[x,r]拆分.insert函数返回pair，其中的first是新插入结点的迭代器
}

首先，第一行里面的 s 是一个全局变量，是那个装 Node 的 set 。大家知道 set 里面有个函数叫 lower_bound ，它的作用是返回跟参数相等的，或者比参数更大的第一个 set 中元素的位置，返回的是一个迭代器。

那么我们按照 pos 创建一个 Node ，然后去查询，就找到了 it 这个位置。这个时候有三种情况，一种是我们正好找到了一个区间，它是以 x 开头的，所以就对应了代码中的第一个 if 判断，这时候直接返回这个区间的迭代器 it。

还有两种情况是，我们找到的这个区间是正好比包含 x 的区间大一点点的，或者x太大了，超过了最后一个区间的右端点。不管怎样先把it往前挪一个格，然后这时候看看it的右端点，如果比x小，说明是x太大了，就直接返回s的end()迭代器。否则的话，现在it就是应该包含了x的那个区间。这时候，我们要把它一分为二，把原来的那个区间删掉，然后插入两个新区间，分别是[l,x-1]和[x,r]。

这里还有个小技巧，insert这个函数是有返回值的，它返回的是一个pair，pair的第一个字段正好是新插入的那个Node的位置的迭代器，所以return那个东西就行了。

0x06 推平操作assign

刚刚的split作用是分，现在还需要一个相反的操作，就是合并。当出现对区间的推平操作的时候，我们可以把整个set中所有要被合并掉的Node都删掉，然后插入一个新区间表示推平以后的结果。

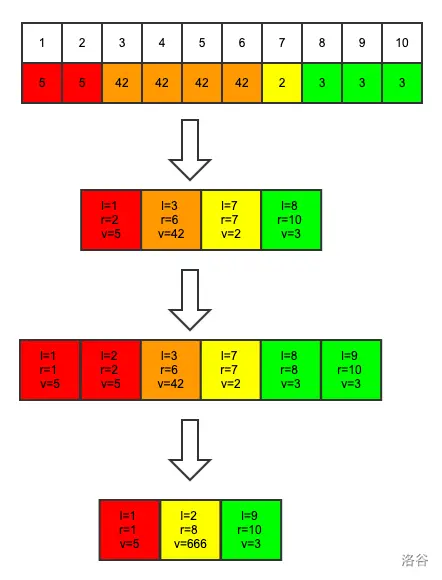
如图，按照上面的例子，set里面有4个Node，此时我们想进行一次推平操作，把[2,8]区间内的元素都改成666.首先我们发现，[8,10]是一个区间，那么需要先split(9)，把[8,8]和[9,10]拆成两个区间。同理，原来的[1,2]区间，也需要拆成[1,1]和[2,2]。

注：为啥要split(9)?因为split(x)划分开的是[l,x-1],[x,r],split(9)就会把[l,8],[9,r]割开，使得我们想操作的边界暴露出来，否则是一体化的没法整体操作。同理，split(2)就会把[1,1],[2,2]割开。

接下来，我们把要被合并的从2到8的所有Node都从set里面删掉，再重新插入一个[2,8]区间就行了。删除某个范围内的元素可以用set的erase函数，这个函数接受两个迭代器s和t，把[s,t)范围内的东西都删掉。

代码如下：

// 区间赋值
void assign(int l, int r, int x) {
    auto R = split(r + 1), L = split(l);
    s.erase(L, R);       // 删除旧区间
    s.insert({l, r, x}); // 增加新区间
}

0x07 推平操作里面RE的坑

现在说一下为啥大部分题解都不对，注意刚刚assign函数里面调用的那两次split，我是先split(r+1)，计算出itr，然后再split(l)，计算itl的。这个顺序不能反。

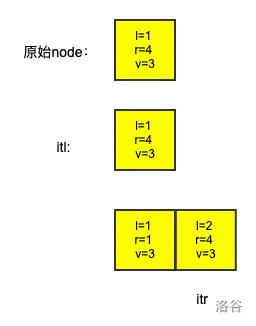
为啥不能反？举个具体例子，比如现在有个区间是[1,4]，我们想从里面截取[1,1]出来，那么我们需要调用两次split，分别是split(2)和split(1)。

假设先调用split(1)，如图中间的结果：

现在的itl指向的还是原来的那个Node，没有什么变化。但是当我们后续调用itr的时候，出事儿了。因为这时候，我们把原来的[1,4]区间删掉了，拆成了两份，itr指向的是后面那个，但是原来itl指向的那个已经被erase掉了。这时候用itl和itr调用s.erase的时候就会出问题，直接RE。

有同学说我顺序反了没RE啊，也AC。恭喜你，你人品好。这东西理论上会RE，但是实际上概率不大，我对拍了一下，大概1\%的概率RE吧。但是人品不好的同学，可能上来就RE一片，而且是随机RE，同一个数据，一会儿能过，一会儿过不了。所以，还是别给自己找麻烦了。

0x08 修改操作add

区间内每个数都加上x，这个实现方式和前面的推平差不多，我们还是找到这个区间的首尾，然后循环一遍区间内的每个Node，把每个Node的v都加上x就行

// 区间加
void add(int l, int r, int x) {
    // 必须先计算itr,后计算itl
    auto R = split(r + 1), L = split(l);
    for (auto it = L; it != R; it++) it->v += x;
}

这里是用一个迭代器it遍历每个位置，把每个位置的v都加x。大家发现前面提到的mutable的作用了么？因为这里it是个常量迭代器，它不能修改它指向的那个Node，而我们这里要改Node里面的v，所以就把v声明为mutable，就可以改了。否则会得到类似这样的编译错误： error: cannot assign to return value because function 'operator->' returns a const value

0x09 其他操作

其他操作都是类似的暴力操作。比如要找区间第k小，那么就把区间内所有的Node拿出来，按照v从小到大排序，把每个Node里面的区间长度相加，看看啥时候加够为止。这里就不细致展开，有问题可以去看代码。

// 排名第x位的数值
int rnk(int l, int r, int x) {
    vector<PII> v;
    auto R = split(r + 1), L = split(l);
    for (auto it = L; it != R; it++)
        v.push_back({it->v, it->r - it->l + 1}); // 值，个数
    sort(v.begin(), v.end());                    // 默认按PII的第一维，也就是值由小到大排序

    // 暴力拼接出排名第x大数的数值是多少
    for (auto c : v)
        if (c.second < x)
            x -= c.second;
        else
            return c.first;
}

// 快速幂 (x^y)%p
// #define int long long
int qmi(int x, int y, int p) {
    int res = 1;
    x %= p;
    while (y) {
        if (y & 1) res = res * x % p;
        y >>= 1;
        x = x * x % p;
    }
    return res;
}

int calc(int l, int r, int x, int y) {
    auto R = split(r + 1), L = split(l);
    int res = 0;
    for (auto it = L; it != R; it++)
        // it枚举的是每个区间段，每个区间段内的值是一样的：it->v
        // 区间段的长度 = it->r - it->l + 1
        // 总和 = SUM(区间段的值 * 区间段的长度)
        // 注意一步一取模
        res = (res + qmi(it->v, x, y) * (it->r - it->l + 1) % y) % y;
    return res;
}

// 用C++翻译伪代码
int rnd() {
    int ret = seed;
    seed = (seed * 7 + 13) % MOD;
    return ret;
}

0x0A 复杂度

因为本题数据是随机的，所以每次assign操作的区间长度大概在vmax/3，所以经过很多次assign以后，区间个数不会太多，大概在log这个数量级上。这样每次暴力操作的复杂度差不多也是这个数量级。详细的分析，可以参考 这篇博客

0x0B 代码时间

 珂朵莉树的核心其实就二十行左右的代码，并不是什么很难的算法，但是由于其对于数据的要求，很少有题将其作为正解，但是考场骗分还是很有用的。

#include <bits/stdc++.h>
using namespace std;
#define int long long // 太多的long long,太讨厌了，我喜欢重定义成int

const int MOD = 1000000007;
const int N = 100010;
typedef pair<int, int> PII;

int n, m;       // n 片护符,m 次操作
int seed, vmax; // 后两个变量用于生成随机数据,生成办法给了一段伪代码

// 柯朵莉树模板
struct Node {
    int l, r;      // l和r表示这一段的起点和终点
    mutable int v; // v表示这一段上所有元素相同的值是多少,注意关键字 mutable,使得set中结构体属性可修改
    bool operator<(const Node &b) const {
        return l < b.l; // 规定按照每段的左端点排序
    }
};
set<Node> s; // 柯朵莉树的区间集合

// 分裂:[l,x-1],[x,r]
set<Node>::iterator split(int x) {
    auto it = s.lower_bound({x});
    if (it != s.end() && it->l == x) return it; // 一击命中
    it--;                                       // 没有找到就减1个继续找
    if (it->r < x) return s.end();              // 真的没找到,返回s.end()

    int l = it->l, r = it->r, v = it->v; // 没有被返回，说明找到了,记录下来，防止后面删除时被破坏
    s.erase(it);                         // 删除整个区间
    s.insert({l, x - 1, v});             //[l,x-1]拆分
    // insert函数返回pair，其中的first是新插入结点的迭代器
    return s.insert({x, r, v}).first; //[x,r]拆分
}

// 区间加
void add(int l, int r, int x) {
    // 必须先计算itr,后计算itl
    auto R = split(r + 1), L = split(l);
    for (auto it = L; it != R; it++) it->v += x;
}
// 区间赋值
void assign(int l, int r, int x) {
    auto R = split(r + 1), L = split(l);
    s.erase(L, R);       // 删除旧区间
    s.insert({l, r, x}); // 增加新区间
}

// 排名第x位的数值
int rnk(int l, int r, int x) {
    vector<PII> v;
    auto R = split(r + 1), L = split(l);
    for (auto it = L; it != R; it++)
        v.push_back({it->v, it->r - it->l + 1}); // 值，个数
    sort(v.begin(), v.end());                    // 默认按PII的第一维，也就是值由小到大排序

    // 暴力拼接出排名第x大数的数值是多少
    for (auto c : v)
        if (c.second < x)
            x -= c.second;
        else
            return c.first;
}

// 快速幂 (x^y)%p
// #define int long long
int qmi(int x, int y, int p) {
    int res = 1;
    x %= p;
    while (y) {
        if (y & 1) res = res * x % p;
        y >>= 1;
        x = x * x % p;
    }
    return res;
}

//[l,r]之间，每个值的x次方，求和，对y取模
int calc(int l, int r, int x, int y) {
    auto R = split(r + 1), L = split(l);
    int res = 0;
    for (auto it = L; it != R; it++)
        // it枚举的是每个区间段，每个区间段内的值是一样的：it->v
        // 区间段的长度 = it->r - it->l + 1
        // 总和 = SUM(区间段的值 * 区间段的长度)
        // 注意一步一取模
        res = (res + qmi(it->v, x, y) * (it->r - it->l + 1) % y) % y;
    return res;
}

// 用C++翻译伪代码
int rnd() {
    int ret = seed;
    seed = (seed * 7 + 13) % MOD;
    return ret;
}

/*
参考答案：
2
1
0
3
*/
signed main() {
#ifndef ONLINE_JUDGE
    freopen("CF896C.in", "r", stdin);
#endif
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);

    cin >> n >> m >> seed >> vmax;
    for (int i = 1; i <= n; i++) {   // n 片护符
        int ai = (rnd() % vmax) + 1; // 每个护符上有一个数字 a[i]
        s.insert({i, i, ai});        // 一个格子一个数，从i~i,值为a[i]，这是在初始化构建柯朵莉树啊
    }

    for (int i = 1; i <= m; i++) { // m 个操作
        int op, l, r, x, y;
        op = (rnd() % 4) + 1;
        l = (rnd() % n) + 1;
        r = (rnd() % n) + 1;

        if (l > r) swap(l, r);

        if (op == 3)
            x = (rnd() % (r - l + 1)) + 1;
        else
            x = (rnd() % vmax) + 1;

        if (op == 4)
            y = (rnd() % vmax) + 1;
        // 上面的都是翻译伪代码

        // 真正的处理开始了
        if (op == 1)
            add(l, r, x); // 区间全部加
        else if (op == 2)
            assign(l, r, x); // 区间全部改
        else if (op == 3)
            cout << rnk(l, r, x) << endl; // 查询第x大数
        else
            cout << calc(l, r, x, y) << endl; // 查询区间 [l,r] 上的数的 x 次方之和对 y 取模的值
    }
    return 0;
}

---

Q: 为什么要Split(r + 1)？ A:便于取出 [l,r+1) 的部分，即 [l,r]

Q:为什么要先Split(r + 1)，再Split(l)？ A: 因为如果先Split(l)，返回的迭代器会位于所对应的区间以l为左端点，此时如果r 也在这个节点内，就会导致Split(l)返回的迭代器被erase掉，导致RE。

Q: 这些操作里面全是Split，复杂度理论上会退化成暴力（不断分裂直到无法再分），怎么让它不退化？

这便涉及到珂朵莉树不可或缺的操作：Assign。

Assign操作也很简单，Split之后暴力删点，然后加上一个代表当前区间的点即可。 <<<<<<< HEAD

三、习题

P3740 [HAOI2014] 贴海报

P1204 [USACO1.2] 挤牛奶Milking Cows

P4979 矿洞：坍塌

P2787 语文1（chin1）- 理理思维

SP13015 Counting Primes

CF915E Physical Education Lessons

【线段树，柯朵莉树】

P4344 [SHOI2015]脑洞治疗仪

【线段树维护区间最大连续子序列和，柯朵莉树】

P2253 好一个一中腰鼓！

【线段树，相邻不相同，最长长度】

P2572 [SCOI2010] 序列操作

【线段树,8个属性，2个懒标记的线段树，难度立即提升！柯朵莉树只能过3个测试点】

珂朵莉树（ODT）专项训练

https://www.luogu.com.cn/training/91563

P4690 [Ynoi2016] 镜中的昆虫 DZY Loves Colors #10115. 「一本通 4.1 例 3」校门外的树 校门外的树

https://www.cnblogs.com/Multitree/p/17650799.html

TODO

CF343D Water Tree（涉及到树链剖分）

=======

e52e246c9082571c684ffd7ea8565883fd93e8cf