python

8.7 KiB

Raw Permalink Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

##AcWing 906. 区间分组

一、题目描述

给定 N 个闭区间 [a_i,b_i]，请你将这些区间分成若干组，使得每组内部的区间两两之间（包括端点）没有交集，并使得 组数尽可能小。

输出最小组数。

输入格式 第一行包含整数 N，表示区间数。

接下来 N 行，每行包含两个整数 a_i,b_i，表示一个区间的两个端点。

输出格式 输出一个整数，表示最小组数。

数据范围 1≤N≤10^5,−10^9≤a_i≤b_i≤10^9

输入样例：

输出样例：

二、读懂题目

有n个区间a[i]~b[i]，将这些区间进行分组操作，要求每组内部的区间不能存在交集（有一个点共享也不行！）,求最小组数。

注意一点，只要组内所有的区间不存在交集就可以算是一个组，详情看下图:

你看，这道题很神奇吧，别看有那么多的区间，其实按照题目要求进行分组，最后分的组可能不是你想象的那样。

三、`Dilworth`定理

定理：最小不相交分组数等于最大相交组的元素个数

求 最大区间厚度 的问题,可以把这个问题想象成活动安排问题。

有若干个活动，第i个活动开始时间和结束时间是[S_i,E_i]，同一个教室安排的活动之间不能交叠，求要安排所有活动，至少需要几个教室？

有时间冲突的活动不能安排在同一间教室，与该问题的限制条件相同，最小需要的教室个数即为答案。

解法：把所有开始时间和结束时间排序，遇到开始时间就把需要的教室加1，遇到结束时间就把需要的教室减1,在一系列需要的教室个数变化的过程中，峰值就是多同时进行的活动数，也是我们至少需要的教室数。

四、实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 100100;

int b[2 * N]; // key,value:第几个端点，坐标值
int idx;      // 用于维护数组b的游标
int n;        // 共几个区间
int res = 1;  // 全放到一个组中，最小，默认值1

int main() {
    cin >> n; // n个区间
    for (int i = 1; i <= n; i++) {
        int l, r;
        cin >> l >> r;
        b[idx++] = l * 2;     // 标记左端点为偶数;同比放大2倍，还不影响排序的位置，牛~
        b[idx++] = r * 2 + 1; // 标记右端点为奇数;同比放大2倍，还不影响排序的位置，牛~
    }
    // 将所有端点放在一起排序，由小到大
    sort(b, b + idx);

    int t = 0;
    for (int i = 0; i < idx; i++) {
        if (b[i] % 2 == 0)
            t++; // 左端点+1
        else
            t--;           // 右端点-1
        res = max(res, t); // 动态计算什么时间点时，出现左的个数减去右的个数差最大，就是冲突最多的时刻
    }
    // 输出结果
    cout << res << endl;
    return 0;
}

五、可以有一个交点的情况

上面的代码是不允许存在任何两个结点开始与结束在同一个点的，比如1到3点，3到4点，算冲突。

有时这样的不算冲突，就需要另一种办法了：如果能区间端点能重合的话，端点标记的 奇数偶数反一下 就行了。因为对于同一个数,把它变成奇数比变成偶数大一,就可以咬一下啦

#include <bits/stdc++.h>

using namespace std;

const int N = 100100;

int b[2 * N]; // key,value:第几个端点，坐标值
int idx;      // 用于维护数组b的游标
int n;        // 共几个区间
int res = 1;  // 全放到一个组中，最小，默认值1

int main() {
    // n个区间
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int l, r;
        cin >> l >> r;
        b[idx++] = l * 2 + 1; // 标记左端点为奇数;同比放大2倍，还不影响排序的位置，牛~
        b[idx++] = r * 2;     // 标记右端点为偶数;同比放大2倍，还不影响排序的位置，牛~
    }
    // 将所有端点放在一起排序，由小到大
    sort(b, b + idx);

    int t = 0;
    for (int i = 0; i < idx; i++) {
        if (b[i] % 2)
            t++; // 左端点
        else
            t--;           // 右端点
        res = max(res, t); // 动态计算什么时间点时，出现左的个数减去右的个数差最大，就是冲突最多的时刻
    }
    // 输出结果
    cout << res << endl;
    return 0;
}

六、`yxc`解法

下面我们来看看该怎么做这道题目

步骤1 我们首先要做的一步是排序，让后面的操作更好梳理，这里 按左端点排序。

个人对区间选点的理解 选择左端点：需要与前面的区间进行比较选择右端点：需要与后面的区间进行比较（注：是指在思考问题，确定方案的时候，不是在写代码的时候）

步骤2 我们要做的就是枚举每个区间，看看当前区间是不是和现有的组存在交集。【或者理解为：我们看看每一个组的最后一个区间是否和当前这个区间是不是有交集。】由这种判断方式，我们可以进行如下两种操作：

如果当前枚举到的这个区间和某一个组没有交集，我们就把他放入这个组内。【即：当前区间左端点大于现在某个组的右端点，我们将这个区间归为这一组，注意更新组的右端点】
如果当前枚举到的这个区间和现有的所有的组都有交集，我们就不能将这个区间归到组内，而是要给他新开一个组。【即，当前区间的左端点小于或等于现有的所有组的右端点，我们就从新开一个组】

优化：在步骤二里面处理当前区间的时候，只有两种操作，可以说是两种选择。一个是与某一个区间没有交集（如1），一个是所有的区间都有交集（如2），但是这两种操作在具体实现的时候，都有一些小小的困难，所以，在这里我们来做一些小小的优化。我们可以这样做： 如果当前区间的左端点比最小的组的右端点都要小，这不就符合2了么，满足与所有的组都有交集的这个条件。如果不满那就属于1了，因为这个是一个二元问题，不是2就是1

这也就解释了为什么要用小根堆这个东东了，我们只要使用当前所有组的最小右端点就可以了呀！！！

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;

int n;
struct Node {
    int l, r;
    const bool operator<(const Node &b) const {
        return l < b.l; // 按照左端点进行排序
    }
} range[N];

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) cin >> range[i].l >> range[i].r;

    sort(range, range + n);

    priority_queue<int, vector<int>, greater<int>> heap; // 我们的小根堆始终保证所有组中的最小的右端点为根节点
    // 用堆来存储组的右端点

    for (int i = 0; i < n; i++) {
        auto t = range[i];

        if (heap.empty() || heap.top() >= t.l) // 如果当前队列为空，或者区间的端点小于小根堆的根（当前组的最小右端点）
            heap.push(t.r);                    // 那么这个区间就是一个大佬，和所有组都有仇，自己单开一组
        else {
            heap.pop();     // 如果大于组当中的最小右端点，说明它至少肯定和这个组没有交集，没有交集那就把它归到这一组里
            heap.push(t.r); // 既然大于我们小根堆的根，也就说明把它该归到小根堆根所代表的这一组，根就失去了作用
        }                   // 我们将根去掉，用新的t.r来放入小根堆里，小根堆替我们自动找到所有组当中为所有组的最小右端点，并作为新根
    }

    cout << heap.size() << endl; // 我们就是用size来表示的组的
    return 0;
}

七、为什么不能用右端点排序

假设有如下图所示的4个区间，按照右端点排序是1、2、3、4，进行分组得到的结果是3组。

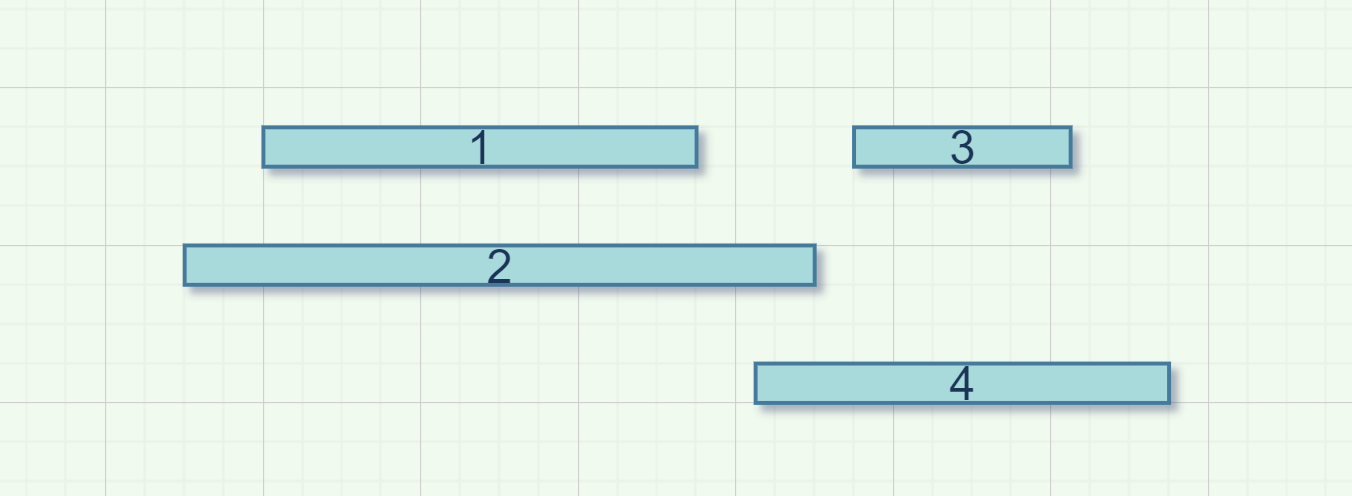
但实际上，我们可以这样分组：

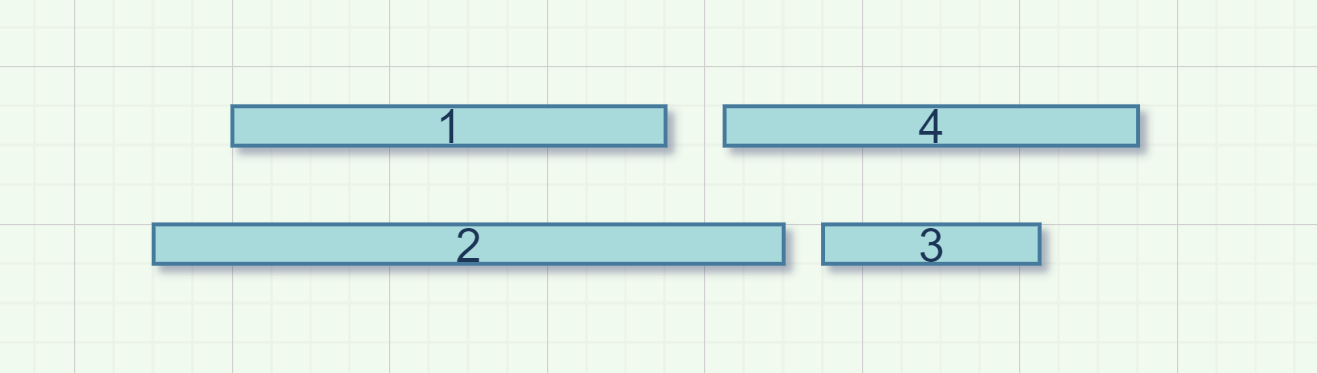
1、4一组，2、3一组，得到的正确结果是2组。

8.7 KiB Raw Permalink Blame History Unescape Escape