python/TangDou/AcWing/Section/321.md

AcWing 321 棋盘分割

一、题目描述

将一个 8×8 的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了 (n−1) 次后，连同最后剩下的矩形棋盘共有 n 块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

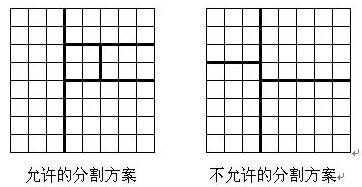
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。

现在需要把棋盘按上述规则分割成 n 块矩形棋盘，并 使各矩形棋盘总分的均方差最小。

均方差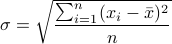 ，其中平均值 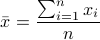，x_i 为第 i 块矩形棋盘的总分。

请编程对给出的棋盘及 n，求出 均方差的最小值。

输入格式 第 1 行为一个整数 n。

第 2 行至第 9 行每行为 8 个小于 100 的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式 输出最小均方差值（四舍五入精确到小数点后三位）。

数据范围

1<n<15

输入样例：

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

输出样例：

1.633

二、试题解析

均方差

\large δ=\sqrt{\frac{\sum\limits_{i=1}^n(x_i-\bar{x})^2}{n}}

这个东西比较讨厌，还需要开根号。因为δ>0,所以，求δ的最小值，我们可以在计算过程中一直求δ^2的最小值，到最后再统一一次开根号，效果是一样的。

平均值

\large   \bar{x}= \frac{\sum\limits_{i=1}^{n}  x_i}{n}

这个家伙比较虎人，其实仔细想想，x_i代表的含义是第i块棋盘的总分，\sum加在一起之后，就是整个棋盘的分值！这个 \bar{x}就是划分成n块棋盘后，每一块棋盘的分值平均数,也就是 整体棋盘的分值总和 /n，这是一个固定值，是常数。

转化

\large δ^2= \frac{\sum\limits_{i=1}^n(x_i-\bar{x})^2}{n}

求解

• 这个x_i是变化的，为什么会变化呢？就是因为每次切割的时候下刀的位置不同造成
• 为了切割成n块，那么需要切n-1刀
• 设计：dfs(x_1,y_1,x_2,y_2,k) 表示这个区间[x_1,y_1,x_2,y_2]在剩余k刀的情况下，可以获取到的 计算公式最大值
  • \sqrt{dfs(1,1,8,8,n-1)}
  • 递归出口：剩余刀数=0,此时，剩下的这个区域，不能继续分割，单独成块。
  • dfs分支：当拿到手一块后，发现剩余刀数大于0,应该琢磨着是按行划分，还是按列划分，还有就是划分的位置需要考虑。以按行划分为例：比如现在是[3,10]这个行区间,我们需要枚举分割线的位置，因为3可以独立成行，所以刀可以划在3上，但却不能划在10上，也就是：

  for (int i = x1; i < x2; i++) {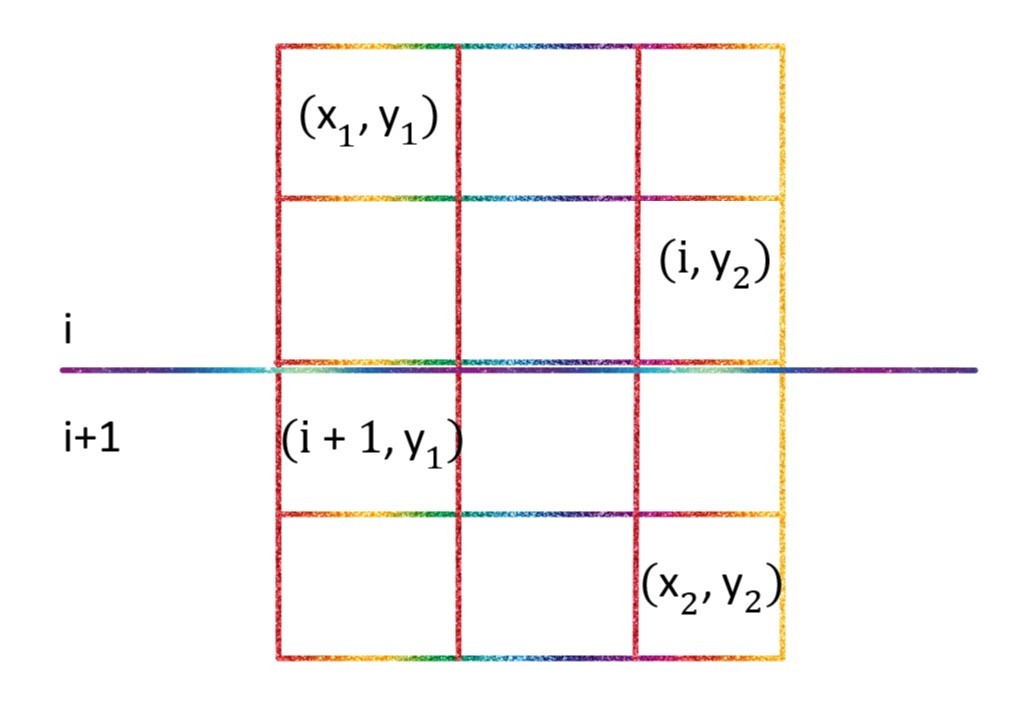
  
  }
  

  
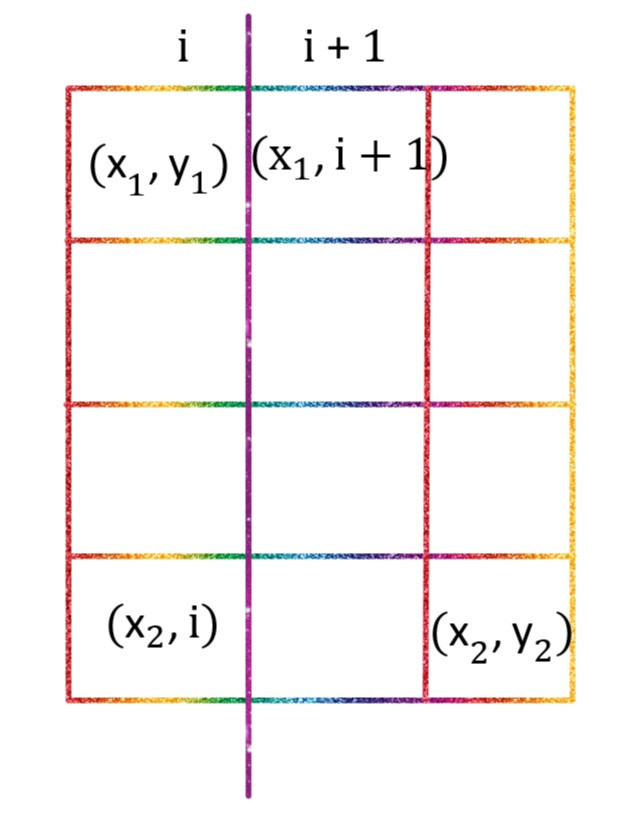
  • 刀下完之后，就得到了两个新块，这两个新块，还需经继续考虑要哪块不要哪块
  • 递归会有很多冗余的重复计算，采用 记忆化搜索 进行优化

如何枚举矩阵的分割 由于我们这里记录矩阵的状态是通过他的 对角顶点 记录的，因此分割是我们也可以通过 枚举对角 顶点 完成分割

三、记忆化搜索【推荐】

#include <bits/stdc++.h>

using namespace std;
const int N = 10; // 8*8个格子，我们从下标1开始放入，需要用到下标8，开10个。
const int INF = 0x3f3f3f3f;
int n;
int m = 8;
int s[N][N];             // 二维前缀和
double f[N][N][N][N][N]; // DP结果数组

// 二维前缀和应用
int get_sum(int x1, int y1, int x2, int y2) {
    return s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
}

// 均方差公式[模拟了题目给的公式] 注意这里没有开根号，最后开一次根号就行
double get(int x1, int y1, int x2, int y2) {
    // 利用二维前缀和的结果，计算出平均值，注意要使用double的类型转换，防止丢失精度
    double X = (double)s[m][m] / n; // 平均数
    double sum = get_sum(x1, y1, x2, y2) - X;
    return sum * sum;
}

/**
 * 功能：记忆化搜索
 * @param x1 左上角x坐标
 * @param y1 左上角y坐标
 * @param x2 右下角x坐标
 * @param y2 右下角y坐标
 * @param k  剩余的刀数
 * @return  根据公式计算出的最小值
 */
double dfs(int x1, int y1, int x2, int y2, int k) {
    double &v = f[x1][y1][x2][y2][k];
    if (v >= 0) return v;                       // 计算过了，就直接返回，不再重复计算,v是一个double,不能用~判断是不是-1
    if (k == 0) return v = get(x1, y1, x2, y2); // 如果k=0,表示刀都用完了，最终这一块可以计算出来了

    // v:-1 表示没有计算过 v:INF 马上要进行计算，先设置最大
    v = INF;

    // 每次枚举的是i和i + 1之间分界线
    // 选择横着切,从x1行开始(这个是固定的)，到i行(需要枚举的)结束
    for (int i = x1; i < x2; i++) {
        // 放弃上半部分，选择下半部分
        v = min(v, get(x1, y1, i, y2) + dfs(i + 1, y1, x2, y2, k - 1));
        // 放弃下半部分，选择上半部分
        v = min(v, get(i + 1, y1, x2, y2) + dfs(x1, y1, i, y2, k - 1));
    }
    // 选择纵着切
    for (int i = y1; i < y2; i++) {
        // 放弃左半部分，选择右半部分
        v = min(v, get(x1, y1, x2, i) + dfs(x1, i + 1, x2, y2, k - 1));
        // 放弃右半部分，选择左半部分
        v = min(v, get(x1, i + 1, x2, y2) + dfs(x1, y1, x2, i, k - 1));
    }
    // 返回打擂台的最小值
    return v;
}

int main() {
    scanf("%d", &n); // 切成n块

    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= m; j++) {
            // 原数组不用保存，直接用一个二维前缀和数组s即可
            scanf("%d", &s[i][j]);
            // 二维前缀和
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }

    // 将DP数组初始化为负无穷，计算过的>=0 (因为均方差可能为0)，未计算过的为-1,方便获取哪个位置是否计算过
    // 问题：为什么不用memset(f, -1, sizeof f)?
    // 答：一般double类型的数组初始化，喜欢用多重循环，不喜欢用memset,可能会有坑，当然，本题用memset也正确
    for (int k = 0; k < 15; k++)
        for (int x1 = 1; x1 <= m; x1++)
            for (int y1 = 1; y1 <= m; y1++)
                for (int x2 = 1; x2 <= m; x2++)
                    for (int y2 = 1; y2 <= m; y2++)
                        f[x1][y1][x2][y2][k] = -1;

    // 记忆化搜索:因为最后需要切出n块矩形棋盘，其实就是需要切n-1刀，开始dfs模拟
    printf("%.3lf\n", sqrt(dfs(1, 1, 8, 8, n - 1) / n));
    return 0;
}

四、DP 解法

与dfs就是经典的一正一反，都是OK的

#include <bits/stdc++.h>

using namespace std;
const int N = 9, M = 15;
const double INF = 0x3f3f3f3f;

double s[N][N]; // 矩阵前缀和
int n;
int m = 8;
double f[N][N][N][N][M];

double get(int x1, int y1, int x2, int y2) {
    double X = s[m][m] / n;
    double sum = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
    sum = sum - X;
    return sum * sum / n;
}

void init() {
    for (int k = 0; k < M; k++) // 注意先枚举剩余刀数
        for (int x1 = 1; x1 <= 8; x1++)
            for (int y1 = 1; y1 <= 8; y1++)
                for (int x2 = x1; x2 <= 8; x2++)
                    for (int y2 = y1; y2 <= 8; y2++)
                        if (k)
                            f[x1][y1][x2][y2][k] = INF; // 其他状态都没有到达
                        else
                            f[x1][y1][x2][y2][k] = get(x1, y1, x2, y2); // 切割0次
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= 8; i++)
        for (int j = 1; j <= 8; j++) {
            scanf("%lf", &s[i][j]);
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }

    init();

    // k的含义是剩余的刀数，为阶段概念,需要写在外层循环
    for (int k = 1; k < n; k++)
        for (int x1 = 1; x1 <= 8; x1++)
            for (int y1 = 1; y1 <= 8; y1++)
                for (int x2 = x1; x2 <= 8; x2++)
                    for (int y2 = y1; y2 <= 8; y2++) {
                        double &v = f[x1][y1][x2][y2][k];
                        // 横切
                        for (int i = x1; i < x2; i++) {
                            v = min(v, f[x1][y1][i][y2][k - 1] + get(i + 1, y1, x2, y2)); // 选上边,加下面
                            v = min(v, f[i + 1][y1][x2][y2][k - 1] + get(x1, y1, i, y2)); // 选下边
                        }

                        // 纵切
                        for (int i = y1; i < y2; i++) {
                            v = min(v, f[x1][y1][x2][i][k - 1] + get(x1, i + 1, x2, y2)); // 选左边,加右边
                            v = min(v, f[x1][i + 1][x2][y2][k - 1] + get(x1, y1, x2, i)); // 选右边
                        }
                    }

    printf("%.3f\n", sqrt(f[1][1][8][8][n - 1]));
    return 0;
}

五、总结

本题的动态规划写法，循环太多，不如采用记忆化搜索写。