python/TangDou/AcWing/Section/1068.md

AcWing ~1068. 环形石子合并

一、题目描述

将 n 堆石子绕圆形操场排放，现要将石子有序地合并成一堆。

规定每次只能选相邻的两堆合并成新的一堆，并将新的一堆的石子数记做该次合并的得分。

请编写一个程序，读入堆数 n 及每堆的石子数，并进行如下计算：

选择一种合并石子的方案，使得做 n−1 次合并得分总和最大。 选择一种合并石子的方案，使得做 n−1 次合并得分总和最小。

输入格式 第一行包含整数 n，表示共有 n 堆石子。

第二行包含 n 个整数，分别表示每堆石子的数量。

输出格式 输出共两行：

第一行为合并得分总和最小值，第二行为合并得分总和最大值。

数据范围 1≤n≤200

输入样例：

4
4 5 9 4

输出样例：

43
54

二、环形样例理解

前导知识 AcWing 282. 石子合并

三、利用区间石子合并扩展行不行

我们可不可以利用以前学习过的AcWing 282. 石子合并 那道题进行扩展来解决呢？因为共n个节点，那么就是需要合并n-1次，在图上理解就是

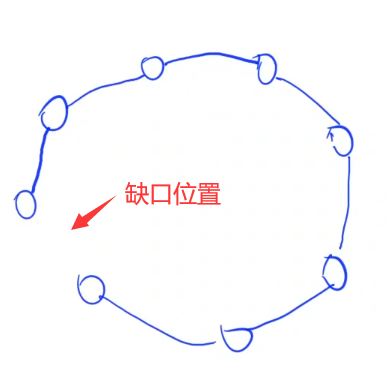
这样，我们枚举n-1次，即可以把这个环形问题转化为一个经典的区间dp问题，接下来我们计算一下时间：

原来AcWing 282. 石子合并的时间复杂度是O(N^3),这里面还需要执行n-1次，那就时间复杂度就是(n-1)\times O(N^3)=O(N^4),现在N的上限是200,200^4=1,600,000,000,会超时,此路不通。

四、环形区间问题的经典解法

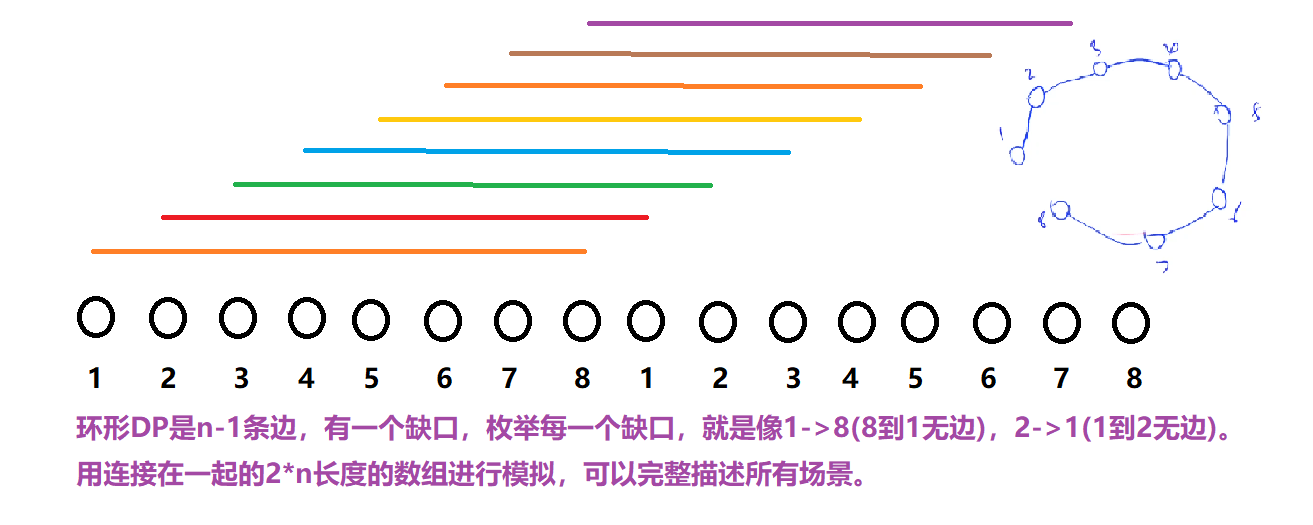
技巧：破环成链

构造一个长度为2*n的区间，模拟尾首相连。

启发我们在长度是2n的链上进行一次石子合并问题，预处理出来所有的区间f[i][j],然后枚举区间长度为n的所有子区间，就一定能枚举到n种情况了。f[i][j]->f[i][j+n-1]

这样的时间复杂度就是O((2\times N)^3),然后再通过一次常数的O(N)就可以搞定了，看清楚，这两个时间复杂度是加法关系，如此，我们就把一个时间复杂度是O(N^4)的算法，优化为一个O((2\times N)^3)级别的算法，400^3=64,000,000 是可以一秒通过的,而且这个办法是一个通用办法，是可以把环形问题转化。

五、环形区间DP

#include <bits/stdc++.h>

using namespace std;
const int N = 410; // 准备两倍的空间
const int INF = 0x3f3f3f3f;
int n;       // n个节点
int s[N];    // 前缀和
int a[N];    // 记录每个节点的石子数量
int f[N][N]; // 区间DP的数组(最大值)
int g[N][N]; // 区间DP的数组(最小值)

// 环形DP：通用办法
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]), a[i + n] = a[i]; // 复制后半段的数组,构建一个长度为2*n的数组，环形DP问题的处理技巧
    // 预处理前缀和
    for (int i = 1; i <= n * 2; i++) s[i] = s[i - 1] + a[i];

    // 预求最小，先放最大
    memset(f, 0x3f, sizeof f);

    // 预求最大，先放最小
    memset(g, -0x3f, sizeof g);

    // len=1时，代价0
    for (int i = 1; i <= 2 * n; i++) f[i][i] = g[i][i] = 0;

    // 区间DP的迭代式经典写法
    for (int len = 2; len <= n; len++)               // 枚举区间长度
        for (int l = 1; l + len - 1 <= n * 2; l++) { // 枚举左端点
            // 计算出右端点
            int r = l + len - 1;
            // 枚举分界点k
            for (int k = l; k < r; k++) {
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
                g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);
            }
        }
    // 因为从哪个位置断开环都是可行的，所以，我们依次检查一下
    int Min = INF, Max = -INF;
    for (int i = 1; i <= n; i++) {
        Min = min(Min, f[i][i + n - 1]);
        Max = max(Max, g[i][i + n - 1]);
    }
    // 输出
    printf("%d\n%d\n", Min, Max);
    return 0;
}

六、记忆化搜索代码

#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;

const int N = 410; // 注意开双倍空间
int a[N];          // 原始数组
int s[N];          // 前缀和
int f[N][N];       // 最小得分,从i堆合并到j堆的最小代价
int g[N][N];       // 最大得分,从i堆合并到j堆的最大代价
int n, m;

// 搜索出l~r的最小得分
int dfs1(int l, int r) {      // 求出最小得分
    int &v = f[l][r];         // 利用C++特性，定义一个v,简化代码
    if (l == r) return v = 0; // l==r时返回0
    if (v) return v;          // 已保存的状态不必搜索
    int res = INF;            // 初始值赋为最大值以求最小值
    // 枚举l~r之间的每个可能k,之所以k∈[l,r),可以看下面的递推关系式dfs1(k+1,r)决定了k最大是r-1
    for (int k = l; k < r; k++)
        res = min(res, dfs1(l, k) + dfs1(k + 1, r));
    return v = res + s[r] - s[l - 1]; // 记录状态
}

// 搜索出l~r的最大得分
int dfs2(int l, int r) {      // 求出最大得分
    int &v = g[l][r];         // 利用C++特性，定义一个v,简化代码
    if (l == r) return v = 0; // 若初始值为0可省略该句
    if (v) return v;          // l==r时返回0
    int res = 0;              // 初始值设为0
    for (int k = l; k < r; k++)
        res = max(res, dfs2(l, k) + dfs2(k + 1, r));
    return v = res + s[r] - s[l - 1]; // 记录状态
}

int main() {
    scanf("%d", &n);
    // 破环成链
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]), a[i + n] = a[i];
    // 前缀和
    for (int i = 1; i <= 2 * n; i++) s[i] = s[i - 1] + a[i];

    // 搜索出1-2*n的最小得分
    dfs1(1, 2 * n);

    // 搜索出1-2*n的最大得分
    dfs2(1, 2 * n);

    int ans1 = INF, ans2 = 0;
    for (int i = 1; i <= n; i++) {
        ans1 = min(f[i][n + i - 1], ans1); // 选出最小答案
        ans2 = max(g[i][n + i - 1], ans2); // 选出最大答案
    }
    printf("%d \n%d", ans1, ans2);
    return 0;
}