9.2 KiB
一、题目描述
给定 n 组 a_i,p_i,其中 p_i 是质数,求 a_i 模 p_i 的乘法逆元,若逆元不存在则输出 impossible。
注意:请返回在 0∼p−1 之间的逆元。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个数组 a_i,p_i,数据保证 p_i 是质数。
输出格式
输出共 n 行,每组数据输出一个结果,每个结果占一行。
若 a_i 模 p_i 的乘法逆元存在,则输出一个整数,表示逆元,否则输出 impossible。
数据范围
1≤n≤10^5,1≤a_i,p_i≤2∗10^9
输入样例:
3
4 3
8 5
6 3
输出样例:
1
2
impossible
二、逆元概念
| 序号 | 取模概念下的加减乘除 | 正确性 |
|---|---|---|
| 1 | (a + b)\% p = (a\%p + b\%p) \%p |
正确 |
| 2 | (a - b) \% p = (a\%p - b\%p) \%p |
正确 |
| 3 | (a * b) \% p = (a\%p * b\%p) \%p |
正确 |
| 4 | (a / b) \% p = (a\%p / b\%p) \%p |
错误 |
Q1:为什么除法错的?
证明是对的难,证伪的只要举一个反例:
(100/50)\%20 = 2 ≠ (100\%20) / (50\%20) \%20 = 0
对于一些题目,我们必须在中间过程中进行求余,否则数字太大,电脑存不下,那如果这个算式中出现除法,会损失精度,导致答案错误。
因为除法在取模运算时没有性质 ( a/b )\% c = (a\%c /b\%c) \%c,这个是不成立的,没法计算了,这时数学家提出了个 逆元 的概念:
比如 3 /5 \ mod \ 7 ,因为5在乘法模7的世界里的逆元是3,所以转化为 3 * 3 \ mod\ 7,就可转化为乘法的性质了,就方便计算了,就是答案2。
逆元可以代替除法,除以这个数就等于乘以这个数的逆元。
Q2:怎么理解逆元的含义?
想像你在一个加法的世界里,以0为世界的中心。有一天,你从世界的中心位置,进行了+3,突然,你想回到世界的中心,而你只能使用加法,所以你需要找一个数,让你加上这个数后,可以回到0这个世界的中心,这个数就是你在加法世界里3的逆元,也就是-3。
想像你在一个乘法取模7的世界里,以1为世界的中心,有一天,你从世界的中心位置,进行了*3 \ mod\ 7的操作,突然,你想回到世界的中心,而你只能使用乘法取模的,所以你需要找到一个数,让你乘上它再模7后,回到世界的中心,那么这个数就称为你在乘法模7世界的逆元。
举个栗子, 3 * 5\ mod\ 7 =1 那么3和5就在乘法mod7世界里互为逆元,就像是加法世界里的3和-3一样。
在这个乘法模7的世界里,逆元不是唯一的,比如 3 * 5\ mod\ 7 =1 而 3*12\ mod\ 7 =1。我们所说的求逆元一般是指逆元当中最小的那个。
三、费马小定理
内容:
当p为质数时 \large a^{p-1} \equiv 1 (mod\ p)
证明:略
举个栗子:
今天是周一,再过 3^{2008} 次方天,是周几呢?
解:因为一周7天,其实是在求3^{2008}\%7。
此时p=7,是质数,可以用费马小定理计算同余结果:
计算2008与p-1的关系,2008=6*334+4
所以3^{2008} \equiv 3^{4} (mod \quad 7) 就是 81\%7=4
今天是周一,再过四天就是周五了。
四、怎样求逆元?
-
当
p为质数时,可以用费马小定理+快速幂求逆元:\becausea^{p-1}≡1 (mod\quad p)\thereforea \times a^{p-2}≡1 (mod\quad p)\thereforea^{p-2}就是a的逆元。 -
当
p不是质数时,可以用扩展欧几里得算法求逆元: (学习到这里时先不用理会这个内容)a有逆元的充要条件是a与p互质,所以gcd(a, p) = 1假设a的逆元为x,那么有a * x ≡ 1 (mod\ p)等价:ax + py = 1exgcd(a, p, x, y)
五、实现代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
// 快速幂 (a^k)%p
int qmi(int a, int k, int p) {
int res = 1;
while (k) {
if (k & 1) res = res * a % p;
a = a * a % p;
k >>= 1;
}
return res;
}
signed main() {
int n;
cin >> n;
while (n--) {
int a, p;
cin >> a >> p;
if (a % p == 0)
puts("impossible"); // 不互质
else
printf("%lld\n", qmi(a, p - 2, p));
}
}
六、费马小定理练习
Q1: p=7 求2^{32}\ \%p
这个幂指数很大,我们不会傻傻的真的去计算出2^{32},而是利用费马小定理对指数进行缩减:
因为p=7是质数,所以使用费马小降幂,p-1=6
2^6\%p=1
在32里面,把所有6的倍数去掉,就是2^{32-6*5}=2^2=4
也就是说,我们可以把原来的32降为4,最终的答案是一样的结果。
Q2:一个多位数有2020位,它左边三位为123。当这个数最大时,它被29除所得的余数是_______。
在小学奥数中,经常会用到费马小定理解决余数问题。
-
先举一个简单的例子:
比如计算
18^{111}除以23的余数是多少。在这里,
a=18,p=23是素数,根据所以使用费马小定理,我们知道18^{(23-1)}除以23余1,即:18^{111} \equiv 18^{22 \times 5 +1} \equiv 18^{22 \times 5 } \times 18 \equiv 18 (mod 23)所以答案就是:
18。 -
回到这个问题: 这个
2020位数最大时即为123后面是2017个9。 我们设这个数是a, 则a= 124 \times 10^{2017}-1。 这个问题就转变为124 \times 10^{2017}-1除以29的余数是多少?
我们用同余运算和费马小定理有:124 \times 10^{2017} -1\equiv 8 \times 10^{72\times 28+1}-1这里因为124去除29,商是4,余数是8。商不会影响同余运算,舍去,保留余数8\equiv 8 \times 10^1 -1\equiv 80-1\equiv 21 (mod \ 29)答案就是:21怎么样,超简单吧?那么,如果
p不是素数时,这种问题又该怎么处理呢? 这时候欧拉定理和欧拉函数就要大显身手啦。
Q3:

解题思路
因为模数是101,比较小,而幂n是2019^{2019},很大!所以使用费马小降幂n\%(p-1),这里p就是101-1 = 100;
int n = 1, ans = 0;
for (int i = 1; i <= 2019; i++) n = n * 2019 % 100;
也就是说,在不断的循环计算n的过程中,我们利用费马小定理,找到了一个n',使得n'与原数n对于结果的贡献是一样的,但n'明显小于n,方便计算出来结果。
实现代码
#include <bits/stdc++.h>
using namespace std;
int main() {
int n = 1, ans = 0;
for (int i = 1; i <= 2019; i++) n = n * 2019 % 100; //计算出n'
// 1~11的n次方
for (int i = 1; i <= 11; i++) {
int x = 1;
for (int j = 1; j <= n; j++) x = x * i % 101; //降幂后可以正常按要求计算
//收集答案
ans += x;
}
//最终也要模一下101
printf("%d\n", ans % 101);
return 0;
}
Q5:

解题思路
项数比mod大很多,2019比10086小,所以不用费马小定理,用循环周期+快速幂做
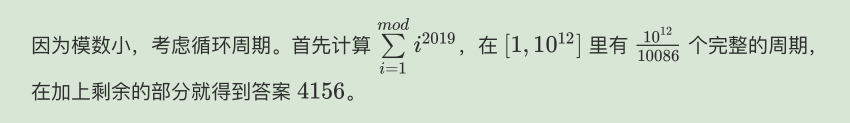
实现代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod = 10086;
LL pow_mod(LL x, LL p) {
LL res = 1;
while (p) {
if (p & 1) res = res * x % mod;
p >>= 1;
x = x * x % mod;
}
return res;
}
LL ans;
LL n = 1e12;
int main() {
for (int i = 1; i <= mod; i++) ans = (ans + pow_mod(i, 2019)) % mod; //求到10086 一个循环周期的长度
ans = ans * (n / mod) % mod; //乘上倍数
n %= mod; //再加上余数
for (int i = 1; i <= n; i++) ans = (ans + pow_mod(i, 2019)) % mod;
printf("%lld\n", ans);
return 0;
}
