python/TangDou/AcWing/NumberTriangles/1027.md

AcWing 1027. 方格取数

一、题目描述

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

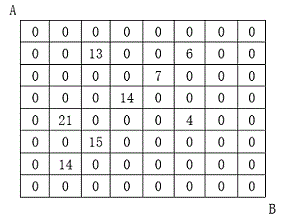
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的 数字和为最大。

输入格式 第一行为一个整数N，表示 N×N 的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

行和列编号从 1 开始。

一行0 0 0表示结束。

输出格式 输出一个整数，表示两条路径上取得的最大的和。

数据范围 N≤10

输入样例：

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

输出样例：

67

二、走两次行不行

这是一种 贪心 解法，第一次选择最大的，然后把最大路径上的数字都置为空，第二次再选择最大的。这就是 只见树木不见森林 的方法:

第一次走为局部最优并且也对第二次走造成了影响，第二次走是在第一次影响下所能走的局部最优，不具备 无后效性，因此分开两次走并不是全局最优解。

举一个反例来证明，

9 0 3
0 9 2
0 2 0

最长路径是9+9+2=20，假设这次走的路线是第一行的9、第二行的9和2，那么在第二次走的时候，地图变成

0 0 3
0 0 0
0 2 0

显然最长路径是3，总和为23。

然而,这不是最优解，最优解是第一次走第一行的9、第二行的9、第三行的2（仍是20），但第二次可以走第一行的3、第二行的2，得到5，总和达到25。

打个比方吧，以我熟悉的篮球比赛为例子，假设现在中国篮协选了杜峰和李楠两个人同时成为主教练（好奇葩的作法，是吧~），他们一起执教同一场对澳大利亚的比赛：

• 方案1：杜锋执教上半场，只关注上半场局势，不关心下半场。李楠执教下半场，只关注下半场局势，不关心上半场。结果，上半场往死了打，每个球员犯规5次，体力用尽，上半场比分与澳大利亚打平。可是到了下半场，球员都无法上场了，也没劲了，只能一节得3分，被羞辱~，为什么会这样呢？因为需要整体考虑，根据自身情况，制订合理战术，该节约体能需要节约，要控制犯规，最后一节好好冲刺，就可以与袋鼠一战，可因为两个教练互相独立，不关心另一半，当然不会考虑这些，只保证自己好就行了，最终的整体结果当然不一定是最好的。

• 方案2：两人通力合作，权衡全场，该攻就攻，该守就守，合理分配体能，不过早的暴露攻击点，最后关键时刻给敌人致命一击，成功拿下比赛，结果最重要，国家荣誉最重要。

很明显，傻子都知道方案2是最优选择。

两个小朋友 一起走 为什么就行呢？因为他们在一起整体考虑，互相关心、互相照顾~，彼此能知道对方走了哪个点，自己在不影响最优取值的情况下，尽可能的取 次优 的点，就可以得到全局最优解。

一起走:两个小朋友步调一致，“一二三” 一起走，也就是任意时刻，两人走的步数是完全一样的。

二、四维状态解法

四维的状态表示f[x_1][y_1][x_2][y_2]的含义是很明显的，就是两个小朋友分别在(x_1,y_1),(x_2,y_2)的状态下，此时的整体最优解是多少。

它的前序状态应该是

\large f(x_1,y_1,x_2,y_2) \Leftarrow  \left\{\begin{matrix}
 f(x_1-1,y_1)& f(x_2-1,y_2) & 下下 \\ 
 f(x_1-1,y_1)& f(x_2,y_2-1) & 下右 \\ 
 f(x_1,y_1-1)& f(x_2-1,y_2) & 右下\\ 
 f(x_1,y_1-1)& f(x_2,y_2-1) & 右右 
\end{matrix}\right.

这四种情况，都有可能是f[x_1][y_1][x_2][y_2]的前序，具体走哪个，可以理解为四个都试试，然后求max,谁大取谁。

int t = f[x1 - 1][y1][x2 - 1][y2];     //下下
t = max(t, f[x1][y1 - 1][x2][y2 - 1]); //右右
t = max(t, f[x1 - 1][y1][x2][y2 - 1]); //下右
t = max(t, f[x1][y1 - 1][x2 - 1][y2]); //右下

还有一个问题没有解决 : 没有加上当前状态新到的位置上的数字,讨论一下：

• ① 两个小朋友走的格子不是同一个: f[x_1][y_1][x_2][y_2]=t+w[x_1][y_1]+w[x_2][y_2]

• ② 两个小朋友走的格子是同一个 因为题目要求每个格子只能取一次，就是说如果同一时间走到同一个格子中，应该是取一次值即可: f[x_1][y_1][x_2][y_2]=t+w[x_1][y_1]

利用四层循环，从上到下，从左到右的完成状态表的填充，就可以取得正确答案：

#include <bits/stdc++.h>

using namespace std;
const int N = 15;

int n;             //方格的宽度和高度
int w[N][N];       //每个方格里面的数字
int f[N][N][N][N]; //四维的DP数组

int main() {
    cin >> n;
    //接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。
    int a, b, c;
    //一行 0 0 0 表示结束。
    while (cin >> a >> b >> c, a || b || c) w[a][b] = c;
    //开始递推
    for (int x1 = 1; x1 <= n; x1++)
        for (int y1 = 1; y1 <= n; y1++)
            for (int x2 = 1; x2 <= n; x2++)
                for (int y2 = 1; y2 <= n; y2++) {
                    if (x1 + y1 == x2 + y2) {
                        int t = f[x1 - 1][y1][x2 - 1][y2];     //下下
                        t = max(t, f[x1][y1 - 1][x2][y2 - 1]); //右右
                        t = max(t, f[x1 - 1][y1][x2][y2 - 1]); //下右
                        t = max(t, f[x1][y1 - 1][x2 - 1][y2]); //右下
                        //加上这个点的数值
                        f[x1][y1][x2][y2] = t + w[x1][y1];
                        //如果这个点没有被重复走，那么再加一次w(x2,y2)
                        if (x1 != x2 && y1 != y2) f[x1][y1][x2][y2] += w[x2][y2];
                    }
                }
    printf("%d", f[n][n][n][n]);
    return 0;
}

三、四维状态优化版本

上面四维的写法，就足以AC掉这道题了，但是在时间上还是可以优化的。原因是使用瞪眼大法仔细看，明白上面的递推关系式中，(x_1,y_1)与(x_2,y_2)其实是有关系的，刚才我们把关系写在了四层循环的内侧，这样其实有很多情况是无效的枚举，我们只关心x_1+y_1=x_2+y_2的情况，所以可以利用这个关系式，减少一层循环：

#include <bits/stdc++.h>

using namespace std;
const int N = 15;

int n;              //方格的宽度和高度
int w[N][N];        //每个方格里面的数字
int f[N][N][N][N];  //四维的DP数组

int main() {
    cin >> n;
    //接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。
    int a, b, c;
    //一行 0 0 0 表示结束。
    while (cin >> a >> b >> c, a || b || c) w[a][b] = c;

    //开始递推
    for (int x1 = 1; x1 <= n; x1++)
        for (int y1 = 1; y1 <= n; y1++)
            for (int x2 = 1; x2 <= n; x2++) {
                int y2 = x1 + y1 - x2;   //通过计算可以减少一维循环
                if (y2 >= 1 && y2 <= n) { //要小心点，别整出一个不符合实际情况的数
                    //上一个状态
                    int t = f[x1 - 1][y1][x2 - 1][y2];
                    t = max(t, f[x1][y1 - 1][x2][y2 - 1]);
                    t = max(t, f[x1 - 1][y1][x2][y2 - 1]);
                    t = max(t, f[x1][y1 - 1][x2 - 1][y2]);
                    //加上这个点的数值
                    f[x1][y1][x2][y2] = t + w[x1][y1];
                    //如果这个点没有被重复走，那么再加一次
                    if (x1 != x2 && y1 != y2) f[x1][y1][x2][y2] += w[x2][y2];
                }
            }
    printf("%d", f[n][n][n][n]);
    return 0;
}

四、三维状态版本

既然刚才想到了利用两者的 坐标关系和 来实现少写一层循环，那可不可以基于这一点深挖一下，获取更大的利益呢？答案是可以的，我们可以重新定义状态：

\large f[k][x_1][x_2]

其中k是指x_1+y_1的坐标和，当k和x_1确定时，k-x_1就是y_1; 当k和x_2确定时，k-x_2就是y_2;这样的话，就 可以在空间上减小为三维表示法！

下面来思考一下起点和终点的情况：

• 起点:(1,1)是两个小朋友的出发点，所以f[2][1][1]是起点状态值，初始值是w[1][1]
• 终点：(n,n)是两个小朋友的终点，所以f[2*n][n][n]是终点状态值,也就是答案。

#include <bits/stdc++.h>

using namespace std;
const int N = 15;

int n;
int w[N][N];
int f[N * 2][N][N];

int main() {
    cin >> n;
    //接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。
    int a, b, c;
    //一行 0 0 0 表示结束。
    while (cin >> a >> b >> c, a || b || c) w[a][b] = c;

    // k表示两个小朋友所在位置的x+y的和，最多是2*n
    for (int k = 2; k <= 2 * n; k++)
        for (int x1 = 1; x1 <= n; x1++)//第一个小朋友竖着走的距离
            for (int x2 = 1; x2 <= n; x2++) {//第二个小朋友竖着走的距离
                int y1 = k - x1, y2 = k - x2; //计算横着走的距离
                //不能出界，只走有效的位置
                if (y1 >= 1 && y1 <= n && y2 >= 1 && y2 <= n) {
                    // PK获取到最优的上一个状态
                    int t = f[k - 1][x1 - 1][x2];
                    t = max(t, f[k - 1][x1 - 1][x2 - 1]);
                    t = max(t, f[k - 1][x1][x2 - 1]);
                    t = max(t, f[k - 1][x1][x2]);
                    //将本位置的数值加上
                    f[k][x1][x2] = t + w[x1][y1];
                    //如果不是重复的位置，还可以继续加上
                    if (x1 != x2 && y1 != y2) f[k][x1][x2] += w[x2][y2];
                    }
            }
    //输出DP的结果
    printf("%d\n", f[2 * n][n][n]);
    return 0;
}

五、总结与反思

• 当你发现当前的状态表示无法描述当前所有信息时，考虑增加一维状态.一维不行就增加两维
• 普通情况下的每一个状态，思考它是从哪些可能的前序状态转移而来，注意:只考虑前一步，不要把问题想复杂了
• 在状态转移式确定下来后，再考虑入口(递推起点，初始化)和出口(结果，答案)