6.0 KiB
一、定理内容
费马小定理
如果p是一个质数,而整数a不是p的倍数
\large a^{p}\equiv a (mod \ p) \large \Leftrightarrow \large a^{p-1} \equiv 1 (mod \ p)1.1 这玩意有啥用?
题目:一个多位数有2020位,它左边三位为123。当这个数最大时,它被29除所得的余数是_______。
在小学奥数中,经常会用到费马小定理解决余数问题。
-
先举一个简单的例子:
比如计算
18^{111}除以23的余数是多少。在这里,
a=18,p=23是素数,根据所以使用费马小定理,我们知道18^{(23-1)}除以23余1,即:18^{111} \equiv 18^{22 \times 5 +1} \equiv 18^{22 \times 5 } \times 18 \equiv 18 (mod 23)所以答案就是:
18。 -
回到这个问题: 这个
2020位数最大时即为123后面是2017个9。 我们设这个数是a, 则a= 124 \times 10^{2017}-1。 这个问题就转变为124 \times 10^{2017}-1除以29的余数是多少? 我们用同余运算和费马小定理有:124 \times 10^{2017} -1\equiv 8 \times 10^{72\times 28+1}-1这里因为124去除29,商是4,余数是8。商不会影响同余运算,舍去,保留余数8\equiv 8 \times 10^1 -1\equiv 80-1\equiv 21 (mod \ 29)答案就是:21怎么样,超简单吧?那么,如果
p不是素数时,这种问题又该怎么处理呢? 这时候欧拉定理和欧拉函数就要大显身手啦。
1.2 可以用来降幂
a^n \ \% p = a^{n \ \% (p-1)} \ \% p
求a的n次方,可以先n \ \% (p-1)
解释一下:
费马小定理降幂例子:
p=7
求2^{32}\ \%p
这个幂指数很大,我们不会傻傻的真的去计算出2^{32},而是利用费马小定理对指数进行缩减:
因为p=7是质数,所以使用费马小降幂,p-1=6
2^6\%p=1
在32里面,把所有6的倍数去掉,就是2^{32-6*5}=2^2=4
也就是说,我们可以把原来的32降为4,最终的答案是一样的结果。
写成通用的格式就是:
求(a^N)mod(p)
a^{p-1} \equiv 1(mod \ p)
k=N \% (p-1)
(a^N)mod(p)=(a^k)mod(p)
二、例题I
求2^{100}\%13的余数。
2的100次方,明显幂次挺大,而且13是质数,可以用费马小定理来降幂。
\large 2^{100} \equiv 2^{12*8+4} \equiv 16 \equiv 3 (mod \%13)#include <bits/stdc++.h>
using namespace std;
//计算2^100 %13的值
int fun1(int a, int p, int mod) {
//前提p是质数,a不是p的倍数,有费马小定理
int ans = pow(a, p % (mod - 1)); //利用费马小定理,降幂 p'= p % (mod - 1),然后再计算 pow(a,p'),这个就小多了
ans %= mod; //再最后模一下mod就可以了
return ans;
}
// fun2和fun3都会受到时间或者空间的限制,而fun1直接使用了费马小定理可以迅速的求取答案
int fun2(int a, int p, int mod) {
int ans = pow(a, p); //不管p多大,我就是个算~暴力!但问题是你不怕爆掉int上界?不会溢出?
ans %= mod; //最后取模
return ans;
}
int fun3(int a, int p, int mod) {
int ans = 1;
while (p--) { //既然怕爆int上界,那么就一步一取模,一步一计算。笨的要死,你不怕慢死啊:人家费马小定理只需要一步,你需要p步!而且,p还不小,慢的要死!
ans *= a;
ans %= mod;
}
ans %= mod;
return ans;
}
int main() {
for (int i = 1; i <= 100; i++) {
cout << fun1(2, i, 13) << endl;
cout << fun2(2, i, 13) << endl;
cout << fun3(2, i, 13) << endl;
}
return 0;
}
二、例题II

解题思路
因为模数是101,比较小,而幂n是2019^{2019},很大!所以使用费马小降幂n\%(p-1),这里p就是101-1 = 100;
int n = 1, ans = 0;
for (int i = 1; i <= 2019; i++) n = n * 2019 % 100;
也就是说,在不断的循环计算n的过程中,我们利用费马小定理,找到了一个n',使得n'与原数n对于结果的贡献是一样的,但n'明显小于n,方便计算出来结果。
实现代码
#include <bits/stdc++.h>
using namespace std;
int main() {
int n = 1, ans = 0;
for (int i = 1; i <= 2019; i++) n = n * 2019 % 100; //计算出n'
// 1~11的n次方
for (int i = 1; i <= 11; i++) {
int x = 1;
for (int j = 1; j <= n; j++) x = x * i % 101; //降幂后可以正常按要求计算
//收集答案
ans += x;
}
//最终也要模一下101
printf("%d\n", ans % 101);
return 0;
}
三、例题III

解题思路
项数比mod大很多,2019比10086小,所以不用费马小定理,用循环周期+快速幂做
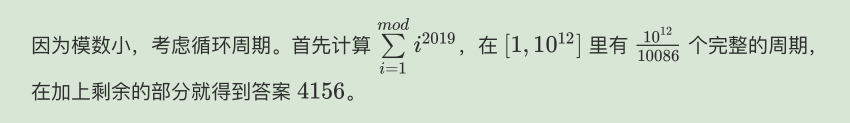
实现代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod = 10086;
LL pow_mod(LL x, LL p) {
LL res = 1;
while (p) {
if (p & 1) res = res * x % mod;
p >>= 1;
x = x * x % mod;
}
return res;
}
LL ans;
LL n = 1e12;
int main() {
for (int i = 1; i <= mod; i++) ans = (ans + pow_mod(i, 2019)) % mod; //求到10086 一个循环周期的长度
ans = ans * (n / mod) % mod; //乘上倍数
n %= mod; //再加上余数
for (int i = 1; i <= n; i++) ans = (ans + pow_mod(i, 2019)) % mod;
printf("%lld\n", ans);
return 0;
}