python/TangDou/AcWing/MultiSourceBfs/173.md

AcWing 173. 矩阵距离

一、题目描述

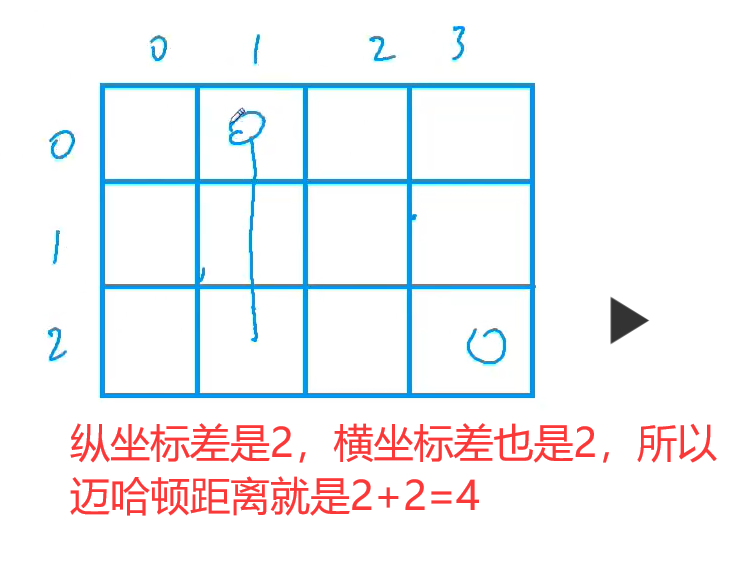
给定一个 N 行 M 列的 01 矩阵 A，A[i][j] 与 A[k][l] 之间的 曼哈顿距离 定义为：

\large dist(A[i][j],A[k][l])=|i−k|+|j−l|

输出一个 N 行 M 列的整数矩阵 B，其中：

\large B[i][j]=min_{1≤x≤N,1≤y≤M,A[x][y]=1}dist(A[i][j],A[x][y])

输入格式 第一行两个整数 N,M。

接下来一个 N 行 M 列的 01 矩阵，数字之间没有空格。

输出格式 一个 N 行 M 列的矩阵 B，相邻两个整数之间用一个空格隔开。

数据范围 1≤N,M≤1000

输入样例：

3 4
0001
0011
0110

输出样例：

3 2 1 0
2 1 0 0
1 0 0 1

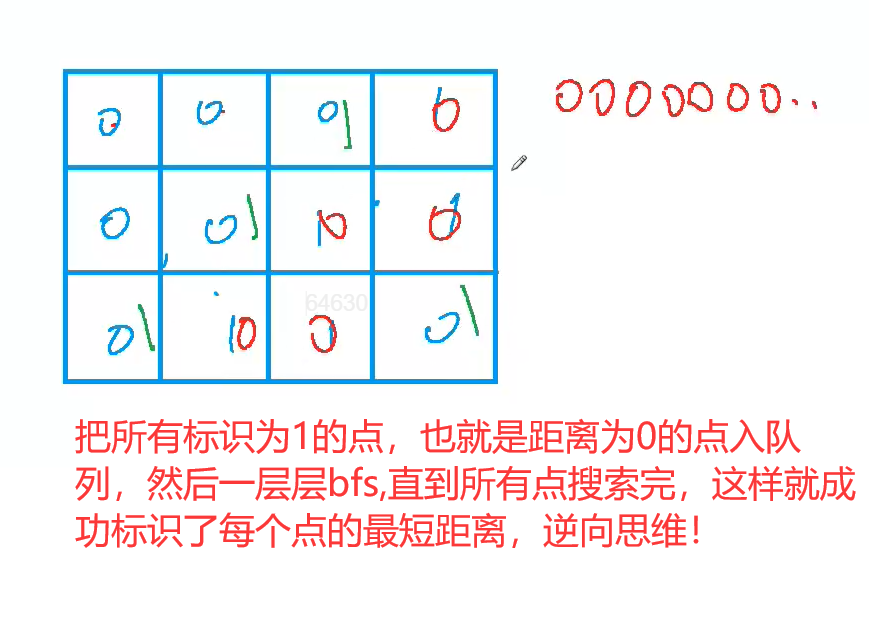
二、题意理解

三、实现代码

#include <bits/stdc++.h>

using namespace std;

#define x first
#define y second
typedef pair<int, int> PII;
const int N = 1010, M = N * N;

int n, m;
char g[N][N];
PII q[M];
int dist[N][N];

int dx[] = {-1, 0, 1, 0}; // 上右下左
int dy[] = {0, 1, 0, -1}; // 上右下左

void bfs() {
    memset(dist, -1, sizeof dist);
    int hh = 0, tt = -1;
    // 将所有位置是1的位置，也就是哈密尔顿距离为0的入队列
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            if (g[i][j] == '1') {
                dist[i][j] = 0;   // 标识距离为0，一是为了显示最终的结果，二来也有防止走回头路的作用
                q[++tt] = {i, j}; // 入队列
            }

    while (hh <= tt) {
        PII t = q[hh++];
        for (int i = 0; i < 4; i++) {
            int x = t.x + dx[i], y = t.y + dy[i];
            if (x < 1 || x > n || y < 1 || y > m) continue;
            if (~dist[x][y]) continue;
            dist[x][y] = dist[t.x][t.y] + 1;
            q[++tt] = {x, y};
        }
    }
}

int main() {
    cin >> n >> m;

    // 放过0行和0列,这个+1用的妙，一行行读入，每一行从下标1的列号开始
    // 原理就是读入到 g[i]这一行数据的地址中，并且需要偏移一个位置的地址,联想一下 scanf("%d",&a);的含义进行记忆理解
    for (int i = 1; i <= n; i++) cin >> g[i] + 1;
    // 宽搜
    bfs();

    // 输出结果矩阵
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++)
            printf("%d ", dist[i][j]);
        puts("");
    }
    return 0;
}