|
|
## [$AcWing$ $135$. 最大子序和 ](https://www.acwing.com/problem/content/137/)
|
|
|
|
|
|
### 一、题目描述
|
|
|
输入一个长度为 $n$ 的整数序列,从中找出一段 **长度不超过 $m$ 的连续子序列**,使得子序列中所有数的和最大。
|
|
|
|
|
|
注意: 子序列的长度至少是 $1$。
|
|
|
|
|
|
**输入格式**
|
|
|
第一行输入两个整数 $n,m$。
|
|
|
|
|
|
第二行输入 $n$ 个数,代表长度为 $n$ 的整数序列。
|
|
|
|
|
|
同一行数之间用空格隔开。
|
|
|
|
|
|
**输出格式**
|
|
|
输出一个整数,代表该序列的最大子序和。
|
|
|
|
|
|
**数据范围**
|
|
|
$1≤n,m≤300000$,保证所有输入和最终结果都在 `int` 范围内。
|
|
|
|
|
|
**输入样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
6 4
|
|
|
1 -3 5 1 -2 3
|
|
|
```
|
|
|
|
|
|
**输出样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
7
|
|
|
```
|
|
|
|
|
|
|
|
|
### 二、暴力作法
|
|
|
|
|
|
如果只要 **固定长度为$m$的连续子区间** 元素总和最大,那就是个简单的滑动窗口,我们先计算一下前缀和,然后维护一个滑动窗口,一边加来一边减就行了。
|
|
|
|
|
|
此题就难度提升了,因为是一个 <font color='red' size=5><b>长度不超过$m$</b></font> 的连续子区间!
|
|
|
|
|
|
窗口长度不固定,那我们就考虑枚举每个位置做为终点,然后从终点向回走,最长枚举$m$个长度,这样纯暴力的思路就出来了!
|
|
|
|
|
|
#### 暴力大法
|
|
|
$TL$E掉$3$个点
|
|
|
通过了 $11/14$个数据
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
// Brute-force 暴力
|
|
|
const int N = 300010;
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
int s[N];
|
|
|
int n, m;
|
|
|
|
|
|
// TLE掉3个点,通过了 11/14个数据
|
|
|
int main() {
|
|
|
cin >> n >> m;
|
|
|
for (int i = 1; i <= n; i++) cin >> s[i], s[i] += s[i - 1];
|
|
|
|
|
|
int res = -INF;
|
|
|
// 遍历每一个终点
|
|
|
for (int i = 1; i <= n; i++)
|
|
|
// 从终点向前,找出所有区间在m之内的数字,通过前缀和计算出区间的累加和,保留最大值
|
|
|
// 在刚刚出发不久,长度不够m的时候,即i<m,则i-m会出现负数
|
|
|
for (int j = i; j > max(0, i - m); j--)
|
|
|
res = max(res, s[i] - s[j - 1]); // j>0 && j> i-m --> j> max(0,i-m)
|
|
|
|
|
|
printf("%d\n", res);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
### 三、优化办法
|
|
|
|
|
|
本题的数据范围是$30w$,上面**平方级别复杂度**的代码显然会超时。
|
|
|
|
|
|
|
|
|
**状态表示**
|
|
|
|
|
|
$f[i]$:以第$i$个数字结尾的长度不超过$m$的子序列的最大和
|
|
|
|
|
|
$s[i]$:数组的前缀和,则$a[l] + ... + a[r] = s[r] - s[l-1]$
|
|
|
|
|
|
状态转移方程为$f[i] = max(s[i] - s[j-1])$,其中$i - j$大于等于$0$并且不超过$m$
|
|
|
|
|
|
**举个栗子**:
|
|
|
|
|
|
|
|
|
|
|
|
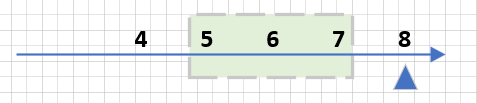
- 假设:现在$i=8,m=3$,就是要找出包括$i=8$在内,$3$个数字的窗口中,窗口的最大值:
|
|
|
$$\large res=max(a[8]+a[7]+a[6],a[8]+a[7],a[8])$$
|
|
|
|
|
|
- 每次计算累加和不好计算,我们采用前缀和优化一下
|
|
|
$$\large res=max( s[8]-s[5],s[8]-s[6],s[8]-s[7])$$
|
|
|
|
|
|
- 当前枚举到了$8$,可以认为$s[8]$是固定值,那么其实就是在求
|
|
|
$$\large min(s[5],s[6],s[7])$$
|
|
|
这些数字的特点是:$8$的左侧三个范围内,前缀和最小。典型的 **单调队列求极小值问题**。
|
|
|
|
|
|
- 推广到通用形态,当前枚举到的是$i$,那么就是在求$$\large min(s[i-1],s[i-2],…,s[i-m])$$ (可以类比一下上面的例子)
|
|
|
|
|
|
- 由上面的分析得知,其实这个窗口就是在$i$前面的$m$个位置内!不包括$i$
|
|
|
|
|
|
- 采用单调队列优化一下,可以在$O(1)$时间内找出前面$m$个数的最小值:维护一个队列,保存距离当前结点前面$i-1 \sim i-m$范围内的前缀和最小的那个结点索引下标。每次计算到$i$时,直接取队列中的队头进行计算即可。
|
|
|
因为$i$不在窗口中,当枚举到$i$时,**需要在它未加入到队列前查询队列头**!
|
|
|
|
|
|
- 考虑一下边界问题,如果$i=1$,那么它也需要向队列中去找出它前面的最小前缀和,而它是第一个进来的,还没有来得及维护队列,这样的话就找不到了,需要手动向队列中初始化一个合理的初始化值 **【哨兵】**。从本题来说,就是第一个数字前面的所有前缀和,当然是$0$,即$q[hh]=q[0]=0,tt++$; 并且因为$q$是定义在全局变量区,默认就是$0$,不用再写这句,所以直接$tt=0$就描述了初始化的过程。
|
|
|
|
|
|
|
|
|
#### 算法细节
|
|
|
在单调队列的实现时,需要先在队列中加入哨兵结点$s[0]$,后面就是解决四个问题:
|
|
|
|
|
|
* ① 何时出队头,枚举到第$i$个数字时,第$i$个数字还没加入队列时,队头元素的下标允许的最小值是$i - m$,所以当$i - q[hh] > m$时就需要出队头了
|
|
|
|
|
|
* ② 何时出队尾,我们需要队头的元素是$s[q[hh]]$最小的元素,所以当$s[i] <= s[q[tt]]$时,出队尾元素
|
|
|
|
|
|
* ③ 何时加入新元素,队尾元素该出的出完了就可以将$i$加入到队列中了
|
|
|
|
|
|
* ④ 何时更新我们要求的长度不超过$m$的子序列的和的最大值$res$,只要在确保队列中的元素个数不超过$m$时就可以尝试更新$res$了
|
|
|
|
|
|
#### 时间复杂度
|
|
|
使用单调队列优化$DP$的方法时间复杂度是$O(n)$。
|
|
|
|
|
|
|
|
|
### 四、单调队列实现
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
const int N = 300010;
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
int n, m;
|
|
|
int q[N];
|
|
|
// 单调队列,本质记录的是下标序号,因为只有记录了下标,才能知道是否离i的距离长度超过m了没有。
|
|
|
// 同时,记录了下标的话,想要其它的信息都是可以表示出来的,比如s[q[hh]]
|
|
|
|
|
|
int s[N]; // 前缀和
|
|
|
int res = -INF; // 预求最大,先设最小
|
|
|
|
|
|
int main() {
|
|
|
cin >> n >> m;
|
|
|
for (int i = 1; i <= n; i++) cin >> s[i], s[i] += s[i - 1]; // 前缀和
|
|
|
|
|
|
int hh = 0, tt = 0; // 等价于增加了一个哨兵节点,也就是把下标为0的前缀和s[0]=0加入了滑动窗口中,描述1号节点向前m个节点的前缀和最小值是0
|
|
|
|
|
|
// 枚举右边界
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
// 1、老掉牙的需要去世
|
|
|
while (hh <= tt && q[hh] < i - m) hh++;
|
|
|
// 2、此时单调队列中保存就是i以前、长度最长为m的单调上升的一个序列,队列头保存的就是i前面前缀和的最小值
|
|
|
// 此时i还没有进入队列,单调队列其实在枚举数字i的左侧
|
|
|
res = max(res, s[i] - s[q[hh]]);
|
|
|
/*
|
|
|
把0,也就是sum(0)塞入队列中(这是给sum(1)用的,因为可能sum(1)-sum(0)就是最大的子序列,不加这个0就没法计算了),最小值为0
|
|
|
*/
|
|
|
// 3、i入队列
|
|
|
// 比i老没它小的都去死吧~
|
|
|
while (hh <= tt && s[q[tt]] >= s[i]) tt--;
|
|
|
// i入队列,本轮结束
|
|
|
q[++tt] = i;
|
|
|
}
|
|
|
// 输出结果
|
|
|
cout << res << endl;
|
|
|
return 0;
|
|
|
}
|
|
|
``` |