python/TangDou/AcWing/MonotonicQueue/1091.md

AcWing 1091. 理想的正方形

一维滑动窗口模板题 AcWing 154. 滑动窗口

一、题目描述

有一个 a×b 的整数组成的矩阵，现请你从中找出一个 n×n 的正方形区域，使得该区域所有数中的 最大值 和 最小值 的 差最小。

输入格式 第一行为三个整数，分别表示 a,b,n 的值；

第二行至第 a+1 行每行为 b 个非负整数，表示矩阵中相应位置上的数。

输出格式 输出仅一个整数，为 a×b 矩阵中所有 n×n 正方形区域中的最大整数和最小整数的差值的最小值。

数据范围 2≤a,b≤1000,n≤a,n≤b,n≤100,矩阵中的所有数都不超过 10^9。

输入样例：

5 4 2
1 2 5 6
0 17 16 0
16 17 2 1
2 10 2 1
1 2 2 2

输出样例：

1

二、解题思路

二维滑动窗口模板题

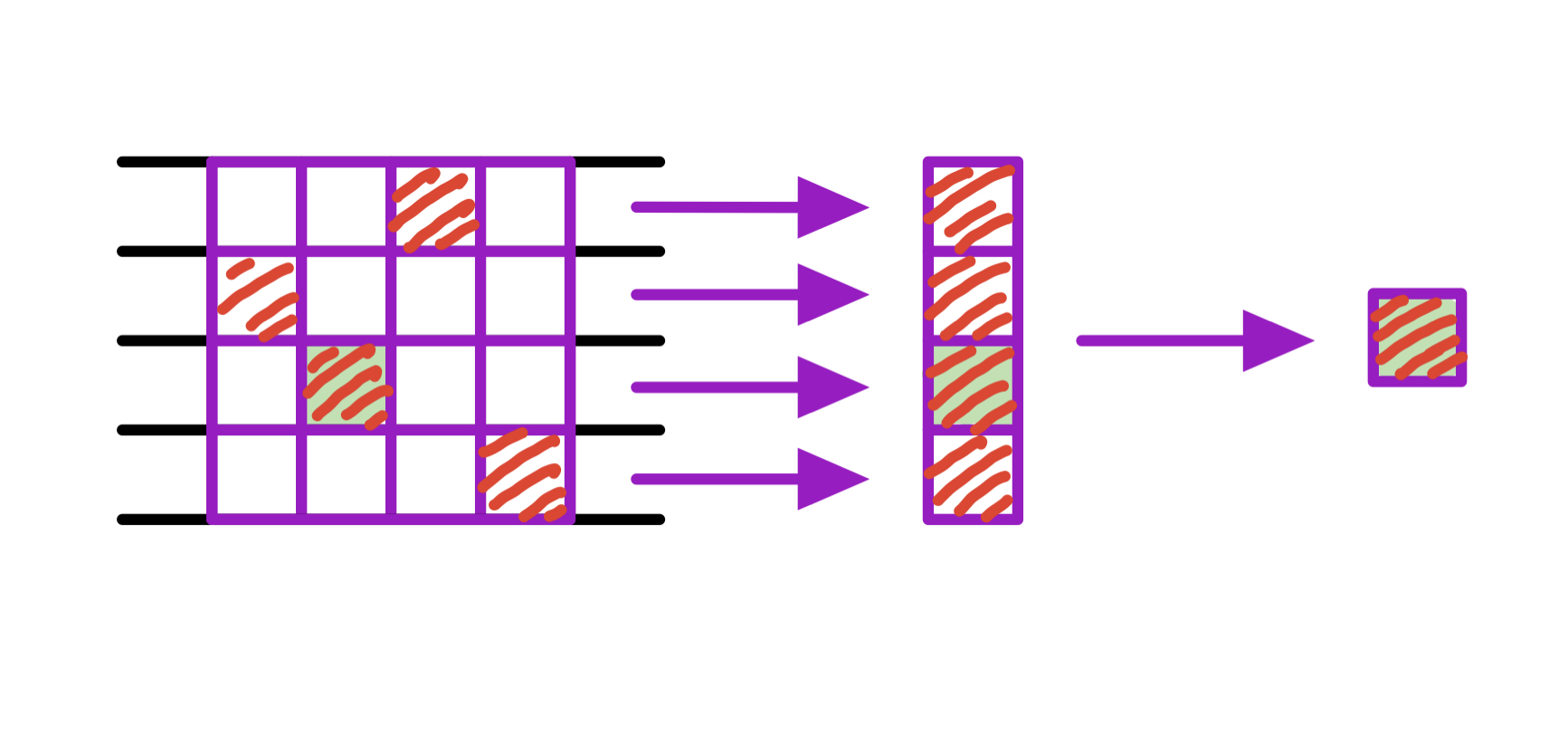
考虑求一个 二维 的 最值问题，我们可以把它转化为 一维 的 最值问题：

图中 红色阴影 格为该 行中 的 最值元素，绿色背影色 格为整个矩阵的 最值元素

由常见公式 max\{a,b,c,d\}=max\{max(a,b),max(c,d)\} 可知：

我们可以预处理出每 列 的行中 最值，再对该列求一个 最值，就是该 子矩阵 的 最值

该 降维手段，使得一个 二维滑动窗口问题 变成了 n行+n列 的 一维滑动窗口问题

而 一维滑动窗口 我们可太熟悉了，直接套 单调队列 的模板即可

三、暴力版本

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
const int INF = 0x3f3f3f3f;

int n;       // n行
int m;       // m列　
int k;       // 区间长度为k
int w[N][N]; // 原矩阵

// 暴力法，TLE
// 通过了 4/10个数据

/**
 * 模板函数，需记忆
 * 1、处理的是一维数组a[],保存的是一维数组b[]
 * 2、之所以使用一维数组，其实本质上是把二维数组拆开每一行，当作一维数组进行处理
 * 3、C++函数参数中传递一维数组，是不知道数组长度的，必须同时传输col,表示a[],b[]一共多少列
 * 4、这个函数用句人话描述就是：把一个一维数组的长度为K区间内的最小值都算出来，放到row_min这个数组中去。比如：k=3,row_min[5]=2,就是表示原数组[3,4,5]下标内，最小值是2
 */
void get_min(int a[], int b[], int col) {
    for (int i = 1; i <= col; i++) { // 枚举每一列
        b[i] = INF;
        // 找出每个数字包含[自己+前面]共k个范围内的最小值
        //  j的含义：指针，从i开始，向前倒k个 j∈[i-k+1,i]
        //  举栗子：i=10,k=2,则应该是[9,10]；如果i=1,k=2,则j只能取数值[1]，即j>0
        for (int j = i; j > max(i - k, 0); j--) b[i] = min(b[i], a[j]);

        // 注：这个循环，还是倒序方便些，正序的反倒是代码长度更长
        // for (int j = max(i - k + 1, 1); j <= i; j++) b[i] = min(b[i], a[j]);
    }
}

void get_max(int a[], int b[], int col) {
    for (int i = 1; i <= col; i++) { // 枚举每一列
        b[i] = -INF;
        for (int j = i; j > max(i - k, 0); j--) b[i] = max(b[i], a[j]);
    }
}

int main() {
    cin >> n >> m >> k; // n*m矩阵,找出k*k的正方形区域
    // 读入
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> w[i][j];

    /*步骤I：遍历每一行，完成最小值、最大值的向右转储，分别记录到row_min、row_max两个数组中。
    这两个数组，只是一个中间的状态，是为了给步骤II“竖着计算k个范围内的极大极小值”提供垫脚石
    */
    int row_min[N][N]; // 最小值
    int row_max[N][N]; // 最大值
    for (int i = 1; i <= n; i++) {
        get_min(w[i], row_min[i], m); // 填充每一行的,k个长度的区间内最小值 保存到row_min数组中, 注意：这并不是指某一个最小值，而是从k~m的所有长度够k个长度的区间极小值
        get_max(w[i], row_max[i], m); // 填充每一行的,k个长度的区间内最大值 保存到row_max数组中, 注意：这并不是指某一个最大值，而是从k~m的所有长度够k个长度的区间极大值
    }

    int t[N]; // 列转行，用到的临时中转数组
    int a[N]; // 最小值数组
    int b[N]; // 最大值数组

    /*
    步骤II:将竖向的区间极值向右下角归并
      (1)、依托row_min，对每一列进行列转行，保存为t
      (2)、利用get_min 将t数组再次存储为a数组
      (3)、此a数组，就是左归右，上归下的，边长为k的矩形中的最小值　

      (4)、依托row_max，对每一列进行列转行，保存为t
      (5)、利用get_max 将t数组再次存储为b数组
      (6)、此b数组，就是左归右，上归下的，边长为k的矩形中的最大值　
    */
    int res = INF; // 预求最小，先设最大

    for (int j = k; j <= m; j++) { // 捋着列来

        for (int i = 1; i <= n; i++) t[i] = row_min[i][j]; // 同一列的每一行，抄出来放到临时数组t中
        get_min(t, a, n);                                  // 对t这个临时数组，进行求k个范围内的最小值，将结果保存到a数组中

        for (int i = 1; i <= n; i++) t[i] = row_max[i][j]; // 同一列的每一行，抄出来放到临时数组t中
        get_max(t, b, n);                                  // 对t这个临时数组，进行求k个范围内的最大值，将结果保存到b数组中

        // 区域最大值-区域最小值，注意需要从k开始，前面的不够资格
        for (int i = k; i <= n; i++) res = min(res, b[i] - a[i]);
    }
    // 输出
    cout << res << endl;
    return 0;
}

四、单调队列优化

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
const int INF = 0x3f3f3f3f;

int n, m, k;
int w[N][N];
int row_min[N][N], row_max[N][N];
int q[N];

// 先想清楚get_min的意义：对于每个一维数组中的数字，找出包括它自己在内，长度最长为k的范围内，最小值是多少
// 这是一个典型的单调队列问题，窗口长度为k,包含自己在内

void get_min(int a[], int b[], int col) {
    int hh = 0, tt = -1; // 和前缀和相关的，才会有哨兵。这里和前缀和没关系，不用加入哨兵。
    for (int i = 1; i <= col; i++) {
        // 举栗子：比如i=5,k=3,则窗口范围是[3,4,5],也就是最远的队头元素下标是i-k+1,再比它小就不行了
        while (hh <= tt && q[hh] <= i - k) hh++;
        while (hh <= tt && a[q[tt]] >= a[i]) tt--; // 赶走比我老，但值还比我大的那些老家伙
        q[++tt] = i;
        // 此处需要包括i本身，所以在添加到队列后进行计算
        b[i] = a[q[hh]];
    }
}

void get_max(int a[], int b[], int col) {
    int hh = 0, tt = -1;
    // 和前缀和相关的，才会有哨兵。这里和前缀和没关系，不用加入哨兵。
    for (int i = 1; i <= col; i++) {
        while (hh <= tt && q[hh] <= i - k) hh++;
        while (hh <= tt && a[q[tt]] <= a[i]) tt--;
        q[++tt] = i;
        // 此处需要包括i本身，所以在添加到队列后进行计算
        b[i] = a[q[hh]];
    }
}

int main() {
    cin >> n >> m >> k;
    // 读入
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> w[i][j];

    /*步骤I：遍历每一行，完成最小值、最大值的向右转储，分别记录到row_min、row_max两个数组中。
    这两个数组，只是一个中间的状态，是为了给步骤II“竖着计算k个范围内的极大极小值”提供垫脚石的
    */
    int row_min[N][N]; // 最小值
    int row_max[N][N]; // 最大值
    for (int i = 1; i <= n; i++) {
        get_min(w[i], row_min[i], m); // 填充每一行的,k个长度的区间内最小值 保存到row_min数组中, 注意：这并不是指某一个最小值，而是从k~m的所有长度够k个长度的区间极小值
        get_max(w[i], row_max[i], m); // 填充每一行的,k个长度的区间内最大值 保存到row_max数组中, 注意：这并不是指某一个最大值，而是从k~m的所有长度够k个长度的区间极大值
    }

    int t[N]; // 列转行，用到的临时中转数组
    int a[N]; // 最小值数组
    int b[N]; // 最大值数组

    /*
    步骤II:将竖向的区间极值向右下角归并
      (1)、依托row_min，对每一列进行列转行，保存为t
      (2)、利用get_min 将t数组再次存储为a数组
      (3)、此a数组，就是左归右，上归下的，边长为k的矩形中的最小值　

      (4)、依托row_max，对每一列进行列转行，保存为t
      (5)、利用get_max 将t数组再次存储为b数组
      (6)、此b数组，就是左归右，上归下的，边长为k的矩形中的最大值　
    */
    int res = INF; // 预求最小，先设最大

    for (int j = k; j <= m; j++) { // 捋着列来

        for (int i = 1; i <= n; i++) t[i] = row_min[i][j]; // 同一列的每一行，抄出来放到临时数组t中
        get_min(t, a, n);                                  // 对t这个临时数组，进行求k个范围内的最小值，将结果保存到a数组中

        for (int i = 1; i <= n; i++) t[i] = row_max[i][j]; // 同一列的每一行，抄出来放到临时数组t中
        get_max(t, b, n);                                  // 对t这个临时数组，进行求k个范围内的最大值，将结果保存到b数组中

        // 区域最大值-区域最小值
        for (int i = k; i <= n; i++) res = min(res, b[i] - a[i]);
    }
    // 输出
    cout << res << endl;
    return 0;
}