python

5.1 KiB

Raw Permalink Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

`AcWing` `1089` . 烽火传递

一、题目描述

烽火台是重要的军事防御设施，一般建在交通要道或险要处。

一旦有军情发生，则白天用浓烟，晚上有火光传递军情。

在某两个城市之间有 n 座烽火台，每个烽火台发出信号都有一定的代价。

为了使情报准确传递，在连续 m 个烽火台中至少要有一个发出信号。

现在输入 n,m 和每个烽火台的代价，请计算在两城市之间 准确传递情报所需花费的总代价最少 为多少。

输入格式 第一行是两个整数 n,m，具体含义见题目描述；

第二行 n 个整数表示每个烽火台的代价 a_i。

输出格式 输出仅一个整数，表示最小代价。

数据范围 1≤m≤n≤2×10^5,0≤a_i≤1000

输入样例：

5 3
1 2 5 6 2

输出样例：

###　二、题目解析

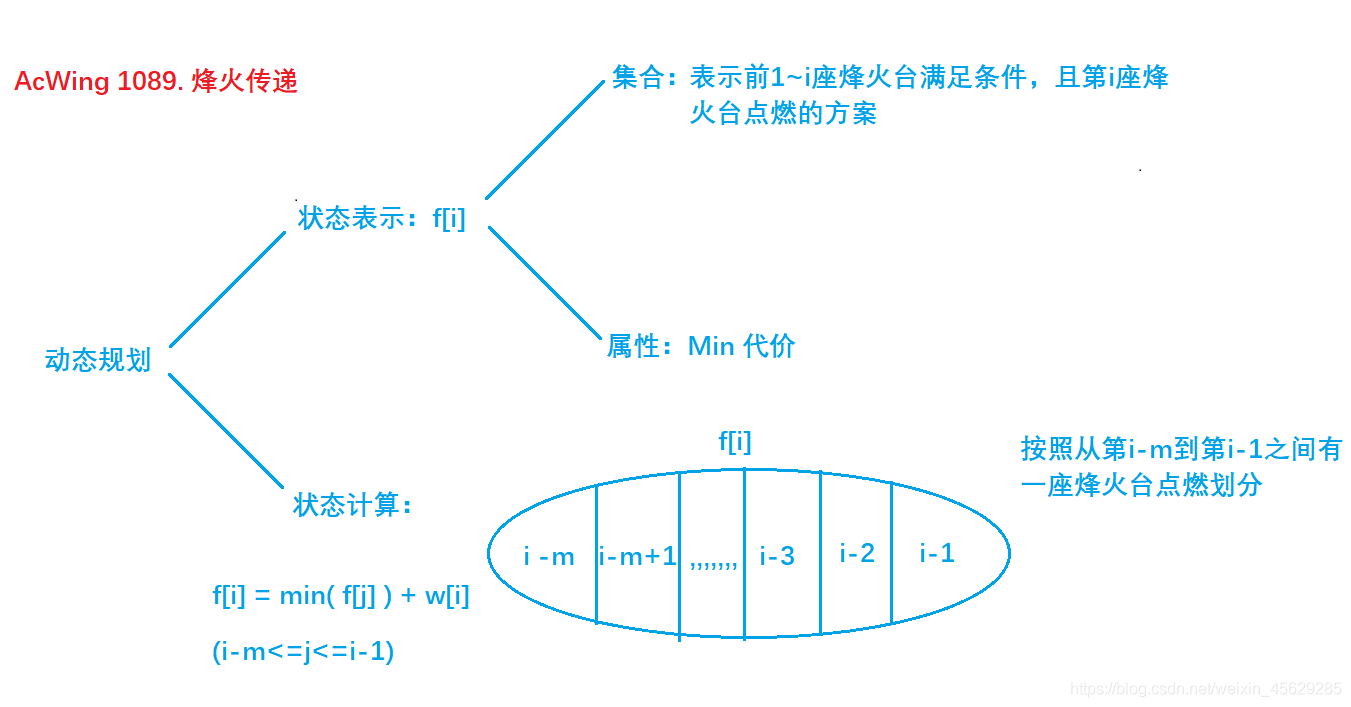
状态表示

f[i]:前1 \sim i座烽火台满足条件，且第i座烽火台点燃的方案集合

属性

所有符合条件的方案集合中的 最小代价值

状态计算

如何划分集合？

题目要求在连续 m个烽火台中至少要有一个发出信号，即连续的m个烽火台中至少要有一个被点燃。而f[i]表示的含义中，第i座已经被点燃，因此在第i座向前的前m座烽火台至少要有一个被点燃。被点燃的可以是i-m, i-m+1,...,i-2,i -1

故状态计算方程：

\large f[i] = min(f[j]) + w[i]\  j \in [i-m,i-1]

一段区间的最值可以用单调队列求解。

此题中，我们定义一个单调递增队列，队列中维护的是f[j]的最小值集合,每次拿出队头元素，即长为m的区间中，值最小的f[j]来更新答案。

\large Q:有个疑问，为什么状态表示时，要将第i座表示为点燃？

我们可以 从问题出发，每m座烽火台中必然要有一座要被点燃。那么最后n座烽火台同样也是如此。如果我们将f[i]定义为前1\sim i座烽火台满足条件，且第i座烽火台点燃的方案集合,那么答案一定在 f[n-m+1],f[n-m+2],...,f[n]之间产生,也就是说将第i座表示为点燃可以很容易表示出答案。这就给我们一个启发，在定义状态表示时，一定要考虑定义的状态是否可以包含答案。

三、`DP`+暴力查找最小值

j = max(0, i - m)

上面这句话需要注意一下，别整出下标是负数的。说句人话就是:“一个看一个，个个向前看，最远能看m个，不够m个有多少算多少。”

#include <bits/stdc++.h>

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 200010;
int f[N];
int w[N], n, m;

//  通过了 11/12个数据
int main() {
    /**
    普通DP大法
    状态表示：
     ①集合:f[i]表示前i个灯塔满足条件，并且i点亮。
     ②属性：最小代价
    状态计算：f[i]=min(f[j]+w[i]) (i−m≤j≤i−1)
    答案：(n−m+1)~n必须有灯塔亮，所以枚举一下求出最小值即可
    */
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> w[i];

    //初始化
    memset(f, 0x3f, sizeof f);              //预求最小，先设最大
    f[0] = 0;                               //需要手动初始化一下递推的base case
    //依题意，f[1]代表第1个灯塔点亮需要付出的代价是w[1],也就是f[0]=0,想想也正常，虚拟第0个点亮成本为0~
    for (int i = 1; i <= n; i++)
        for (int j = max(0, i - m); j <= i - 1; j++)    //向前查看它之前的m个
            f[i] = min(f[i], f[j] + w[i]);

    int res = INF;
    for (int i = n + 1 - m; i <= n; i++) res = min(res, f[i]);
    printf("%d\n", res);
    return 0;
}

四、单调队列优化

#include <bits/stdc++.h>

using namespace std;

const int N = 200010;
const int INF = 0x3f3f3f3f;
int f[N];
int w[N], n, m;
int q[N], hh, tt;

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> w[i];
    hh = 0, tt = 0, q[0] = 0;

    for (int i = 1; i <= n; i++) {
        // 滑动窗口在i左侧，不包括i,使用前序信息可以更新f[i]，滑动窗口长度最长为m
        while (hh <= tt && i - q[hh] > m) hh++;

        // 因为i不在滑动窗口中，需要用滑动窗口的内容更新f[i]，在while上方更新
        f[i] = f[q[hh]] + w[i];

        // i入队列
        while (hh <= tt && f[q[tt]] >= f[i]) tt--;
        q[++tt] = i;
    }
    // 答案可能存在于 n-1,n-2,...n-m+1中，枚举一下求最小值即可
    int res = INF;
    for (int i = n + 1 - m; i <= n; i++) res = min(res, f[i]);
    printf("%d\n", res);
    return 0;
}

5.1 KiB Raw Permalink Blame History Unescape Escape

AcWing 1089 . 烽火传递