5.6 KiB
一、题目描述
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|。
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围
1≤n≤10^5,1≤m≤2∗10^5,
图中涉及边的边权的绝对值均不超过 1000。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6
二、Kruskal算法
1、基本思路:
(1) 将所有边按权重从小到大排序
(2) 枚举每条边 a \sim b ,权重是c
if a,b不在一个集合中 :
将这条边加入集合中
结束
2、与prim算法的区别
- 克鲁斯卡尔算法的基本思想是以边为主导地位,普利姆算法是以点为主导的地位的。
prim算法适合稠密图,kruskal算法适合稀疏图。理由也挺简单的,kruskal是按边存的,边少就合适,边多就不适合。稀疏图当然边少,稠密图是点少,但边多,边可能达到节点数的平方,即每个节点都与其它节点有边。
3、算法模拟
假如有以下几个城市,之间都有相连的道路:
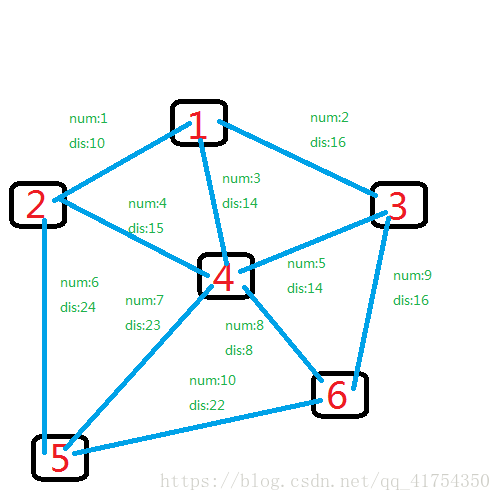
根据kruskal的原理,我们需要对边权dis进行排序,每次找出最小的边。
排序后,最小的边自然是第8条边,于是4和6相连。

遍历继续,第二小的边是1号,1和2联通。
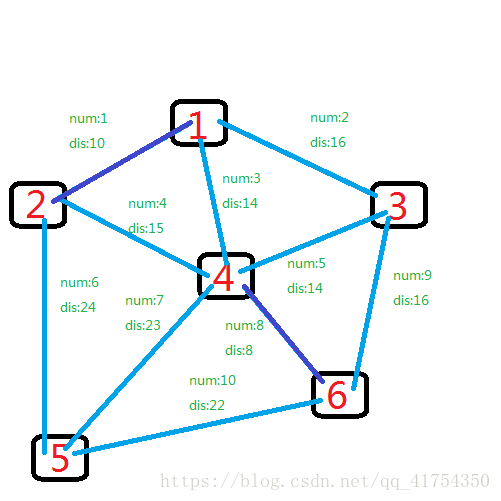
再后来是边3连接1,4。
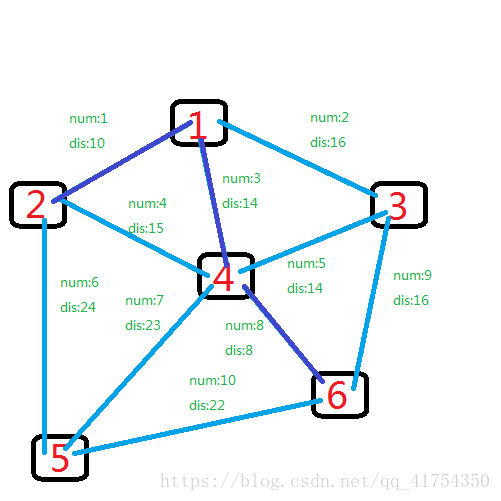
dis也是14的还有边5,它连接3,4。
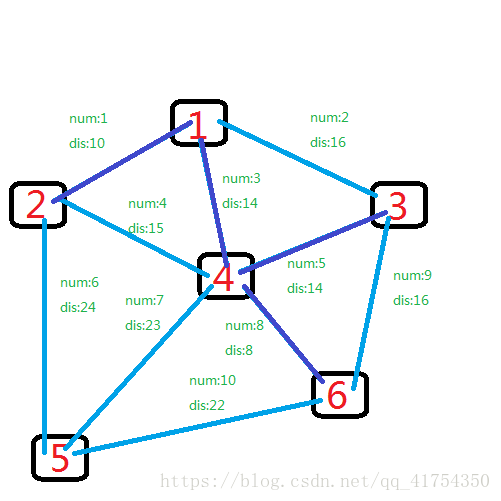
其次是dis为15的边4,但是2和4已经相连了,pass。
然后是dis为16的两条边(边2和边9),边2连接1和3,边9连接3和6,它们都已经间接相连,pass。
再然后就是dis为22的边10,它连接5和6,5还没有加入组织,所以使用这边。继续,发现此时已经连接了n-1条边,结束,最后图示如下:

本题与 https://www.acwing.com/problem/content/839/ 是姊妹题,其实Kruskal算法就是一个并查集的应用。
不像Prim算法,不用考虑边界,考虑循环N次啊,计算最小值啊,还要用堆进行优化啊,这个就是一个并查集,思路简单。
4、疑问与解答
Q:只需要简单结构体即可,不需要邻接表或者邻接矩阵来存,为什么呢?
A:之所以使用邻接表或邻接矩阵,其实说白了,是按点存的,记录A点和B点的关系。用结构体存储,其实是按边存的,就是题目说有一条A-B的边(权为C),我们就存了一个A-B权为C的边。
按点存麻烦(邻接表或邻接矩阵),按边存(结构体数组)简单。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = N << 1;
const int INF = 0x3f3f3f3f;
int n, m; // n条顶点,m条边
int res; // 最小生成树的权值和
int cnt; // 最小生成树的结点数
// Kruskal用到的结构体
struct Node {
int a, b, c;
bool const operator<(const Node &t) const {
return c < t.c; // 边权小的在前
}
} edge[M]; // 数组长度为是边数
// 并查集
int p[N];
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// Kruskal算法
void kruskal() {
// 1、按边权由小到大排序
sort(edge, edge + m);
// 2、并查集初始化
for (int i = 1; i <= n; i++) p[i] = i;
// 3、迭代m次
for (int i = 0; i < m; i++) {
int a = edge[i].a, b = edge[i].b, c = edge[i].c;
a = find(a), b = find(b);
if (a != b)
p[a] = b, res += c, cnt++; // cnt是指已经连接上边的数量
}
// 4、特判是不是不连通
if (cnt < n - 1) res = INF;
}
int main() {
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
edge[i] = {a, b, c};
}
kruskal();
if (res == INF)
puts("impossible");
else
printf("%d\n", res);
return 0;
}