5.3 KiB
一、题目描述
Palmia国有一条横贯东西的大河,河有笔直的南北两岸,岸上各有位置各不相同的N个城市。
北岸的每个城市有且仅有一个友好城市在南岸,而且不同城市的友好城市不相同。
每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市,但是由于河上雾太大,政府决定避免任意两条航道交叉,以避免事故。
编程帮助政府做出一些批准和拒绝申请的决定,使得在保证任意两条航线不相交的情况下,被批准的申请尽量多。
输入格式
第1行,一个整数N,表示城市数。
第2行到第n+1行,每行两个整数,中间用1个空格隔开,分别表示南岸和北岸的一对友好城市的坐标。
输出格式
仅一行,输出一个整数,表示政府所能批准的最多申请数。
数据范围
1≤N≤5000,0≤x_i≤10000
输入样例:
7
22 4
2 6
10 3
15 12
9 8
17 17
4 2
输出样例:
4
二、题目分析
要求
-
每个城市只能建立一座桥
-
所有桥与桥之间不能有交叉
目标
最多能建立多少座桥
图解
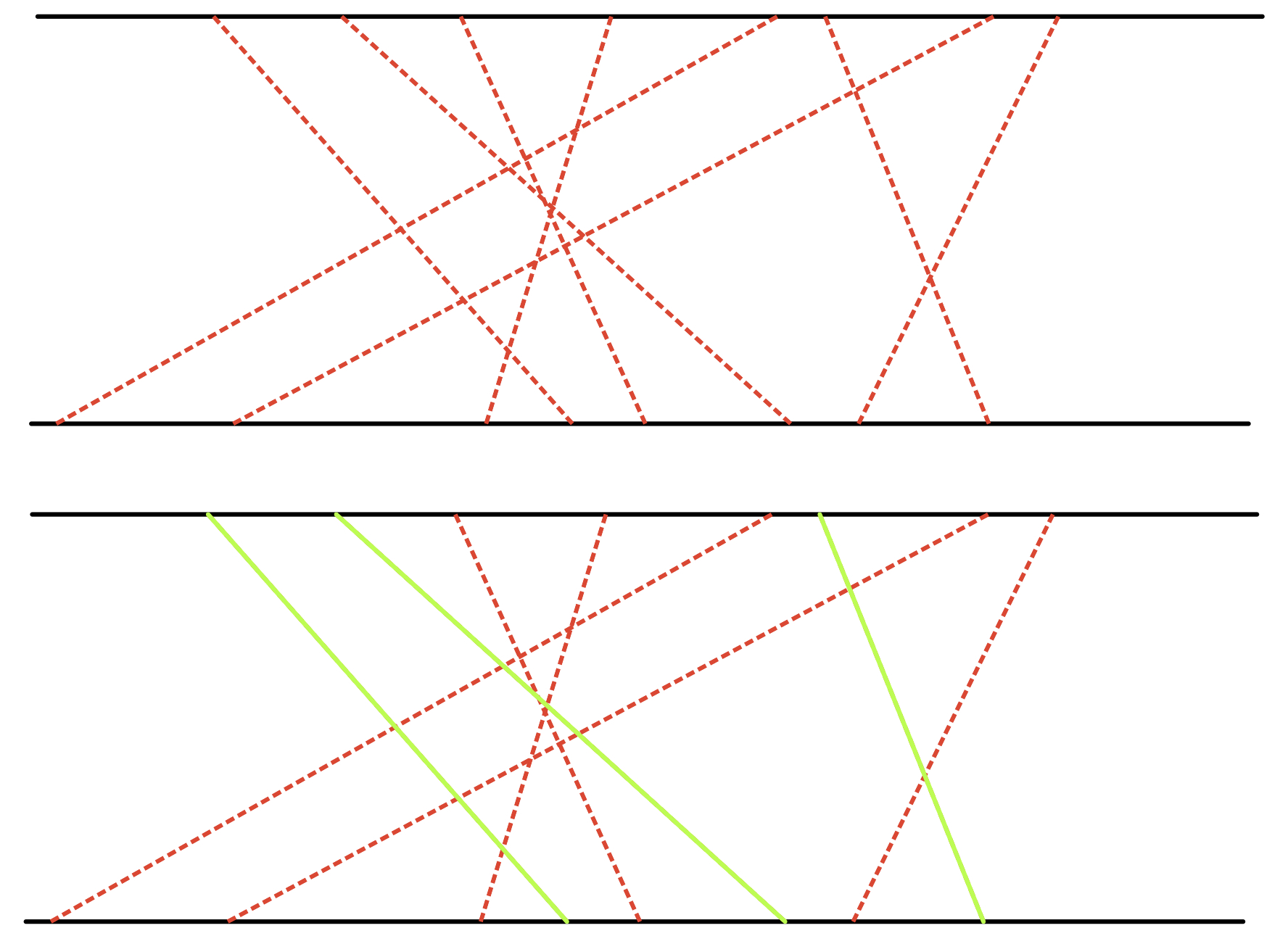
1、什么情况会交叉?
手动模拟可知:当两座桥对应的两对城市((x_1,y_1),(x_2,y_2))出现了下面的情况:
\large \left\{\begin{matrix}
x_1>x_2 \ \&\& \ y_1<y_2 & \\
x_1<x_2 \ \&\& \ y_1>y_2 &
\end{matrix}\right.
注:
x_1 \neq x_2 ,y_1 \neq y_2是显然的,同岸的城市不能堆在一起吧~
结论:
数对的坐标 逆序 关系将导致出现桥交叉
2、暴力怎么做?
-
如果按照暴力的思路去思考的话,因为每座桥都可以选择建或者不建两种情况,所以要枚举所有的可能性,需要枚举的次数为
2^N,其中N≤5000,肯定会TLE啊,需要优化。 -
如果暴力,需要枚举每一个友好城市的坐标!,既然要枚举坐标,是不是得排个序,从小到大讨论,要不逆序不逆序怎么判断?
当你想到需要把一端坐标从小到大排序时,就马上会想到,那另一端怎么办?对应关系不能丢失啊,所以,需要使用
pair<int,int>进行处理。
到这,似乎快看到曙光: 一端顺序由小到大,讨论另一端,怎么样才能让在没有交叉的情况下桥的数量还最多呢?当然是升序的序列越长越好,转化为求LIS问题了!
#### 3、总结
-
多个数对的问题,套路:对数对的第一维排序,再处理第二维。这样操作,可以起到类似于 降维 的作用,使问题简化。
-
本题还是有一些思维的难度,需要对问题进行转化。用 数对 描述问题比较好想,为什么要按左端点进行排序呢?似乎对于数对而言,大多数情况需要固定一个端点,比如区间合并,如果我们能想到这是一个用数对描述的问题,不妨先想一下是不是在按左端点排序一下。
-
按左端点排序后,一般的思路就是对比右端点(要不按左端点排序就没啥意义了~)。此时就是 把二维的概念转化为一维的概念。本题是根据右端点的逆序关系来说明当前路线与前序的矛盾关系。
三、O(N^2)实现代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second
const int N = 5010;
PII a[N]; // 南岸和北岸的一对友好城市的坐标
int f[N]; // 记录以f[i]为结尾的一对友好城市时的,不产生交叉的最多城市对数
int n; // n组友好城市
int res;
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i].x >> a[i].y;
sort(a + 1, a + 1 + n); // PII默认按第一维度first进行排序
// LIS
for (int i = 1; i <= n; i++) {
f[i] = 1;
for (int j = 1; j < i; j++)
if (a[i].y > a[j].y)
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
}
printf("%d\n", res);
return 0;
}
四、O(NlogN)实现代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second
const int N = 5010;
PII a[N]; // 南岸和北岸的一对友好城市的坐标
int f[N], fl; // 数组模拟栈
int n; // n组友好城市
int res;
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i].x >> a[i].y;
sort(a + 1, a + 1 + n);
f[++fl] = a[1].y;
for (int i = 2; i <= n; i++) {
if (a[i].y > f[fl])
f[++fl] = a[i].y;
else
*lower_bound(f + 1, f + 1 + fl, a[i].y) = a[i].y;
}
printf("%d\n", fl);
return 0;
}
五、关键字
- 转化模型
- 数对
- 排序 (第一维)
LIS(第二维)