python/TangDou/AcWing/LCA/1172.md

AcWing 1172 祖孙询问

一、题目描述

给定一棵包含 n 个节点的有根无向树，节点编号互不相同，但不一定是 1 \sim n。

有 m 个询问，每个询问给出了一对节点的编号 x 和 y，询问 x 与 y 的祖孙关系。

注：找出多对节点的祖孙关系，不是一对

输入格式 输入第一行包括一个整数 表示节点个数；

接下来 n 行每行一对整数 a 和 b，表示 a 和 b 之间有一条无向边。如果 b 是 −1，那么 a 就是树的根；

第 n+2 行是一个整数 m 表示询问个数；

接下来 m 行，每行两个不同的正整数 x 和 y，表示一个询问。

输出格式 对于每一个询问，若 x 是 y 的祖先则输出 1，若 y 是 x 的祖先则输出 2，否则输出 0。

数据范围 1≤n,m≤4×10^4, 1≤每个节点的编号≤4×10^4

输入样例：

10
234 -1
12 234
13 234
14 234
15 234
16 234
17 234
18 234
19 234
233 19
5
234 233
233 12
233 13
233 15
233 19

输出样例：

1
0
0
0
2

二、最近公共祖先

（Least Common Ancestor）,简称LCA。

在一颗有根树中, 每个节点向上追溯都有一系列祖宗节点. 对于任意两个节点, 在它们祖宗节点的交集中离它们最近的节点称为它们的 最近公共祖先。

注意: 节点本身也可作为其祖先节点.

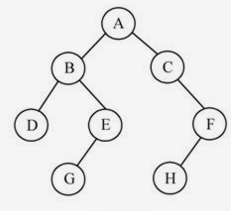
比如上图中的D点和G点的最近公共祖先节点就是B点。下面介绍求解LCA问题的两种基本方法：

向上标记法

我们自己是如何判断LCA的呢？两只眼睛同时从D点和G点往上追溯，很快就可以定位到B点。计算机向上回溯自然不是问题，但是并不能很快的判断出回溯过程中最先相交于哪一点，因此只能 异步 的执行节点的回溯。首先D向上追溯到B点、A点，做好访问标记；然后G点向上追溯到E点，再往上到B点发现已经做好标记了，于是B点就是LCA节点。这种求解LCA的办法被称为 向上标记法 ，由其中一个节点向上走到根节点并做好标记，另一个节点再往上走的时候第一次遇见的已标记的节点就是最近公共祖先节点。向上标记法过程相当简单，书上说其复杂度是O(n)，即正比于树上节点的规模。其实该算法的复杂度用O(h)，也就是 树高 来衡量更加准确。

树上倍增法

向上标记法看似简单高效，求上图中D和G的LCA固然很快，但是如果要 求多对节点 的LCA呢？比如求D、E的，求G、H的，...，我们会发现G点向上走的时候标记了其祖先节点，然后E向上走又会标记一遍祖先节点，向上回溯的路径大都是相同的，这就 存在很大的冗余。

如果 同步 的向上回溯会怎样呢？预处理 下每个节点向上回溯任意步后的位置，记录下来，然后用某种算法快速的求出两个节点的LCA。

最先遇见的困难就是节点u和节点v离他们的LCA节点的 深度差不同。

如果 两个节点处于同一深度，比如G和H点，深度都是3，我们完全可以 二分答案 了:先判断下G和H向上两步是不是到达了同一个节点，如果没到达，就向上四步。如果两个节点是处于同一深度的，我们在预处理节点向上走若干步的信息后，就可以在O(log_2h)的时间内求出LCA了。

当然既可以使用二分求解也可以使用 倍增求解，两个节点同时向上 走 1,2,4,8,...步判断是否到达了同一点。那么我们在后面为什么要选择倍增而不是二分呢？这又是个问题。到这里我们其实已经不知不觉的理解了树上倍增法的第一个重要的步骤: 将两个节点调整到同一深度上。比如求u和v的LCA，u的深度是10，v的深度是6，首先求出u向上回溯到深度为6的祖先节点u_1，如果u_1就是v点，那么LCA就是v，否则继续求u_1和v的LCA。此时就是求处于同一深度的两个节点的LCA了，就十分方便了。所以 树上倍增法 无非就是先将深度大的节点调整到与深度小的节点同一深度（向上回溯），然后继续求LCA。

再回到开头说的 预处理出所有节点向上回溯若干步的节点，这是十分没有必要的 。我们只需要 预处理出每个节点向上回溯2的倍数步的节点 就可以满足我们所有的需要了。比如要回溯11步，完全可以先走8步，再走2步，再走1步，任何十进制整数肯定是可以转化为二进制表达的，11 = (1011)_2，二进制拆分的思想足以让我们走到任意的地方。

为什么是先走步数最大的再逐步缩小步数，而不是先1再2再8呢？ 因为二进制拆分实现过程中并不需要我们真的去拆分11，我们可以先尝试迈出一个很大的步数，比如16，发现比11大，于是迈出8步，再尝试迈出4步，发现又超过11了，于是迈出2步，最后迈出1步，这是个不断尝试便于实现的倍增过程。调整到同一深度的两个节点需要再次使用倍增的方法求LCA，比如先判断下两个节点向上回溯8步的节点是不是同一个，是就说明LCA不会在更高的位置了，于是重新判断向上回溯4步的是不是同一个，如果不是，则说明LCA还在上面，再对这个迈出4步的两个节点继续向上回溯2步，直至两个节点的父节点就是LCA为止。

算法实现

f[i][k]:节点i向上回溯2^k步的节点标号

边界情况f[i][0]表示i的 父节点。

f数组的求解就是使用倍增法常用的动态规划公式了，要想求出i向上走2^k步的节点，只需要先求出i向上走2^{k-1}步的节点j，然后再求j向上走2^{k-1}步的节点即可。状态转移方程:

\large f[i][k] = f[f[i][k-1]][k-1]

预处理 可以在bfs遍历树的过程中实现，同时记录下所有节点的深度depth。

void bfs(int root) {
    //根结点的深度为1
    depth[root] = 1;
    queue<int> q;
    q.push(root);
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = h[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (!depth[v]) {
                depth[v] = depth[u] + 1; //记录每个节点的深度
                q.push(v);
                f[v][0] = u; // f[v][0]表示v的父节点
                //因为bfs的特性，所以在计算f[v][k]时，前序依赖数据
                // f[v][k - 1],f[f[v][k - 1]][k - 1]肯定已经被填充过
                for (int k = 1; k <= 20; k++)
                    f[v][k] = f[f[v][k - 1]][k - 1];
            }
        }
    }
}

初始情况下将所有节点的深度设置为0，所以一旦从u可以走到v并且v的深度没有被标识过，就说明u是v的父节点，同时可以更新v的深度了(无向图，防止v->u走回头路)。我们知道bfs遍历树的过程是层序遍历，遍历到v时v的祖先节点的信息都已经被预处理过了，所以此时 f[v][k] = f[f[v][k - 1]][k - 1]中的f[v][k-1]一定已经求出来了。

倍增代码

//最近公共祖先
int lca(int a, int b) {
    // a保持深度更大，更下面
    if (depth[a] < depth[b]) swap(a, b);
    // 深度对齐
    for (int k = 15; k >= 0; k--)
        if (depth[f[a][k]] >= depth[b]) a = f[a][k];

    //如果a,b是同一个点了，则LCA找到
    if (a == b) return a;
    
    //倍增查找,向结果逼近
    for (int k = 15; k >= 0; k--)
        if (f[a][k] != f[b][k])
            a = f[a][k], b = f[b][k];
    //返回结果
    return f[a][0];
}

如果a深度大于b，就交换a、b节点 ，从而保持a节点一直在下面。然后就是按照上面所说的 倍增 的操作二进制拆分调整b到与a同一深度，如果两点重合，LCA就是a点。否则，继续对a、b向上倍增求LCA，最后的结果为什么是a的父节点呢？这是因为倍增的终点就是a和b调整到LCA节点的下一层。举个例子，比如a和b离LCA有6步，首先a和b都向上走4步，然后想向上走2步发现此时两点重合了，于是只走一步，此时倍增终止，a和b离LCA恰好是一步之遥。

解释：

for (int k = 15; k >= 0; k--)
       if (f[a][k] != f[b][k])
           a = f[a][k], b = f[b][k];

这里的条件是不相等的才赋值吧？最后a，b是不等的。也就是它俩的处在等、不等的临界点的，现在是不等，再多一点点就是等，而多一点点其实就是 f[a][0],即父节点。

五、实现代码

#include <bits/stdc++.h>
using namespace std;
const int N = 40010, M = 80010;
// 邻接表
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int n;
int depth[N]; // 每个节点的深度
int f[N][16]; // 设f[i][k]表示节点i向上回溯2^k步的节点标号
// 预处理
//  1、每个点的深度
//  2、记录节点i向上回溯2^k步的节点标号
void bfs(int root) {
    queue<int> q;    // 声明队列，准备从根开始对整棵树进行宽搜
    q.push(root);    // 根节点入队列
    depth[root] = 1; // 根结点深度为1
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = h[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (!depth[v]) {             // 如果深度为0，表示没有访问过，防止走回头路
                depth[v] = depth[u] + 1; // 记录每个节点的深度
                f[v][0] = u;             // f[j][0]表示j跳2^0=1到达的是它的父节点
                q.push(v);               // 下一次该j发挥作用了
                /*举个栗子：
                j 向上跳 2^0=1,2^1=2,2^2=4,2^3=8,2^4=16,2^5=32,...步,
                分别记录这样跳到达的节点是什么编号，这样其实是按二进制思想记录的信息。
                f[j][k] = f[f[j][k - 1]][k - 1] 采用了递推的思路，比如i向上想走8级，现在向上走了4级到达了j,也可以继续从j出发向上再走4次，是一回事, 但由于这样利用了已有结果会更快
                因为bfs特性，在计算f[j][k]时，前序依赖数据已经被填充过，可以快速利用
                */
                for (int k = 1; k <= 15; k++) f[v][k] = f[f[v][k - 1]][k - 1];
            }
        }
    }
}
// 最近公共祖先
int lca(int a, int b) {
    // a保持深度更大
    if (depth[a] < depth[b]) swap(a, b);

    // 对齐a,b,跳冒不跳，跳少再跳
    for (int k = 15; k >= 0; k--)
        if (depth[f[a][k]] >= depth[b]) a = f[a][k];
        
    if (a == b) return a;

    // 同级，跳冒不跳，跳少再跳
    for (int k = 15; k >= 0; k--)
        if (f[a][k] != f[b][k])
            a = f[a][k], b = f[b][k];

    // a的父节点，就是lca(a,b)
    return f[a][0];
}
int main() {
    memset(h, -1, sizeof h);

    scanf("%d", &n);
    int a, b, m, root;

    for (int i = 0; i < n; i++) {
        scanf("%d %d", &a, &b);
        if (b == -1)
            root = a; // 找到根节点
        else
            add(a, b), add(b, a); // 无向树
    }
    // 预处理,生成倍增的下2^k级跳位置数据f[i][k]
    bfs(root);

    scanf("%d", &m);
    while (m--) {
        scanf("%d %d", &a, &b);
        int p = lca(a, b);
        if (p == a)
            puts("1");
        else if (p == b)
            puts("2");
        else
            puts("0");
    }
    return 0;
}

Q1:为什么上面实现代码中用的上限是16？

int res = 1;
for (int i = 1;; i++) {
    res *= 2;
    if (res > 4 * 1e4) {
        printf("%d\n", i);
        break;
    }
}

结果输出是16,题目中，当前节点i占了一层，它的父节点表示是f[i][0],所以，最多向上返2^{15}层

Q2：如果不写成16，写成20会怎么样？

k变大了，会跳到一个不存在的位置上去，代码显示跳到的是0号位置，而我们知道，一般这样的题目，都是要求从1 \sim N,避开了0号。

注意：如果真的想偷懒，不想仔细计算到底应该跳多少步，可以盲写成32,但要注意的是除了要把代码中所有16修改为32外，还要记得把f数组二维的大小改大，否则会WA,别问我怎么知道的~

f[19][0]=234 f[19][1]=0 f[19][2]=0 f[19][3]=0 f[19][4]=0 f[19][5]=0 f[19][6]=0 f[19][7]=0 f[19][8]=0 f[19][9]=0 f[19][10]=0 f[19][11]=0 f[19][12]=0 f[19][13]=0 f[19][14]=0 f[19][15]=0 
f[18][0]=234 f[18][1]=0 f[18][2]=0 f[18][3]=0 f[18][4]=0 f[18][5]=0 f[18][6]=0 f[18][7]=0 f[18][8]=0 f[18][9]=0 f[18][10]=0 f[18][11]=0 f[18][12]=0 f[18][13]=0 f[18][14]=0 f[18][15]=0 
f[17][0]=234 f[17][1]=0 f[17][2]=0 f[17][3]=0 f[17][4]=0 f[17][5]=0 f[17][6]=0 f[17][7]=0 f[17][8]=0 f[17][9]=0 f[17][10]=0 f[17][11]=0 f[17][12]=0 f[17][13]=0 f[17][14]=0 f[17][15]=0 
f[16][0]=234 f[16][1]=0 f[16][2]=0 f[16][3]=0 f[16][4]=0 f[16][5]=0 f[16][6]=0 f[16][7]=0 f[16][8]=0 f[16][9]=0 f[16][10]=0 f[16][11]=0 f[16][12]=0 f[16][13]=0 f[16][14]=0 f[16][15]=0 
f[15][0]=234 f[15][1]=0 f[15][2]=0 f[15][3]=0 f[15][4]=0 f[15][5]=0 f[15][6]=0 f[15][7]=0 f[15][8]=0 f[15][9]=0 f[15][10]=0 f[15][11]=0 f[15][12]=0 f[15][13]=0 f[15][14]=0 f[15][15]=0 
f[14][0]=234 f[14][1]=0 f[14][2]=0 f[14][3]=0 f[14][4]=0 f[14][5]=0 f[14][6]=0 f[14][7]=0 f[14][8]=0 f[14][9]=0 f[14][10]=0 f[14][11]=0 f[14][12]=0 f[14][13]=0 f[14][14]=0 f[14][15]=0 
f[13][0]=234 f[13][1]=0 f[13][2]=0 f[13][3]=0 f[13][4]=0 f[13][5]=0 f[13][6]=0 f[13][7]=0 f[13][8]=0 f[13][9]=0 f[13][10]=0 f[13][11]=0 f[13][12]=0 f[13][13]=0 f[13][14]=0 f[13][15]=0 
f[12][0]=234 f[12][1]=0 f[12][2]=0 f[12][3]=0 f[12][4]=0 f[12][5]=0 f[12][6]=0 f[12][7]=0 f[12][8]=0 f[12][9]=0 f[12][10]=0 f[12][11]=0 f[12][12]=0 f[12][13]=0 f[12][14]=0 f[12][15]=0 
f[233][0]=19 f[233][1]=234 f[233][2]=0 f[233][3]=0 f[233][4]=0 f[233][5]=0 f[233][6]=0 f[233][7]=0 f[233][8]=0 f[233][9]=0 f[233][10]=0 f[233][11]=0 f[233][12]=0 f[233][13]=0 f[233][14]=0 f[233][15]=0 

总结

LCA算法，本质就是一个二进制的拼凑组装大法,关键词如下：

• ① 深度
• ② 对齐
• ③ 倍增,二进制
• ④ 每个节点都记录信息
• ⑤ 尝试8,4,2,1
• ⑥ 动态规划
• ⑦ 差一步到LCA