9.8 KiB
AcWing 181. 回转游戏
一、题目描述
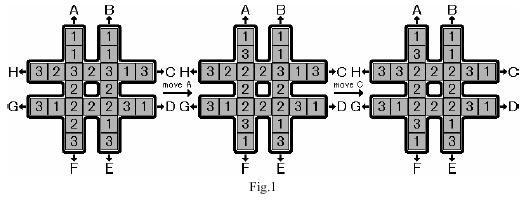
如下图所示,有一个 # 形的棋盘,上面有 1,2,3 三种数字各 8 个。
给定 8 种操作,分别为图中的 A∼H。
这些操作会 按照图中字母和箭头所指明的方向,把一条长为 7 的序列循环移动 1 个单位。
例如下图最左边的 # 形棋盘执行操作 A 后,会变为下图中间的 # 形棋盘,再执行操作 C 后会变成下图最右边的 # 形棋盘。
给定一个初始状态,请使用 最少的操作次数,使 # 形棋盘最中间的 8 个格子里的数字相同。
输入格式 输入包含多组测试用例。
每个测试用例占一行,包含 24 个数字,表示将初始棋盘中的每一个位置的数字,按整体从上到下,同行从左到右的顺序依次列出。
输入样例中的第一个测试用例,对应上图最左边棋盘的初始状态。
当输入只包含一个 0 的行时,表示输入终止。
输出格式 每个测试用例输出占两行。
第一行包含所有移动步骤,每步移动用大写字母 A∼H 中的一个表示,字母之间没有空格,如果不需要移动则输出 No moves needed。
第二行包含一个整数,表示移动完成后,中间 8 个格子里的数字。
如果有多种方案,则输出 字典序最小 的解决方案。
输入样例:
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0
输出样例:
AC
2
DDHH
2
二、题目解析
1、限定步数+目标
本题同样考察IDA*,每次有八种操作可以选择,一旦 一开始选择了错误的方向,便可能搜索到 很多无用的较深分支,所以,一开始最好别陷的太深,否则将无法自拔,多么深刻的人生哲理~,因此可以在 迭代加深的基础上使用估价函数。
分析 最终状态 ,最终状态是中间八个数都是同一个数字,而每次操作都会使得中间八个数中的一个数出去,外面的一个数进来,也就是改变中间的一个数字。设x是中间八个数的 众数,出现了k次,则至少要经过8-k次操作才能够把中间所有的数都变成x,这就是 估价函数的定义,即f = 8 - 众数 出现的次数。
基本框架 已经解决了,下面要解决的是如果 存储 和 操作 这个井字形棋盘。
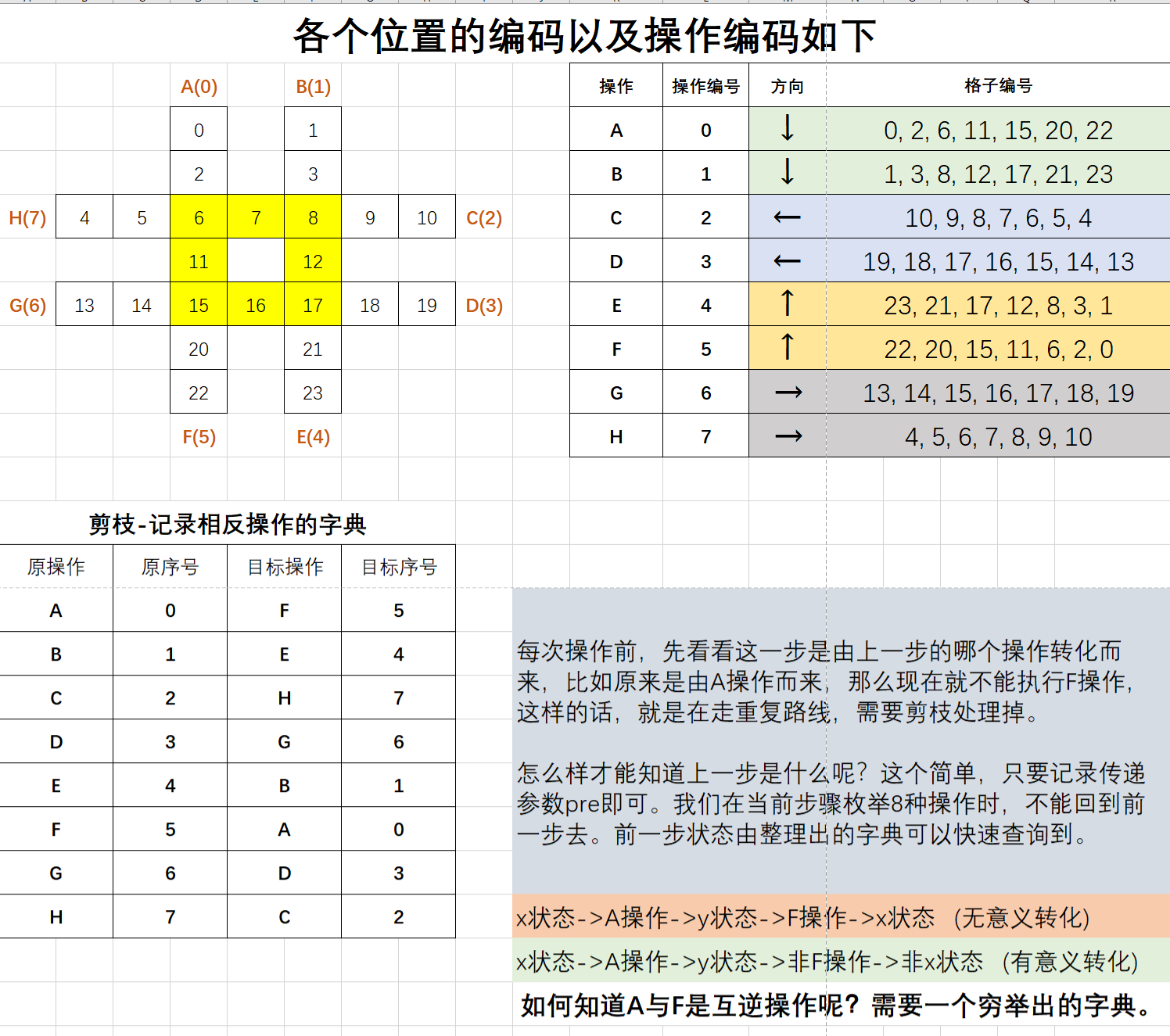
- 首先,按照题目的输入格式给这
24个数编号,得到下面的图:(题目的输入顺序就是如此)
-
用个二维数组
\large g存储 各种操作 会操作的数字,比如A会操作0,2,6,11,15,20,22,其他的也类似,得到一个八行七列的数组,每次操作只需要 将对应的数组第一个数搬到末尾 即可。 -
用
\large center[8]存储中间的8个数的下标 -
用
\large q存储编号0到23这24个数的具体数值 -
用
\large op数组存下各个操作的 反操作编号,每次操作前判断下不走回头路,dfs完恢复现场时也是用此次进行操作的反操作去恢复
三、实现代码
#include <bits/stdc++.h>
using namespace std;
int depth; // 迭代加深的深度,也就是步数上限
int q[24]; // 变化中的棋盘
int path[1024]; // 操作的每一步动作,预估最多的操作是1024步
// 八个方向下标,共8行7列
int g[8][7] = {{0, 2, 6, 11, 15, 20, 22}, // A
{1, 3, 8, 12, 17, 21, 23}, // B
{10, 9, 8, 7, 6, 5, 4}, // C
{19, 18, 17, 16, 15, 14, 13}, // D
{23, 21, 17, 12, 8, 3, 1}, // E
{22, 20, 15, 11, 6, 2, 0}, // F
{13, 14, 15, 16, 17, 18, 19}, // G
{4, 5, 6, 7, 8, 9, 10}}; // H
// 中间八个位置格子号
int center[8] = {6, 7, 8, 11, 12, 15, 16, 17};
// 相反操作号
// 下标:当前的操作号,值:相反的操作号
int op[8] = {5, 4, 7, 6, 1, 0, 3, 2};
// 估价函数,统计中间八个格子里,出现次数最多的是多少次
// 估价函数的值,一定是小于等于真实的操作次数的
// 每次操作,最多能引入一个相同的数字,所以,如果现在有k个不同的
// 最少就需要8-k次操作才能保证将中间8个位置设置成全一样的数字
int f() {
// 函数内的数组,注意初始化,C++的特性是{0}表示所有数据为0,不是只第1个为0
// 用于计数1,2,3的数字个数
int b[4] = {0};
/*
center[i]:八个中间格子的标识
q[center[i]]:这八个中间格子在输入时的数字是什么
b[q[center[i]]]:计数,1,2,3这三个数字每个出现过几次
*/
int k = 0; // 出现最多的是几次,(不是哪个数字出现最多,是最多是几次)
for (int i = 0; i < 8; i++) b[q[center[i]]]++;
// 1,2,3 这三个数字,出现次数最多的是多少次?
for (int i = 1; i < 4; i++) k = max(k, b[i]);
// 估值:最少的操作次数
return 8 - k;
}
// 拽,x∈[0,7],共8种操作
void drag(int x) {
// g[x][0]:第几号
// q[g[x][0]]:这个号上现在是啥数字
// 每组7个数
int t = q[g[x][0]]; // 脑袋取出来
// 把中间6个依次上移
for (int i = 0; i < 6; i++) q[g[x][i]] = q[g[x][i + 1]];
// 把头上的数字放到尾巴上
q[g[x][6]] = t;
}
/*
Q:最小字典序怎么办?其实这是因为出题人不想写Special Judge来判断,只是想最终判断一下字符串是否一致,就是因为他懒,懂吧~
他懒,但是我们该怎么办呢?我们按啥顺序去搜索才能拿到最小字典序呢?
一般的情况,我们只要按字典序来搜索,就可以顺理成章的拿到最终的最小字典序~
就是每次在dfs搜索时,按从小到大的顺序来搜索就行啦
u :走几步了
pre :这一步,是由哪一步转化过来的,防止又走回去了
*/
bool dfs(int u, int pre) {
int t = f(); // 计算当前状态的预计最少拽的次数
if (u + t > depth) return false; // 如果已经拽过的次数+未来最少拽的次数大于约定的次数,那么此路不通
if (t == 0) return true; // 如果已经达到最终的目标,即f()=0,那么是成功完成
// 如果还没有完成目标,那么就枚举8个方向,从0-7,按字典序来枚举,看看这样拽行不行
for (int i = 0; i < 8; i++) {
// 如果在此状态前的一个动作pre是由i这个动作转化而来,那么不能再转回去
if (pre == op[i]) continue;
// 在此方向拽一下,使得地图变化
drag(i);
// 记录第u次操作的操作动作,比如A C D E等等
path[u] = i;
// 现在,本层我可以拽一下,那么这条路线是不是可以完成目标与我无关,与我的后继相关
if (dfs(u + 1, i)) return true;
// 恢复现场
drag(op[i]);
}
return false;
}
int main() {
while (scanf("%d", &q[0]) && q[0]) { // 判断输入是不是0的好办法
for (int i = 1; i < 24; i++) scanf("%d", &q[i]); // 第一个读取完了,其它的读取进来,共24个
// 可能不需要改变,中间8个本身就是一样的数字,最小移动步数为0
depth = 0;
// 迭代加深
while (!dfs(0, -1)) depth++;
// 如果最终最小移动步数为0,输出不需要移动
if (depth == 0)
puts("No moves needed");
else {
// 此题暗示我们,一定有解
// 输出字典序最小的解
for (int i = 0; i < depth; i++)
printf("%c", 'A' + path[i]);
puts("");
}
// 移动完成后,中间8个格子里的数字
// 中间那8个随便输入一个即可,内容都一样
printf("%d\n", q[6]);
}
return 0;
}
四、经验总结
#### 1、Q:A*可以做本题吗?A*怎么保证输出 字典序 ?
答:A*算法求字典序比较麻烦,因为 优先队列中 是 按估价函数排序 而非字典序排序,所以 除非将步数最小的所有方案全部求出,否则是无法求出字典序的。
本题用IDA*比较好。
2、顺序与复杂度
每步枚举 7 种操作(最优性剪枝,除去上一步的逆操作),若总步数为 k,则复杂度为 O(7^k)。玄学猜想,操作步数不会太多,但会出现 极深分支,因此可使用 迭代加深
3、最小字典序
每步按可选操作的 最小字典序枚举 可得到 最小字典序操作序列(相同层数,最小字典序最先搜到)
4、估价函数
每步会从中间移走一个数字,并移入一个数字,记中间最多数字的个数为 cnt,则至少需 8−cnt 步才能使中间全部变为同一数字,因此估价函数可定为 f(s)=8−cnt
5、坐标打表
对于方格较少的不规则图形,若可选操作的方式类似,仅目标方格不同,存储每种操作的目标方格映射能有效简化代码
6、总结
迭代加深 适用于答案层数 较浅,但某些分支特别深的问题,若估价函数容易找到,可搭配 A∗ 使用,此时变为 IDA∗,它能求出 最小步数 和 最小字典序操作序列