python

4.6 KiB

Raw Permalink Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

##AcWing 838. 堆排序

一、题目描述

输入一个长度为 n 的整数数列，从小到大输出前 m 小的数。

输入格式 第一行包含整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

输出格式 共一行，包含 m 个整数，表示整数数列中前 m 小的数。

数据范围 1≤m≤n≤10^5 ， 1≤数列中元素≤10^9

输入样例：

5 3
4 5 1 3 2

输出样例：

1 2 3

二、堆的数据结构

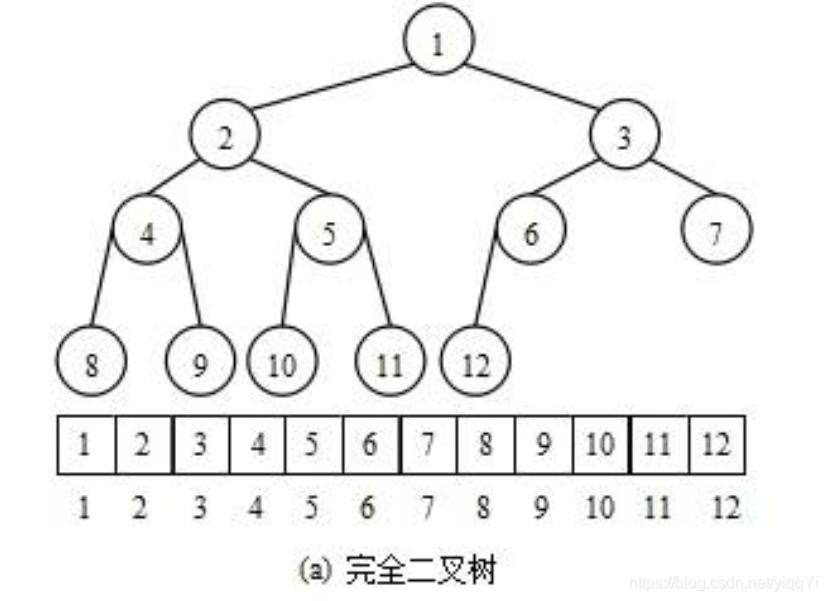
堆是一个完全二叉树:除了最后一层结点以外，上面的每一层都是满的。最后一层的结点是从左到右排布的。

小根堆：每一个点都是小于左右儿子的,所以根节点就是树中最小值.或者叫小顶堆。(递归定义)

存储方式：全新的存储方式，用一维数组来存。因为是完全二叉树，所有数据的下标是有规则可以找到的。

位置x, 左儿子2x , 右儿子2x+1

下标是从1开始的，从0开始不方便，因为2x还是自己没法玩。

三、堆操作的基本方法

down(x) 往下调整比如现在堆已经维护好了，我们要把头结点的值

	        1
            3       4	                               
          3   5   4   5

假设把头结点值换一下，换成6，

                   6
               3       4	                               
             3   5   4   5

现在就不是一个小顶堆了，因为6不比3，4小啊，所以需要对6进行调整，向下移动。

在3，4，6中找到一个最小值，然后交换3，6 （down操作时，如果当前结点大于左右儿子，与左右儿子中小的进行交换）

                3
           6         4	                               
        3     5   4     5

然后继续在6,3,5中找最小值，继续交换3,6

               3
           3        4	                               
        6    5   4     5

OK,移动完毕！

up(x) 往上调整比如现在堆已经维护好了，我们把5修改为2

          3
      3        4	                               
   3    5   4     2

就需要找出4,2 ，交换4,2 （与父结点对比，如果比父结点小，则交换自己与父结点）

        3
    3       2	                               
 3    5   4   4

继续查询3，2，发现在2<3,继续交换

         2
     3        3	                               
  3    5    4   4

不再交换，OK，移动完毕。

四、手写一个堆（小根堆）

1、插入一个数

    heap[++sz]=x; //在一维数组最后一个位置填充x
    up(sz);       //将最后一个元素不断上移

2、求最小值

    heap[1]

3、删除最小值

    heap[1]=heap[sz--]; //就是把尾部最后一个元素替换掉头元素，然后sz--
    down(1);            //然后再down(1)就行了

4、删除任意一个元素

    heap[k]=heap[sz--];
    down(k);
    up(k);   //其实只能执行一个，因为大了向下走。小了向上走嘛

5、修改任意一个元素

    heap[k]=x;
    down(k);
    up(k);

两个基本操作,这两个操作结合起来就能完成上面五个操作。 down(x) ---> 向下调整 up(x) ---> 向上调整

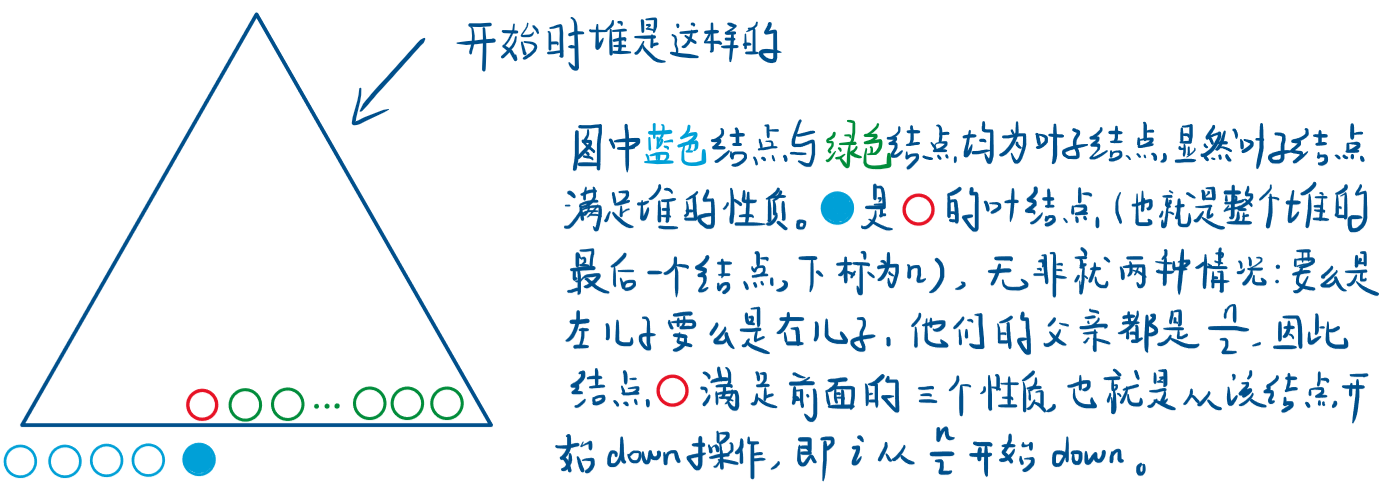
五、如何高效创建堆

六、完整代码

#include <bits/stdc++.h>

using namespace std;
const int N = 1e5 + 10;
int n, m;
int sz;
int heap[N];
void down(int u) {
    int t = u;
    if (u * 2 <= sz && heap[u * 2] < heap[t])t = u * 2;
    if (u * 2 + 1 <= sz && heap[u * 2 + 1] < heap[t])t = u * 2 + 1;
    if (u != t) {
        swap(heap[u], heap[t]);
        down(t);
    }
}
void up(int u) {
    while (u / 2 && heap[u / 2] > heap[u]) {
        swap(heap[u / 2], heap[u]);
        u /= 2;
    }
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> heap[i];

    sz = n;
    for (int i = n / 2; i >= 1; i--) down(i);

    while (m--) {
        printf("%d ", heap[1]);
        heap[1] = heap[sz--];
        down(1);
    }
    return 0;
}

4.6 KiB Raw Permalink Blame History Unescape Escape