python

6.0 KiB

Raw Permalink Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

poj 1830 开关问题题目传送门

1、描述

有一些开始状态的开关，题目让我们操控开关，使得开关从开始状态变成指定状态。

注意，当你操作一个开关，其关联的开关也会被操控。例如输入样例一，开始状态为000的三个开关，你要操作使其变成111。那么有以下四种方法：

只打开开关1，2 and 3和1关联，所以2 and 3也变成1
只打开开关2,3
只打开开关3,4
打开开关1,2,3

初始状态 0 0 0 0 终止状态 1 1 1 1 按下i号开关，会影响j号开关: 1 3 3 1 3 4 4 1 4 3 我能影响谁a_i a_1->(1,0,1,0)->{1,3}
a_2->(0,1,0,0)->{2}
a_3->{1,3,4}
a_4->{1,3,4}
谁能影响我k_i

操作每个开关后，影响的情况

2、问题解决

我们用线性方程组来求解。

\large [a_1,a_2,a_3] *  \begin{bmatrix}
 x_1 \\ 
 x_2 \\ 
 x_3 
\end{bmatrix} =b,即A_x=b

由上图表达式，我们可以思考，倘若乘号左边是开关的关联关系，乘号右边是开关操作，那么两个矩阵相乘，结果就是开关变化。由此，我们可以让b为开关变化。意思为当开关从0变为1，那么开关有变化，b_i为1；当开关无变化，则b_i为0。

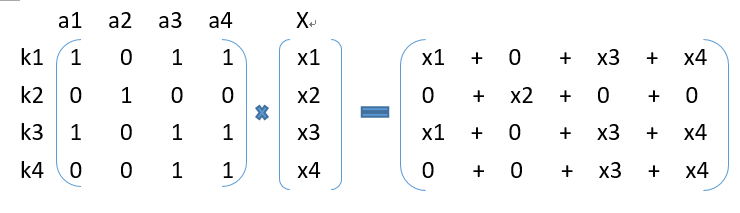
例如上面例子，a_1=(1,0,1,0)表示，操作开关1，开关3也会改变。即a[i][j]表示操作开关j，开关i也会变化。

所以，我们可以列出矩阵乘法表达式，然后进行高斯消元求解。

Q:为什么这里有反着记录的呢？ 答：我们希望以方程组的形式对原问题进行求解。那么，由于有n 盏灯，每个方程都要描述一盏灯的变化情况，这样的话，就共需要n个方程。我们以第1盏灯为例，我们知道它的初始状态和终止状态，我们就可以研究它是在初始状态下，通过什么样的操作变化到终止状态的。因为灯开关的特殊性，关联一次就变化一次，所以，我们还可以取一巧：看看开始状态和终止状态是一样的呢，还是有了变化。

一样的中间的变化是偶数次。用异或运算来描述就是异或和等于0。
不一样中间的变化是奇数次。用异或运算来描述就是异或和等1。

总结：我们关心的是状态的变化情况

1号灯的变化，受和它相关联灯的制约，以上面的图为例说明：第1盏灯的变化，受1,3,4三个灯的影响，我们可以把1盏灯的变化情况看作

\large 1*x_1+0*x_2+1*x_3+1*x_4

描述的说是:

1号灯操作，影响1号灯的状态
2号灯操作，不影响1号灯的状态
3号灯操作，影响1号灯的状态
4号灯操作，影响1号灯的状态

当然，只是说影响，但每个灯还有是权力决定自己是不是要操作的。这就引出了一个系数的问题： “我是一号灯，谁能影响我的状态？”

这玩意和题目中给的“我是x号灯，我能影响y号灯”是反着的，输入的时候要 小心识别 。

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;

const int N = 30;
const double eps = 10e-8;
int n;

int start[N]; //开始状态
int stop[N];  //结束状态

//高斯消元模板
double a[N][N]; //增广矩阵
int gauss() {
    int c, r; //当前列,行
    // 1、枚举系数每一列
    for (c = 0, r = 0; c < n; c++) {
        // 2、找出系数最大的行
        int t = r;
        for (int i = r; i < n; i++) //行
            if (abs(a[i][c]) > abs(a[t][c])) t = i;
        // 3、最大系数为0，直接下一列
        if (abs(a[t][c]) < eps) continue;
        // 4、交换
        if (r != t) // POJ中，如果二维数组，直接swap(a[t],a[r])会报编译错误，没办法，只好用了循环
            for (int i = 0; i < N; i++) swap(a[t][i], a[r][i]);
        // 5、倒序, 每项除a[r][c],化系数为1,处理的是方程左右两端，需要带着a[r][n]
        for (int i = n; i >= c; i--) a[r][i] /= a[r][c];
        // 6、用当前行将下面所有的列消成0
        for (int i = r + 1; i < n; i++)
            for (int j = n; j >= c; j--)
                a[i][j] -= a[r][j] * a[i][c];
        // 7、下一行
        r++;
    }

    if (r < n) {
        for (int i = r; i < n; i++)
            if (abs(a[i][n]) > eps)
                return -1; //无解
        return n - r;      //自由元个数
    }

    //倒三角，将已知解代入
    for (int i = n - 2; i >= 0; i--)
        for (int j = i + 1; j < n; j++)
            a[i][n] -= a[i][j] * a[j][n];

    //唯一解：0
    return 0;
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> n;
        memset(a, 0, sizeof(a));
        memset(start, 0, sizeof(start)); //初始化开始状态
        memset(stop, 0, sizeof(stop));   //初始化终止状态
        //输入起始状态(下标从0开始)
        for (int i = 0; i < n; i++) cin >> start[i];

        //输入终止状态(下标从0开始)
        for (int i = 0; i < n; i++) cin >> stop[i];

        //输入增广矩阵
        int x, y;
        while (cin >> x >> y && x != 0 && y != 0)
            a[y - 1][x - 1] = 1; //反着存入y-1受x-1影响

        for (int i = 0; i < n; i++) {
            a[i][n] = start[i] ^ stop[i]; //状态变化 start^stop
            a[i][i] = 1;                  //自己影响自己
        }

        //高斯消元模板
        int t = gauss();

        if (t == -1)
            cout << "Oh,it's impossible~!!" << endl;
        else
            cout << (1 << t) << endl;
    }
    return 0;
}

6.0 KiB Raw Permalink Blame History Unescape Escape

1、描述

2、问题解决

6.0 KiB

Raw Permalink Blame History Unescape Escape