python

3.5 KiB

Raw Permalink Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

##AcWing 893. 集合-Nim游戏

一、题目描述

给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 S，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式 第一行包含整数 k，表示数字集合 S 中数字的个数。

第二行包含 k 个整数，其中第 i 个整数表示数字集合 S 中的第 i 个数 s_i。

第三行包含整数 n。

第四行包含 n 个整数，其中第 i 个整数表示第 i 堆石子的数量 h_i。

输出格式 如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围 1≤n,k≤100,1≤s_i,h_i≤10000

输入样例：

输出样例：

Yes

二、理论知识

理解题意：集合S中有两个数(k=2),分别是2和5。也就是拿一次不是任意个，是必须2或5个。有3堆石子，个数分别是2,4,7。问我们是先手必胜还是先手必败。

mex函数

对于集合S,mex(S)=mex(\{x_1,x_2…\})表示S中没有出现的最小非负整数。

例如:S=\{0,1,2,4\},那么mex(S)=3。
sg函数 sg(n)=mex(\{sg(i_1),sg(i_2),sg(i_3)...\})。 n为结点；i_1,i_2,i_3…是n的后继结点。
规定 sg(G)=sg(head)。 G是一个有向图,head是G的头结点。
结论 sg(G1) ^ sg(G2) ^ sg(G3) ^ … ^ sg(Gn)为n个有向图的异或和,对于n个有向图游戏,这个异或和就是它的答案。

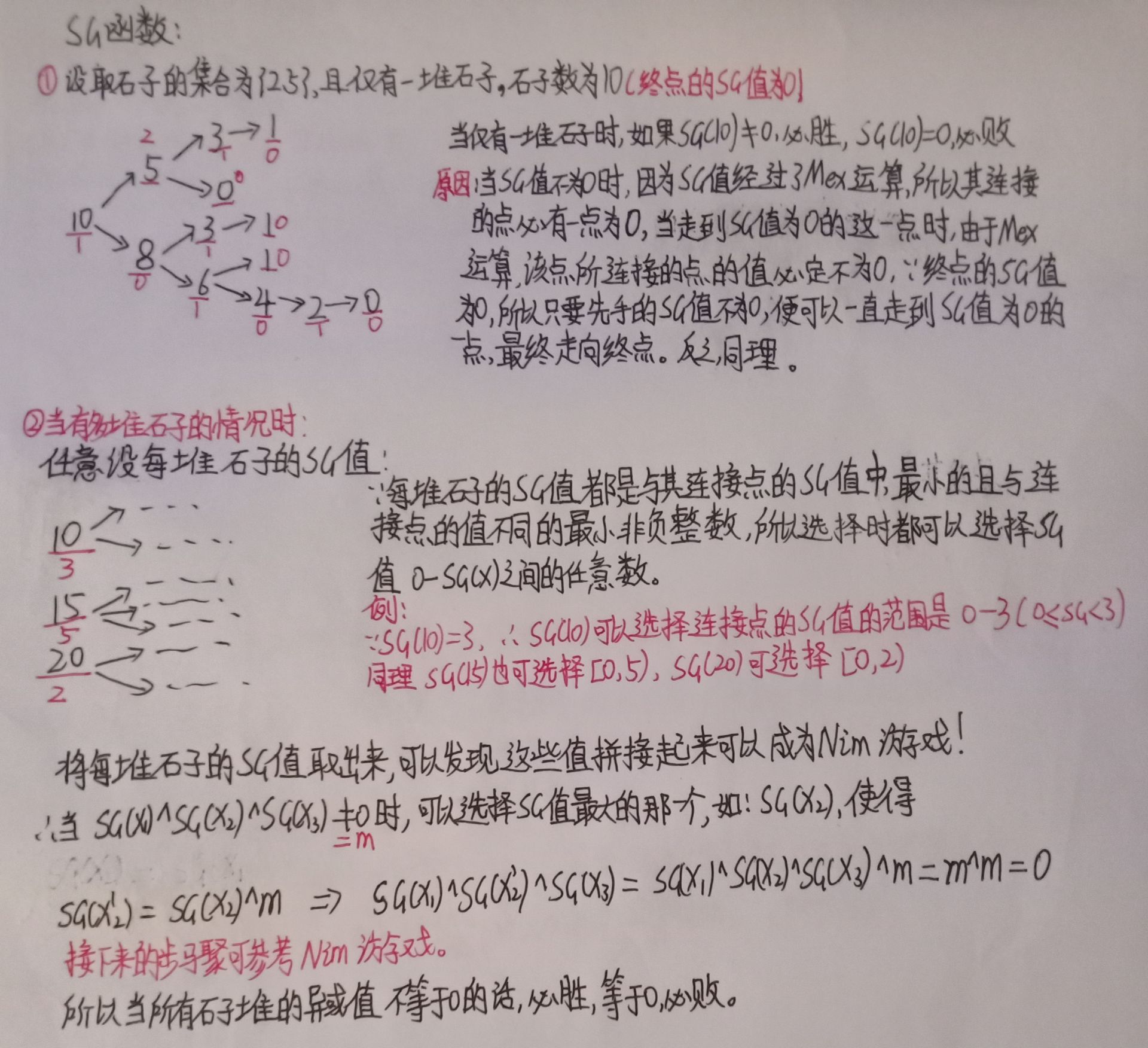
三、实例解析

SG函数是解决博弈论问题的一把利器。

四、`SG`函数复用的原因

五、实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 110;
const int M = 10010;

int n, k;
int a[N]; // 一共几种取法，比如一次取2个或5个。
int f[M]; // SG函数的值
int res;

int sg(int x) {
    if (~f[x]) return f[x]; // 记忆化搜索

    unordered_set<int> S;
    for (int i = 0; i < k; i++)
        if (x >= a[i]) S.insert(sg(x - a[i])); // x-s[i]:x的可行路径中终点有哪几个; sg(x-s[i]):这个终点它的sg值

    for (int i = 0;; i++)
        if (!S.count(i)) return f[x] = i;
}

int main() {
    memset(f, -1, sizeof f); // 初始化数组值为-1
    cin >> k;                // 表示数字集合S中数字的个数
    for (int i = 0; i < k; i++) cin >> a[i];

    cin >> n; // 一共几堆
    // n堆石子，每堆石子都取SG值，然后异或在一起
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x; // 每堆里多少个
        res ^= sg(x);
    }
    if (res)
        puts("Yes"); // 如果不是零，必胜
    else
        puts("No"); // 如果是零，必败

    return 0;
}

3.5 KiB Raw Permalink Blame History Unescape Escape