|
|
## $AcWing$ $205$. 斐波那契
|
|
|
|
|
|
[题目传送门](https://www.luogu.com.cn/problem/P1962)
|
|
|
|
|
|
### 一、题目描述
|
|
|
在斐波那契数列中,$F_ib_0=0,F_ib_1=1,F_ib_n=F_ib_{n−1}+F_ib_{n−2}(n>1)$。
|
|
|
|
|
|
给定整数 $n$,求 $F_ib_n~ mod ~ 10000$。
|
|
|
|
|
|
**输入格式**
|
|
|
输入包含多组测试用例。
|
|
|
|
|
|
每个测试用例占一行,包含一个整数 $n$。
|
|
|
|
|
|
当输入用例 $n=−1$ 时,表示输入终止,且该用例无需处理。
|
|
|
|
|
|
**输出格式**
|
|
|
每个测试用例输出一个整数表示结果。
|
|
|
|
|
|
每个结果占一行。
|
|
|
|
|
|
**数据范围**
|
|
|
$0≤n≤2×10^9$
|
|
|
|
|
|
### 二、矩阵乘法
|
|
|
|
|
|
设 $A$ 为 $P \times M$的矩阵,$B$ 为 $M \times Q$ 的矩阵,设矩阵 $C$ 为矩阵 $A$ 与 $B$ 的乘积,
|
|
|
|
|
|
其中矩阵 $C$ 中的第 $i$ 行第 $j$ 列元素可以表示为:
|
|
|
|
|
|
$$\large C_{i,j} = \sum_{k=1}^MA_{i,k}B_{k,j}$$
|
|
|
|
|
|
如果没看懂上面的式子,没关系。通俗的讲,在矩阵乘法中,结果 $C$ 矩阵的第 $i$ 行第 $j$ 列的数,就是由矩阵 $A$ 第 $i$ 行 $M$ 个数与矩阵 $B$ 第 $j$ 列 $M$ 个数分别 **①相乘** 再 **②相加** 得到的。
|
|
|
|
|
|
> 相关性质
|
|
|
乘法结合律:$(AB)C=A(BC)(AB)C=A(BC)$
|
|
|
单位矩阵:$AE=EA=A$,其中的单位矩阵 $E$ 符合:行数等于列数,对角线上的元素都是 $1$,其余都是 $0$
|
|
|
|
|
|
### 三、本题题解
|
|
|
|
|
|
如果有一道题目让你求斐波那契数列第 $n$ 项的值,**最简单的方法** 莫过于直接 **递推**。但是如果 $n$ 的范围达到了 $10^{9}$级别,递推就不行了,稳稳 $TLE$, 考虑 **矩阵加速递推**:
|
|
|
|
|
|
|
|
|
斐波那契数列($Fibonacci$ $Sequence$)大家应该都非常的熟悉了。在斐波那契数列当中,
|
|
|
|
|
|
我们知道,斐波那契数列有这样的定义:
|
|
|
|
|
|
$$\large f_i = f_{i−1}+f_{i−2}$$
|
|
|
|
|
|
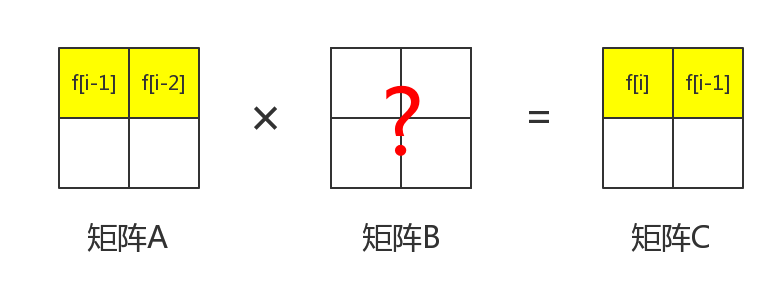
那么如果我们有一个$2 × 2 $的矩阵,其中第一行分别是$f_{i − 1}$ 和$f_{i-2}$。我们的目标是把第一行乘上一个矩阵变成$f_i$和$f_{i-1}$。那么应该怎么办呢?
|
|
|
|
|
|
|
|
|
首先,矩阵$A$和矩阵$C$都含有$f_{i-1}$ 这一项。那么就先从这里下手。
|
|
|
我们知道,矩阵$C$的$f_{i-1}$在第$1$行第$2$列。那么,根据公式,可以得到
|
|
|
$$\large C_{1 , 2} = A_{ 1 , 1} × B_{1,2} + A_{1 , 2} × B_{ 2 , 2}$$
|
|
|
|
|
|
也就是说
|
|
|
$$\large f_{i-1}=f_{i-1}\times B_{1,2} +f_{i-2}\times B_{2,2}$$
|
|
|
|
|
|
|
|
|
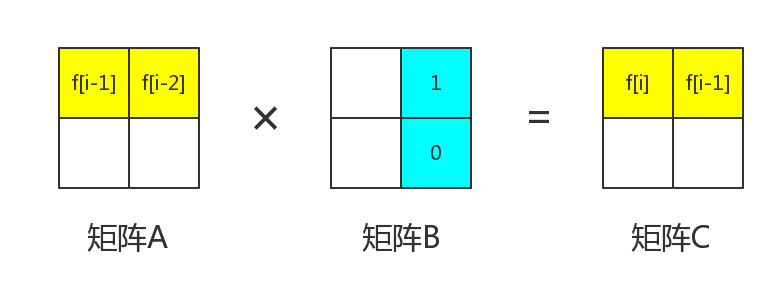
那么很明显,我们可以得到$B_{1,2}=1,B_{2,2}=0$。这样可以保证进行矩阵乘法之后$C_{1,2}$ 是$f_{i-1}$。
|
|
|
|
|
|
|
|
|
那么现在来看矩阵$C$中的$f_i$。我们要保证的是
|
|
|
$$\large C_{1,1} =A_{1,1} ×B_{1,1} +A_{1,2} ×B_{2,1}$$
|
|
|
|
|
|
也就是说
|
|
|
$$\large f_{i}=f_{i-1}\times B_{1,1}+f_{i-2}\times B_{2,1}$$
|
|
|
|
|
|
|
|
|
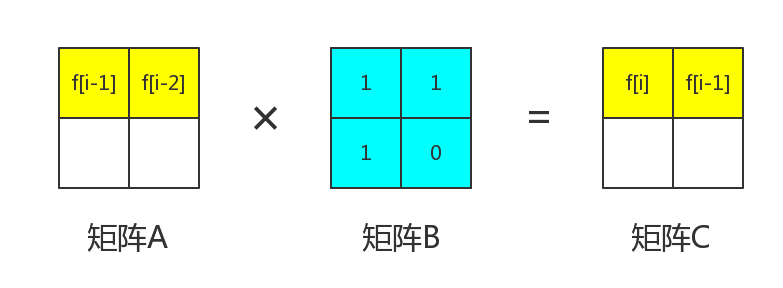
我们知道,$f_i=f_{i-1}+f_{i-2}$。所以可以得到$B_{1,1}=1,B_{2,1}=1$
|
|
|
|
|
|
|
|
|
那么整个矩阵$B$都被我们求出来了。
|
|
|
得到了$f_i$ 和$f_{i-1}$ 后,我们再将它乘一次矩阵$B$,就可以得到$f_{i+1}$和$f_i$,又可以得到$f_{i+2}$和$f_{i+1}...$,这样就可以得到$f_n$了。
|
|
|
|
|
|
**但是!**
|
|
|
你以为就结束了?
|
|
|
这样的时间复杂度是$O(nm^2)$,其中$n$表示求斐波那契数列的第$n$项,$m$表示矩阵的长宽,还不如递推。而且递推可以得到$1$到$n$的所有斐波那契数,而矩阵乘法只能求第$n项。
|
|
|
|
|
|
其实还有个地方可以优化。
|
|
|
我们求$f_n$的时候其实是将原矩阵$A$乘了$n − 1$次矩阵$B$的。也就是说
|
|
|
$$\large 目标矩阵=A×B^{n−1}$$
|
|
|
|
|
|
看到$n − 1$次方想到了什么?
|
|
|
可以用 **快速幂**!
|
|
|
我们用快速幂的思想求出$B^{n-1}$,然后再乘上一个矩阵$A$即可。
|
|
|
|
|
|
怎么用快速幂?
|
|
|
其实是一个道理。只不过把矩阵$A$乘矩阵$B$换成矩阵$B$乘矩阵$B$就可以了。
|
|
|
那么最终的时间复杂度为$O(m^3logn)$。还是很优秀的。
|
|
|
|
|
|
|
|
|
<font color='red' size=4><b>注意</b></font>
|
|
|
矩阵乘法不满足交换律,所以一定不能写成 $\left[\begin{array}{ccc} 1 & 1 \\ 1 & 0 \end{array}\right]^{n-2} \times \left[\begin{array}{ccc}1 & 1\end{array}\right]$ 的第一行第一列元素。
|
|
|
|
|
|
* 对于 $n \leq 2$ 的情况,直接输出 $1$ 即可,不需要执行矩阵快速幂。
|
|
|
|
|
|
* 为什么要乘上 $base$ 矩阵的 $n-2$ 次方而不是 $n$ 次方呢?因为 $F_1, F_2$ 是不需要进行矩阵乘法就能求的。也就是说,如果只进行一次乘法,就已经求出 $F_3$了。如果还不是很理解为什么幂是 $n-2$,建议手算一下。
|
|
|
|
|
|
### 四、实现代码
|
|
|
```c++
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
const int N = 10; //这个黄海实测,写成3也可以AC,考虑到矩阵乘法的维度,一般写成10,差不多的都可以过掉
|
|
|
const int MOD = 10000;
|
|
|
|
|
|
int base[N][N], res[N][N];
|
|
|
int t[N][N];
|
|
|
|
|
|
//矩阵乘法,为快速幂提供支撑
|
|
|
inline void mul(int C[][N], int A[][N], int B[][N]) {
|
|
|
memset(t, 0, sizeof t);
|
|
|
for (int k = 1; k <= 2; k++)
|
|
|
for (int i = 1; i <= 2; i++)
|
|
|
for (int j = 1; j <= 2; j++)
|
|
|
t[i][j] = (t[i][j] + (A[i][k] * B[k][j]) % MOD) % MOD;
|
|
|
memcpy(C, t, sizeof t);
|
|
|
}
|
|
|
|
|
|
//快速幂
|
|
|
void qmi(int k) {
|
|
|
memset(res, 0, sizeof res);
|
|
|
res[1][1] = res[1][2] = 1; //结果是一个横着走,一行两列的矩阵
|
|
|
// P * M 与 M * Q 的矩阵才能做矩阵乘积,背下来即可
|
|
|
//矩阵快速幂,就是乘k次 base矩阵,将结果保存到res中
|
|
|
//本质上就是利用二进制+log_2N的特点进行优化
|
|
|
while (k) {
|
|
|
//比如 1101
|
|
|
if (k & 1) mul(res, res, base); // res=res*b
|
|
|
mul(base, base, base); //上一轮的翻番base*=base
|
|
|
k >>= 1; //不断右移
|
|
|
}
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
int n;
|
|
|
while (cin >> n) {
|
|
|
if (n == -1) break;
|
|
|
if (n == 0) {
|
|
|
puts("0");
|
|
|
continue;
|
|
|
}
|
|
|
if (n <= 2) {
|
|
|
puts("1");
|
|
|
continue;
|
|
|
}
|
|
|
|
|
|
// base矩阵
|
|
|
memset(base, 0, sizeof base);
|
|
|
/**
|
|
|
1 1
|
|
|
1 0
|
|
|
|
|
|
第一行第一列为1
|
|
|
第一行第二列为1
|
|
|
第二行第一列为1
|
|
|
第二行第二列为0 不需要设置,默认值
|
|
|
*/
|
|
|
base[1][1] = base[1][2] = base[2][1] = 1;
|
|
|
|
|
|
//快速幂
|
|
|
qmi(n - 2);
|
|
|
|
|
|
//结果
|
|
|
printf("%d\n", res[1][1]);
|
|
|
}
|
|
|
|
|
|
return 0;
|
|
|
}
|
|
|
|
|
|
```
|
|
|
### 五、思考题
|
|
|
https://blog.csdn.net/weixin_42638946/article/details/115872469
|
|
|
|
|
|
使用 **快速幂优化** 计算以下数列第 $n$ 项 $mod ~10^9+7$ 的值:
|
|
|
|
|
|
1. $\large a_n=a_{n−1}+2a_{n−2}~(a_1=0,a_2=1)$
|
|
|
|
|
|
**解**:$\large F_n=F_{n-1}+2F_{n-2}$
|
|
|
|
|
|
$\large G(n)=[F_{n},F_{n-1}],G(n-1)=[F_{n-1},F_{n-2}]$
|
|
|
|
|
|
思考 $G(n-1)$ 如何变化可以到达 $G(n)$ ?
|
|
|
$$\large G(n)=G(n-1) \times \left[\begin{array}{ccc} 1 & 1 \\ 2 & 0 \end{array}\right] \\
|
|
|
\Rightarrow \\
|
|
|
\large [F_{n},F_{n-1}]=[F_{n-1},F_{n-2}] \times \left[\begin{array}{ccc} 1 & 1 \\ 2 & 0 \end{array}\right] \\
|
|
|
\Rightarrow $$
|
|
|
|
|
|
$$\large =[F_{2},F_{1}] \times \left[\begin{array}{ccc} 1 & 1 \\ 2 & 0 \end{array}\right]^{n-1}=[1,0] \times \left[\begin{array}{ccc} 1 & 1 \\ 2 & 0 \end{array}\right]^{n-1}$$
|
|
|
|
|
|
|
|
|
---
|
|
|
|
|
|
2. $\large a_n=3a_{n−1}−2a_{n−2}+1 ~(a_1=0,a_2=1)$
|
|
|
|
|
|
3. $\large \displaystyle a_n=\sum_{i=1}^{n−1}[(n−i)×a_i]~(a_1=1)$
|
|
|
|
|
|
4. $\large a_n=a_{n−1}×a_{n−2}~(a_1=2,a_2=3)$
|
|
|
|
|
|
矩阵快速幂的一些题目
|
|
|
https://blog.csdn.net/ypeij/article/details/118785530
|
|
|
|
|
|
矩阵快速幂
|
|
|
https://www.cnblogs.com/mk-oi/p/13591627.html |