4.3 KiB
### 一、从普通前缀和引入
-
普通前缀和 采用
s_n=a_1+a_2+...+a_n,计算普通前缀和。 -
动态前缀和 如果在求前缀和的过程中,某个
a_i修改了,那么原来统计好的s_i就不对了,而且可能修改的还不只一个,这样,普通前缀和就不好用了,此时,可以用树状数组来解决。
二、树状数组基础

如上图:
c[1]管理a[1];
c[2]管理c[1],a[2];
c[3]管理a[3];
c[4]管理c[2],c[3],a[4];
c[i]管辖区间范围规定

总结:i管辖的区间长度,要看i的二进制表示法最后有几个0,比如有k个0,它管辖的个数就是2^k个。
\large 管辖范围: (a[i]-2^k+1) \sim a[i]
举个栗子:i=(4)_{10}=(0100)_2,二进制表示法最后两位是0,所以它的管理范围是2^2=4,即a[1]\sim a[4]。
再来一个,i=(8)_{10}=(1000)_2,二进制表示法最后三位是0,所以它的管理范围是2^3=8,即a[1]\sim a[8]。
c[i]管辖区间范围计算办法

如上图,我们想要得i=20的最后面的几个0,也就是求最后面的100(红色椭圆里面的数字),可以通过二进制运算的lowbit运算就可以得到。
总结:lowbit函数可以取得原数二进制表示法中最后一个1。
\large c[i]区间长度计算办法:lowbit(i)=(-i)\&i前驱与后继
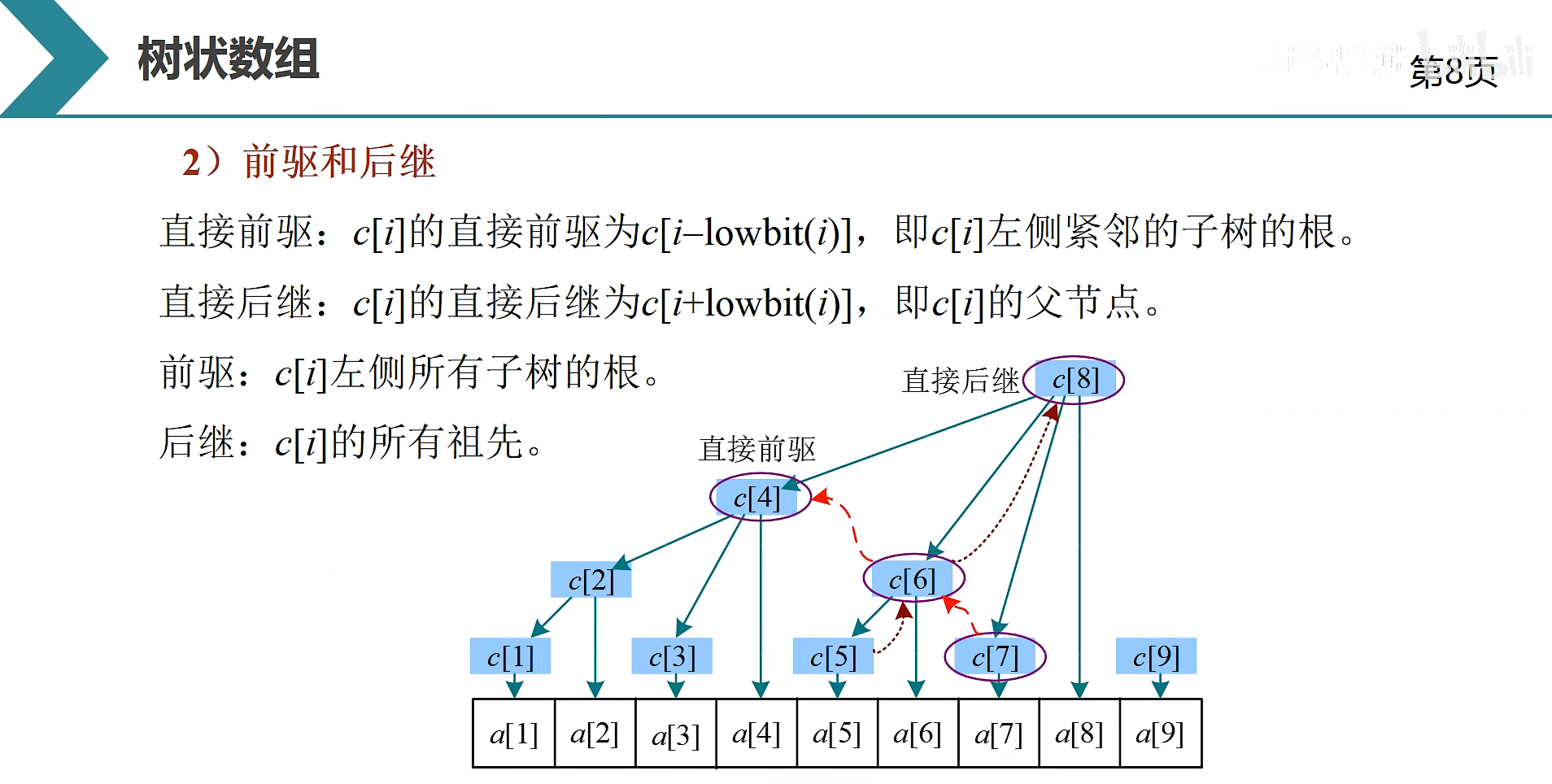
直接前驱
\large c[i-lowbit(i)]直接后继
\large c[i+lowbit(i)]树状数组下标从1开始,不能从0开始。因为数组长度是lowbit(i),如果从0开始,lowbit(0)=(-i)\&i=0,那么前驱就是c[0-0]=c[0],就一直不变,死循环。
小结:树状数组下标从1开始。
如果我们现在将树状数组记录的是a[i]的前缀和数组,那么$sum[7]=c[7]+c[6]+c[4]$
这是因为c[7]管着a[7],c[6]管着a[5],a[6],c[4]管着a[1],a[2],a[3],a[4]。
小结:查询找所有前驱,更新改所有后继。
树状数组操作
- 点更新
- 查询前缀
两者都是
O(logn)的时间复杂度。 假设n=1e9,则此时操作次数就是log10^9=30,速度极快。
三、实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, a[N];
//下面是用树状数组完成前缀和的保存办法
#define lowbit(x) (x & -x)
int c[N];
//点更新
void add(int i, int z) {
for (; i <= n; i += lowbit(i)) c[i] += z; //更新所有祖先
}
//前缀和
int sum(int i) {
int s = 0;
for (; i; i = i - lowbit(i)) s += c[i];
return s;
}
//区间和
int sum(int i, int j) {
return sum(j) - sum(i - 1);
}
/*
测试用例:
5
2 3 1 4 5
*/
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
add(i, a[i]);
}
//利用树状数组求前缀和
printf("%d\n", sum(4));
//利用树状数组求区间和
printf("%d\n", sum(5) - sum(3));
return 0;
}
四、树状数组应用
#### 1、树状数组求区间最大值 https://blog.csdn.net/weixin_46048848/article/details/108529488


