python

6.9 KiB

Raw Permalink Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

`AcWing` `175`. 电路维修

一、题目描述

达达是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女翰翰，从而被收留在地球上。

翰翰的家里有一辆飞行车。

有一天飞行车的电路板突然出现了故障，导致无法启动。

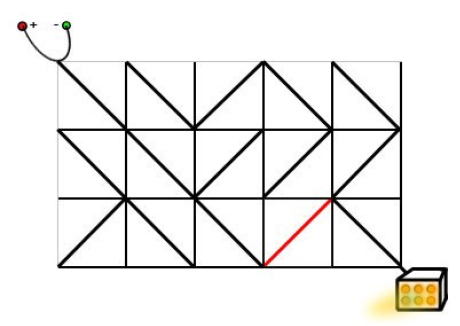
电路板的整体结构是一个 R 行 C 列的网格（R,C≤500），如下图所示。

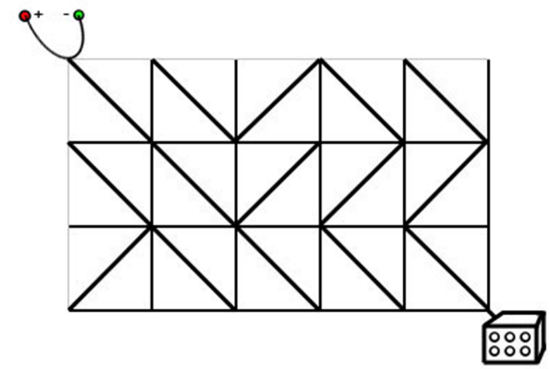
每个格点都是电线的接点，每个格子都包含一个电子元件。

电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。

在旋转之后，它就可以连接另一条对角线的两个接点。

电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

达达发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。

她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。

不过，电路的规模实在是太大了，达达并不擅长编程，希望你能够帮她解决这个问题。

注意：只能走斜向的线段，水平和竖直线段不能走。

输入格式 输入文件包含多组测试数据。

第一行包含一个整数 T，表示测试数据的数目。

对于每组测试数据，第一行包含正整数 R 和 C，表示电路板的行数和列数。

之后 R 行，每行 C 个字符，字符是"/"和""中的一个，表示标准件的方向。

输出格式 对于每组测试数据，在单独的一行输出一个正整数，表示所需的最小旋转次数。

如果无论怎样都不能使得电源和发动机之间连通，输出 NO SOLUTION。

数据范围 1≤R,C≤500,1≤T≤5

输入样例：

1
3 5
\\/\\
\\///
/\\\\

输出样例：

样例解释 样例的输入对应于题目描述中的情况。

只需要按照下面的方式旋转标准件，就可以使得电源和发动机之间连通。

二、算法分析

双端队列主要解决图中边的权值只有 0 或者 1 的 最短路问题

左上角起始点坐标(0,0),右下角终点坐标(n,m),现在想从左上角走到右下角。
把电路板上每一个格子点(交叉点)看作无向图中的节点,认为两个节点x和y是某个小方格的两个对角:
如果x和y的线段\,那么边权为0（可以直接走，不用掰）
如果x和y线段是/,那么边权为1（不能直接走，需要掰）

操作每次从队头取出元素，拓展其它元素时

若拓展某一元素的边权是 0，则将该元素插入到队头
若拓展某一元素的边权是 1，则将该元素插入到队尾

`Q1:`为啥要这么干？

答：要保证最短路径，最先找到

解释一下：

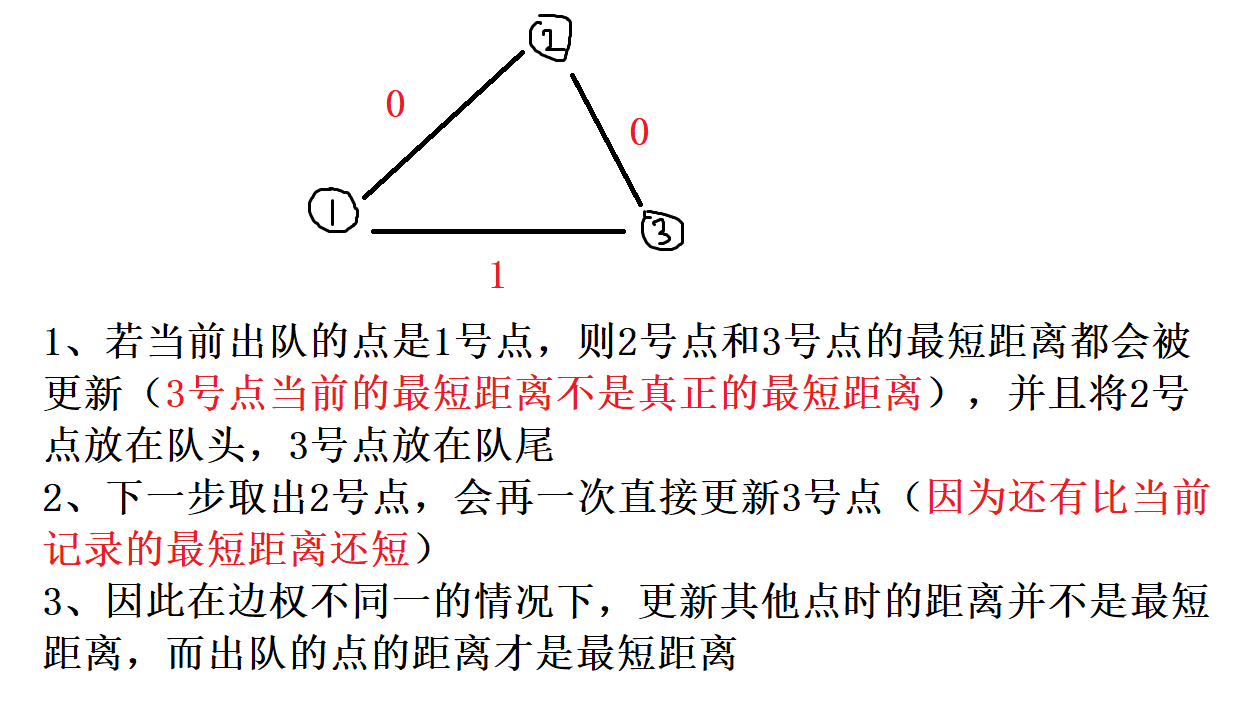
与 堆优化 Dijkstra 一样，必须在 出队时 才知道 每个点最终的最小值 ，原因如下:

`Q2:`格子和点怎么标记？

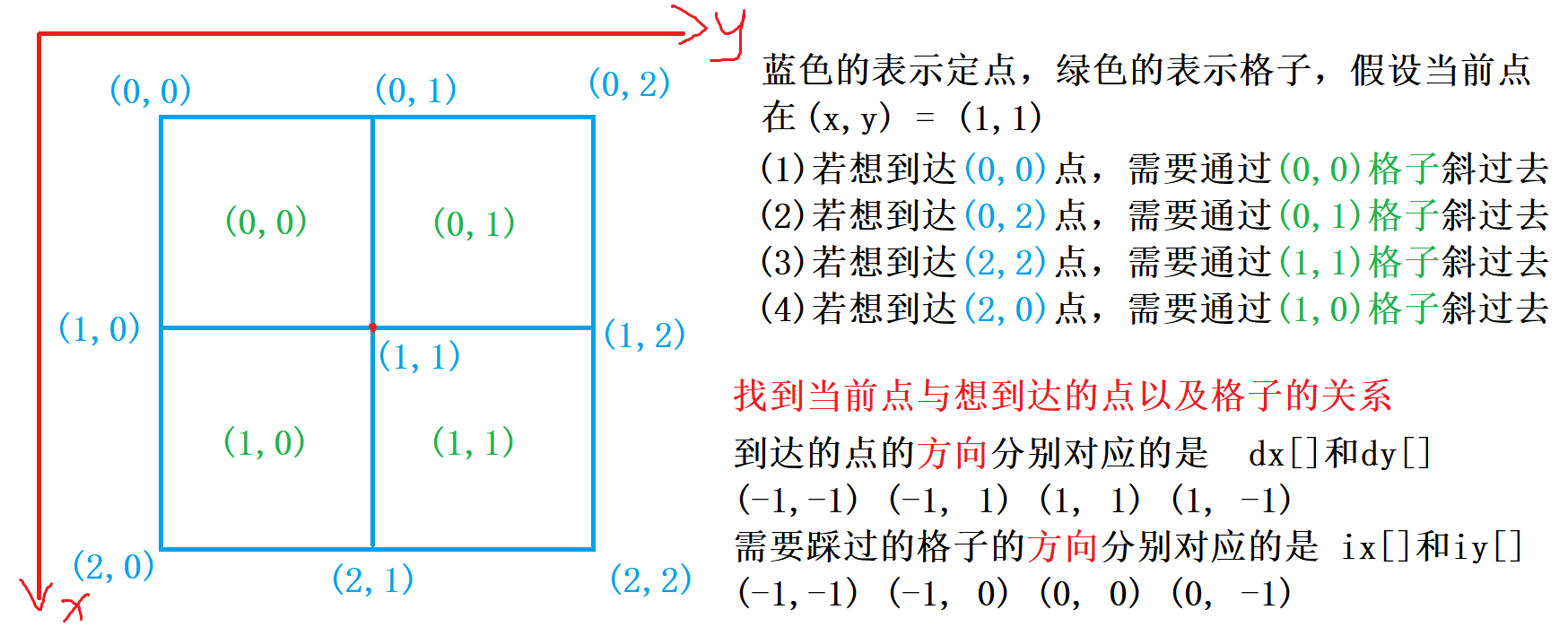
图中的格子和点是不一样的，点是格子上的角角上的点，每个点都有4个方向可以走，分别对应的是 左上角， 右上角 ，右下角 ，左下角

踩过格子 到达想去的点时，需要判断是否需要 旋转电线，若旋转电线表示从 当前点 到 想去的点 的边权是 1 ，若不旋转电线则边权是 0。

按 左上角 ，右上角 ，右下角 ，左下角 遍历的顺序

1、dx[]和dy[] 表示某点可以去 其它点 的方向

2、ix[]和iy[]表示需要踩某个方向的格子才能去到 相应的点

3、cs[]表示当前点走到4个方向的点理想状态下格子形状(边权是0)

左上：\
右上: /
右下：\
左下：/

如果不是这样的情况，就说明需要调整，边权就是1

代码中dx,dy、ix,iy、连通字符cs[] 是按照左上右上右下左下来构造的,三者必须按照统一的方向构造

三、双端队列

280 ms 性能优秀

#include <bits/stdc++.h>

using namespace std;
const int INF = 0x3f3f3f3f;

typedef pair<int, int> PII;
#define x first
#define y second

const int N = 510;
int n, m;     // n行m列
char g[N][N]; // 地图

int dist[N][N]; // 距离出发点的距离

// 左上，右上，右下，左下
// 如果与cs[i]的字符相匹配，表示现在就是你想要的路线，不需要花钱，否则交1元钱
char cs[] = "\\/\\/";
// 点的四个偏移量
int dx[] = {-1, -1, 1, 1};
int dy[] = {-1, 1, 1, -1};
// 踩格子的偏移量
int ix[] = {-1, -1, 0, 0};
int iy[] = {-1, 0, 0, -1};

deque<PII> q; // 双端队列主要解决图中边的权值只有0或者1的最短路问题
void bfs() {
    // 多组数据，清空
    q.clear();
    memset(dist, 0x3f, sizeof dist);

    // 将{0,0}入队列，第一个要搜索的位置
    dist[0][0] = 0;
    q.push_back({0, 0});

    while (q.size()) {
        PII t = q.front();
        q.pop_front();

        for (int i = 0; i < 4; i++) {
            int x = t.x + dx[i], y = t.y + dy[i];
            if (x < 0 || x > n || y < 0 || y > m) continue; // 出界

            // 走向这个点需要经过哪个格子
            int a = t.x + ix[i], b = t.y + iy[i];

            // 通过是否匹配计算权值是0，还是1，修改距离
            int d = dist[t.x][t.y] + (g[a][b] != cs[i]);

            // 发现更小值
            if (d < dist[x][y]) {
                dist[x][y] = d; // 更新更小值
                // 权值为1，加队尾
                // 权值为0，加队头
                g[a][b] == cs[i] ? q.push_front({x, y}) : q.push_back({x, y});
            }
        }
    }
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> n >> m;

        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                cin >> g[i][j];

        // 双端队列宽搜
        bfs();

        // 如果无法取得最短路
        if (dist[n][m] == INF)
            puts("NO SOLUTION");
        else
            printf("%d\n", dist[n][m]);
    }
    return 0;
}

6.9 KiB Raw Permalink Blame History Unescape Escape

AcWing 175. 电路维修