13 KiB
【学习笔记】动态规划—斜率优化DP
https://www.jianshu.com/p/72387491a758 https://blog.csdn.net/tanjunming2020/article/details/126977257
【前言】
第一次写这么长的文章。
写完后对 斜优 的理解又加深了不少(update 2020.6.19: 回过头来看这句话满是讽刺啊,明明这时候连 基本的概念 都 没有理清 ....)。
本文讲解较详,只要耐心读下去,相信大部分 OIer 都能看懂。
斜率优化 dp,顾名思义就是利用 斜率相关性质 对 dp 进行优化。
斜率优化 通常可以 由两种方式来理解 ,需要灵活地运用数学上的 数形结合, 线性规划 思想。
按照正常思路列出DP方程后,如发现其形如\large dp[i]=Min/Max(dp[j]+v[j]\times w[i])的形式,即可使用斜率优化DP。(v[j]和w[i]分别表示两个关于j和i的函数)
该方程的关键点在于 v[j] \times w[i] 这一项,它既有 i 又有 j,于是 单调队列优化 不再适用,可以 尝试 使用 斜率优化。
一.【理解方式】
以 【模板】 玩具装箱 toy [P3195] 为例,两种斜优的理解方式。
设 \large \displaystyle S[n]=\sum_{i=1}^n(C[i]+1),用 dp[i] 表示装好前 i 个的最小花费,则转移方程为:
\large dp[i]=min(dp[j]+(S[i]−S[j]−1−L)^2)注:两件玩具之间要加入一个单位长度的填充物,j+1 \sim i的话,最后一个i里没有这个一个单位长度,需要减去1。
为方便描述,将 L 提前加 1,再把 min 去掉,得到状态转移方程:
\large dp[i]=dp[j]+(S[i]−S[j]−L)^2化简得:
\large dp[i]=S[i]^2−2S[i]L+dp[j]+(S[j]+L)^2−2S[i]S[j]1.【代数法(数形结合)】
只含 L 的项对于每一个 i 的 择优筛选 过程都是完全一样的值,只含 Function(i) 的项在一次 i 的择优筛选过程中不变,含 Function(j) 的项可能会不断变化(在本题中表现为为严格单增)。
我们以此为划分依据,把同类型的项用括号括起来,即:
\large dp[i]=(−2S[i]S[j])+(dp[j]+(S[j]+L)^2)+(S[i]^2−2S[i]L)(1).【维护一个凸包】
设 j_1,j_2 (0⩽j_1<j_2<i) 为 i 的两个决策点,且满足决策点 j_2 优于 j_1,
有: \large (−2S[i]S[j_2])+(dp[j_2]+(S[j_2]+L)^2)+(S[i]^2−2S[i]L)⩽(−2S[i]S[j_1])+(dp[j_1]+(S[j_1]+L)^2)+(S[i]^2−2S[i]L) \
\Rightarrow \
\large (−2S[i]S[j_2])+(dp[j_2]+(S[j_2]+L)^2)⩽(−2S[i]S[j_1])+(dp[j_1]+(S[j_1]+L)^2)
划重点:此处移项需要遵循的原则是:参变分离。将 Function(i) 视作未知量,用 Function(j) 来表示出 Function(i) 。
移项得:\large −2S[i](S[j_2]−S[j_1])⩽(dp[j_1]+(S[j_1]+L)^2)−(dp[j_2]+(S[j_2]+L)^2)
∵C[j]⩾1
∴S[j+1]>S[j]
又∵j_2>j_1
∴S[j2]−S[j1]>0
\large ∴2S[i]⩾ \frac{(dp[j_2]+(S[j_2]+L)^2)−(dp[j_1]+(S[j_1]+L)^2)}{S[j_2]−S[j_1]}
设 Y(j)=dp[j]+(S[j]+L)^2,X(j)=S[j]
即\large 2S[i]⩾ \frac{Y(j_2)−Y(j_1)}{X(j_2)−X(j_1)}
显然等式右边是一个关于点 P(j_2) 和 P(j_1) 的斜率式,其中
P(j)=(X(j),Y(j))=(S[j],dp[j]+(S[j]+L)^2)
也就是说,如果存在两个决策点 j_1,j_2 满足 (0⩽j_1<j_2<i),使得不等式
\large \frac{Y(j_2)−Y(j_1)}{X(j_2)−X(j_1)}⩽2S[i]划重点:斜优灵活多变,细节麻烦也多,所以尽量将问题模式化。 比如这里的最终公式,尽量化为
\frac{Y(j)−Y(j′)}{X(j)−X(j′)}的形式,而不是\frac{(Y(j))−Y(j′)}{X(j′)−X(j)},虽然直接做一般也不会出什么问题,但这样子可以方便理解,方便判断凸包方向等等。
假设有酱紫的三个点 P(j_1),P(j_2),P(j_3),k_1,k_2 为斜率,如下图所示情况(三点分别为 A,B,C):
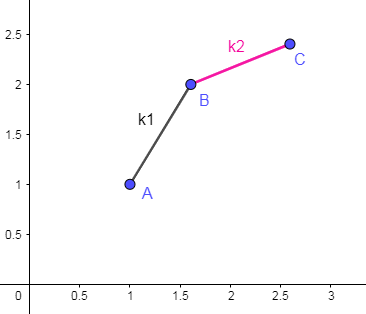
显然有 k_2<k_1。设 k_0=2S[i],由上述结论可知:
(
a). 若k_1⩽k_0,则j_2优于j_1。反之,若k_1>k_0,则j_1优于j_2。 (b). 若k_2⩽k_0,则j_3优于j_2。反之,若k_2>k_0,则j_2优于j_3。
于是这里可以分三种情况来讨论:
(1).
k_0<k_2<k_1。由(a),(b)可知:j_1优于j_2优于j_3。 (2).k_2⩽k_0<k_1。由(a),(b)可知:j_1和j_3均优于j_2。 (3).k_2<k_1⩽k_0。由(a),(b)可知:j_3优于j_2优于j_1。
可以发现,对于这三种情况,j_2 始终不是最优解,于是我们可以将 j_2 从候选决策点中踢出去(删除),只留下 j_1 和 j_3,删后的情况如下图所示:
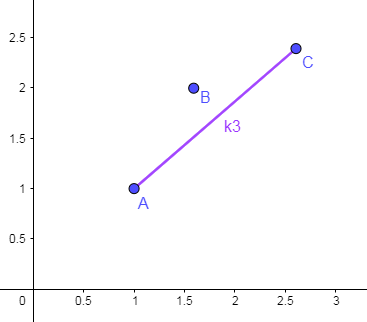
我们要对某一个问题的解决方案进行优化改进,无非就是关注两个要点:正确性 和 高效性 (很多时候 高效性 都体现为 单调性 )。
酱紫做的 正确性 是毋庸置疑的,因为在 j_1 和 j_3 其中必定有一个比 j_2 更优,所以删除 j_2 对答案没有任何影响。
那么高效性呢?自己在脑子里面 yy 一下,在一个坐标系的第一象限中(本题中 X(j) 和 Y(j)均大于等于 0,至于为什么这里要说等于,下面会提到),有若干个离散的点,任取三点,如果左边斜率大于右边斜率,则形成了上述情况,必定会 删点 ,因而消除这种情况。所以将最后留下来的点首位相连,其形成的各个线段 斜率 从左到右 必定是 单调递增 的(有可能非严格递增,这个问题之后再讨论)。
如果学习过计算几何相关知识,会意识到这个过程其实与求凸包算法是类似的。(顺手丢一个广告:【学习笔记】计算几何全家桶)
实际上在图中选取最靠左下面、下面、右下面的点首位相连,就是最后留下来的点了,它们形成了一个 下凸包,即 凸包(又名 凸壳)的下半部分(不严谨的讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的 凸多边形,它能包含点集中所有的点——摘自 百度百科)。
维护出的图形如下图所示:
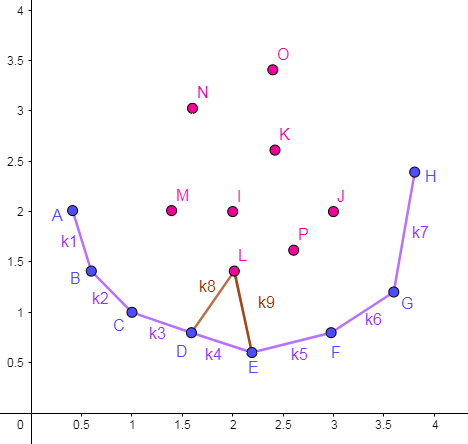
可以尝试在凸包围起来的区域内任意取一点,其必定能在包围圈上找到两个点使得该点可被删除。如上 L 点,它与 D,E 两点形成了一个 可删点图形 。
注意:图中
C,D,E故意画成了三点一线,而实际上点D是可以删去的,且严格凸包不允许存在这种情况。关于去重的细节问题后面会提到。
同理,如果把不等式 \large \frac{Y(j_2)−Y(j_1)}{X(j_2)−X(j_1)}⩽k_0[i] 改为 \large \frac{Y(j_2)−Y(j_1)}{X(j_2)−X(j_1)}⩾k_0[i] ,那么维护出来的就是一个 上凸包。
(2).【寻找最优决策点】
在一次决策点的寻找中,易知 下凸包 点集里总会存在一点,使得它与左邻点形成的斜率小于等于 k_0 ,与右邻点形成的斜率大于 k_0 。
例如上图中的 E 点,设 k_4⩽k_0<k_5 由于凸包上面的斜率呈 单增态,那么有:
\large k_1<k_2<k_3<k_4⩽k_0<k_5<k_6<k_7所以决策点 E 优于其他所有点,即 E 就是 dp[i] 的 最优决策点。
如果 暴力查找 的话,就是从第一个点开始向后扫描,找到 第一个斜率大于 k_0 的线段,其 左端点 即为 最优决策点。由于凸包上的 斜率依次递增,可以 二分 快速得到这个点。
2.【线性规划】
先回顾一下模板题的 dp 方程:
\large dp[i]=S[i]^2−2S[i]L+dp[j]+(S[j]+L)^2−2S[i] \times S[j]对其进行移项变化,变成形如 y=kx+b 的点斜式。
划重点:移项要遵循的原则是:把含有
function(i)∗function(j)的表达式看作斜率k_0乘以未知数x,含有dp[i]的项必须要在b的表达式中,含有function(j)的项必须在y的表达式中。如果未知数x的表达式单调递减,最好让等式两边同乘个−1,使其变为单增。
至于为什么说要让 x 的表达式单增,emm...其实是为了让一些较简单的问题模式化,不易出错,如果你非要单减,可以尝试倒序枚举,至于是否正确,具体实现需要注意的玄学问题等等,因为觉得太麻烦没有细想,我也不清楚会遇到什么问题。
例如此题,原 dp 方程可化为:
\large (2S[i])S[j]+(dp[i]−S[i]^2+2S[i]L)=(dp[j]+(S[j]+L)^2)其中 \large k_i=2S[i], x_i=S[j], b_i=dp[i]−S[i]^2+2S[i]L, y_i=dp[j]+(S[j]+L)^2
其实也可以化为:
\large (2S[i])(S[j]+L)+(dp[i]−S[i]^2)=(dp[j]+(S[j]+L)^2)其中 \large k_i=2S[i], x_i=S[j]+L, b_i=dp[i]−S[i]^2, y_i=dp[j]+(S[j]+L)^2
还可以化为 ... ...
只要满足上述移项原则,对答案是没有任何影响的。
这里以第一种形式为例,先画出草图:
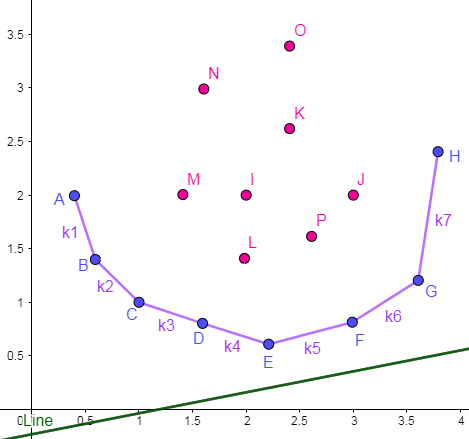
(1).【高中数学知识】
我们的目的是求出一个最优决策点 j 使得 dp[i] 最小,又因为 b[i]=dp[i]−S[i]^2+2S[i]L ,所以就是要找到某个点使这条直线经过它时算出来的 b 最小,即是高中数学课本上的线性规划问题。
(2).【寻找最优决策点】
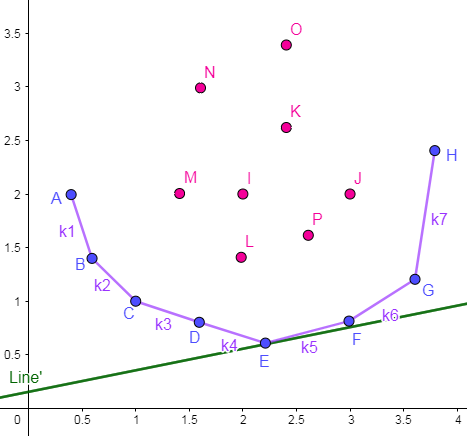
如图所示,点 E 即为 最优决策点。显然,这个使得 b 最小的最优决策点位于下凸包点集中,且与上述代数法求得的点一致。
3.【两种思考方式的结合】
强烈推荐用 线性规划 思想主导思考过程,因为图形的变幻较直观,更重要的是:在某某变量不满足单调性时,通过图形可以迅速做出判断并改变策略(在后面【关于单调性的研究】中会详细解释)。
而 代数法 通常在不便于识别方程特征时起一个转换思维方向的作用,因为有些题可能会直接出现 \frac{Y(j)−Y(j′)}{X(j)−X(j′)} 的形式,需要通过一系列代数推导后再绘草图模拟决策。
二.【维护凸包】
实际上只要让维护的凸包方向相同,两种思考方式的代码是一模一样的。
用单调队列维护凸包点集,操作分三步走:
- (1). 进行 择优筛选 时,在凸包上找到 最优决策点
j。 - (2). 用 最优决策点
j更新dp[i]。 - (3). 将
i作为一个决策点加入图形并更新凸包(如果点i也是dp[i]的决策点之一,则需要将(3)换到最前面)。
在本题中步骤 (3) 的具体操作为:判断当队尾的点与点 i 形成可删点图形时,出队直至无法再删点,然后将 i 加入队列。
在判断可删图形时有两种方法(以 下凸包 为例),一种是 slope(Q[t-1],Q[t])<=slope(Q[t],i),另一种是 slope(Q[t-1],Q[t])<=slope(Q[t-1],i),都表示出现了可以删去点 Q[t] 的情况(只要对边界、去重的处理足够严谨,两种写法是没有区别的)。其中 Q 是 维护凸包点集 的 队列。
该做法时间复杂度为 O(nlogn),瓶颈在于二分寻找最优决策点。
三.【再优化】
运用 决策单调性 进行优化。决策单调性 相关基础知识见 【学习笔记】动态规划—各种 DP 优化,这里只放一下定义:
设 j_0[i] 表示 dp[i] 转移的 最优决策点,那么决策单调性可描述为 ∀i⩽i′,j_0[i]⩽j_0[i′]。也就是说随着 i 的增大,所找到的 最优决策点是递增态(非严格递增)。
(1).【决策单调性证明】
还是以 玩具装箱 为例,来简单证一波 决策单调性,方法采用 四边形不等式。
四边形不等式 不知道是个啥,先去学习一下,然后继续。 2022.09.30
TODO