|
|
##[$POJ$ $3694$ $Network$](http://poj.org/problem?id=3694)
|
|
|
|
|
|
### 一、题目大意
|
|
|
|
|
|
$n$个点,$m$个边,连通图。
|
|
|
|
|
|
点与点之间通过边连接,如果切断某个边使得有点与其他点连接断开(连通分支增加),则称这种边为 **桥梁**(离散上叫 **割边**)。
|
|
|
接下来有$Q$个操作,每操作一次,也就是 **连接** 某条边后,**输出当前存在的桥梁数量**。
|
|
|
|
|
|
### 二、样例分析
|
|
|
|
|
|
我们看这个
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
4 4
|
|
|
1 2
|
|
|
2 1
|
|
|
2 3
|
|
|
1 4
|
|
|
2
|
|
|
1 2
|
|
|
3 4
|
|
|
0 0
|
|
|
```
|
|
|
|
|
|

|
|
|
|
|
|
一开始是图中蓝色部分,其中$1$和$4$之间的边,$2$和$3$之间的边称之为 **桥**,再加入$1\sim 2$边后(绿色),桥还是那俩没变,再加入$4\sim 3$边后,桥的数量为$0$(因为此时你去掉任何一个边,任意两个点都可连接)
|
|
|
|
|
|
|
|
|
### 二、解题思路
|
|
|
|
|
|
- ① 运行一次$Tarjan$,求出哪些边是割边。
|
|
|
- ② 两点连接起来,找这两个点的$LCA$,因为从点$u$到$LCA$再到点$v$再到点$u$,将形成环,里面的割边都会变成不是割边。
|
|
|
- ③ 计数的时候注意,随着新边的加入,有些树边已经被标记了,不再重复计数。
|
|
|
|
|
|
|
|
|
### $Code$
|
|
|
```cpp {.line-numbers}
|
|
|
#include <cstdio>
|
|
|
#include <iostream>
|
|
|
#include <algorithm>
|
|
|
#include <cstring>
|
|
|
|
|
|
using namespace std;
|
|
|
const int M = 400010;
|
|
|
const int N = 100010;
|
|
|
|
|
|
int bridge[N]; // 某个节点的入边是不是桥,比如 u->v是桥,则记录bridge[v]=1
|
|
|
int p[N]; // 并查集
|
|
|
int bcnt; // 桥的数量
|
|
|
|
|
|
int n, m;
|
|
|
// 链式前向星
|
|
|
int e[M], h[N], idx, w[M], ne[M];
|
|
|
void add(int a, int b, int c = 0) {
|
|
|
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
|
|
|
}
|
|
|
|
|
|
// Tarjan算法求割边模板
|
|
|
int dfn[N], low[N], ts;
|
|
|
void tarjan(int u, int fa) {
|
|
|
dfn[u] = low[u] = ++ts;
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int v = e[i];
|
|
|
if (v == fa) continue;
|
|
|
|
|
|
if (!dfn[v]) {
|
|
|
p[v] = u; // 记录v的父节点是u
|
|
|
tarjan(v, u); // 先搜索子树v
|
|
|
low[u] = min(low[u], low[v]);
|
|
|
if (low[v] > dfn[u]) { // 发现割边
|
|
|
bcnt++; // 割边数量 +1
|
|
|
bridge[v] = 1; // 因为经Tarjan算法缩点后,是一棵树,所以,bridge[v]代表的就是父节点向v的边,也就是u->v的边是割边
|
|
|
}
|
|
|
} else
|
|
|
low[u] = min(low[u], dfn[v]);
|
|
|
}
|
|
|
}
|
|
|
|
|
|
// 暴力方法找到lca(a,b)
|
|
|
int lca(int a, int b) {
|
|
|
if (dfn[a] > dfn[b]) swap(a, b); // 利有dfn的物理含义,可以知道a和b的最终生成树中的深度关系
|
|
|
|
|
|
// 本题与什么缩点没有一毛钱关系,只是在讨论割边。
|
|
|
// 整体思路就是用Tarjan算法求出割边,然后尝试连接(a,b),如样例的图所示
|
|
|
// b节点,满足b在a下面就一直向上,直到不能再上,再上就跑到a上面去了为止
|
|
|
// 对于两个深度的节点a,b,先将a,b对齐到同一高度
|
|
|
while (dfn[a] < dfn[b]) {
|
|
|
if (bridge[b]) bcnt--;
|
|
|
bridge[b] = 0;
|
|
|
b = p[b];
|
|
|
}
|
|
|
// 然后再两个节点一起向上跳,这是为了照顾效率吗?
|
|
|
while (a != b) {
|
|
|
if (bridge[a]) bridge[a] = 0, bcnt--; // 如果p[a]->a是割边的话,那么现在因为有了环,将不再是割边
|
|
|
if (bridge[b]) bridge[b] = 0, bcnt--; // 如果p[b]->b是割边的话,那么现在因为有了环,将不再是割边
|
|
|
a = p[a], b = p[b]; // 一路向上
|
|
|
}
|
|
|
|
|
|
return a;
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
#ifndef ONLINE_JUDGE
|
|
|
freopen("POJ3694.in", "r", stdin);
|
|
|
#endif
|
|
|
int cas = 0;
|
|
|
while (~scanf("%d%d", &n, &m)) {
|
|
|
if (n == m && n == 0) break;
|
|
|
|
|
|
ts = bcnt = 0;
|
|
|
memset(h, -1, sizeof h); // 初始化链式前向星
|
|
|
memset(low, 0, sizeof low); // 初始化Tarjan算法需要的数组
|
|
|
memset(dfn, 0, sizeof dfn); // 初始化Tarjan算法需要的数组
|
|
|
memset(bridge, 0, sizeof bridge); // 记录某条边是不是桥
|
|
|
for (int i = 1; i <= n; i++) p[i] = i; // 初始化并查集
|
|
|
|
|
|
printf("Case %d:\n", ++cas);
|
|
|
while (m--) {
|
|
|
int a, b;
|
|
|
scanf("%d%d", &a, &b);
|
|
|
add(a, b), add(b, a);
|
|
|
}
|
|
|
|
|
|
// 因为是无向则连通的图,所以所有点必然都连通,也就是从1号点可以到达任意点,
|
|
|
// 不需要枚举每个点,并且判断dfn[i]==0进行判断
|
|
|
tarjan(1, 0);
|
|
|
|
|
|
// q次询问
|
|
|
int q;
|
|
|
scanf("%d", &q);
|
|
|
while (q--) {
|
|
|
// 添加边,如果边的两端处在不同的点上,求他们的LCA,并且减少桥的数量
|
|
|
int a, b;
|
|
|
scanf("%d%d", &a, &b);
|
|
|
lca(a, b);
|
|
|
printf("%d\n", bcnt); // 割边数量
|
|
|
}
|
|
|
puts("");
|
|
|
}
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
### 三、总结
|
|
|
- ① $Tarjan$ 计算割边,可以用`set<int,int> _set` 记录$u->v$是割边;同时,由于$Tarjan$执行边双缩点后,最终是一棵树,所以,也可以用$bridge[v]$来描述$fa[v]->v$这条边是割边,因为树的父节点向子节点只有一条边,记录到$v$身上就可以配合树的遍历找到这条割边。
|
|
|
|
|
|
- ② $Tarjan$ 算法在本质上是一个$dfs$的过程,产生的$dfs$序$dfn[i]$可以理解为$LCA$中的深度概念,配合暴力的$lca$求解办法,不断向上,直到找出$lca(u,v)$
|
|
|
|
|
|
- ③ 为什么本题不将图用$bfs$预处理,然后通过倍增$lca$来求解$lca$呢?
|
|
|
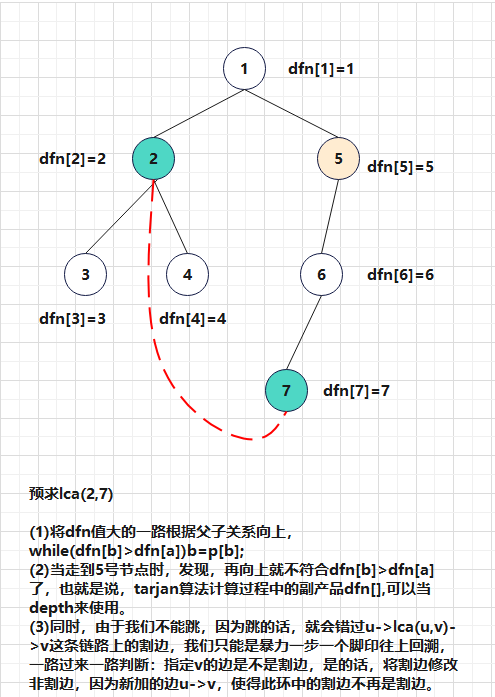
答:因为倍增讲究一个跳字,能多跳不少跳。而本题,割边可能存在于$u \Rightarrow
|
|
|
lca(u,v) \Rightarrow v$这条链路上的每一个位置,如果跳过,就无法将每次添加边后环中遇到的割边修改为非割边。只能是一步一步向上,不能跳着走。
|
|
|
|
|
|
|
|
|
 |