You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
2.1 KiB
2.1 KiB
HDU~3394 Railway
题目大意
N个点,M条即将要修建的铁路。现在问,为了环形游览N个点。问我们有多少条路径是冲突的。定义冲突路径为:它不仅仅包含于一个环里面。如果一条路径不属于任何一个环,那么没有必要修建它。询问我们不必要修建的铁路数和冲突的铁路数。
题目思路
显然不必要修建的铁路数就是该无向图中桥的数目。为什么?
割边 不在任意一个简单环上,所以求割边即可。
对于一个环中的边,我们移除任意一条边,仍然可以实现环中节点可达性。如果一个图移除掉了桥,其连通分量会增加。即桥不包含于任何一个环,因此没必要修建为桥(割边)的铁路。
而对于冲突边,其必然在点双连通分量中出现,如果一个块的点数等于边数,说明其是一个环,没有冲突边,但如果边数大于点数,说明这个块里至少有两个环,简单分析知此时块内所有边均为冲突边,所以问题转变为求桥的数量以及每个块的点数和边数,用Tarjan求点双连通分量,顺便就可以求出桥数,每找到一个块,就统计块内点的数量以及这些点之间连的边数,判断边数是否大于点数,如果大于则将边数累加到答案中
结论 一个点双连通分量中,若边的个数 > 点的个数 , 则边双中每个点都至少处于两个简单环上.
- 点
=边+ 1 \Rightarrow两点一线 - 点
=边\Rightarrow简单环 - 点
<边\Rightarrow环套环 (大环套小环)
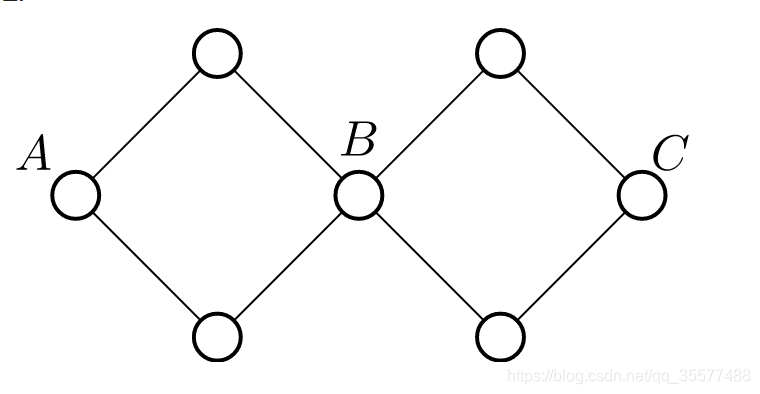
Q:那为什么不能是边双呢? 如下图所示:
这个边双的点的个数 < 边的个数。但他们并不是任意一条边都在至少两个简单环以上.