5.2 KiB
https://blog.csdn.net/weixin_43848437/article/details/105133155
DFS 树
介绍
这是一篇对可以用图的 DFS 树来解题的教程/扩展。
在很长一段时间,我并没有真正理解传统算法是如何找到 桥 的。很多题解看起来没有真正解释它是如何工作的,很多只是顺带提到它但后迅速地进入实现部分。某一天有人解释了 DFS 树是什么, 我才终于正确地理解了它。在此之前,我花了很长时间去理解寻找桥的算法,而且我经常要注意一些细节。现在我已经可以用打字的速度去实现它了。
但是更重要的是,我开始明白同样的算法该如何用在与桥或多或少无关的题目上。这件事,就像当你有一个黑盒时,你只可以把它当作一个黑盒去使用。但如果你有一个你十分了解的盒子,你可以把它分解,略加改动并把它用在完全不同的事情上,并且毫无疏漏。
就我而言,DFS 树是我所知的解决图的结构问题最好的算法之一。此外,有时在你使用 DFS 树后,一些可疑的贪心算法的正确性也会变得显而易见。
DFS 树
考虑一个无向连通图 G,对它进行深度优先遍历。它可以用一个递归函数来实现,就像这样:
function visit(u):
mark u as visited
for each vertex v among the neighbours of u:
if v is not visited:
mark the edge uv
call visit(v)
以下是实现过程的动画:
我们看一下在第 5 行被标记的边。他们构成 G 的以 1 为根的生成树。我们称这些边为 树边, 其他的所有边为 回边。
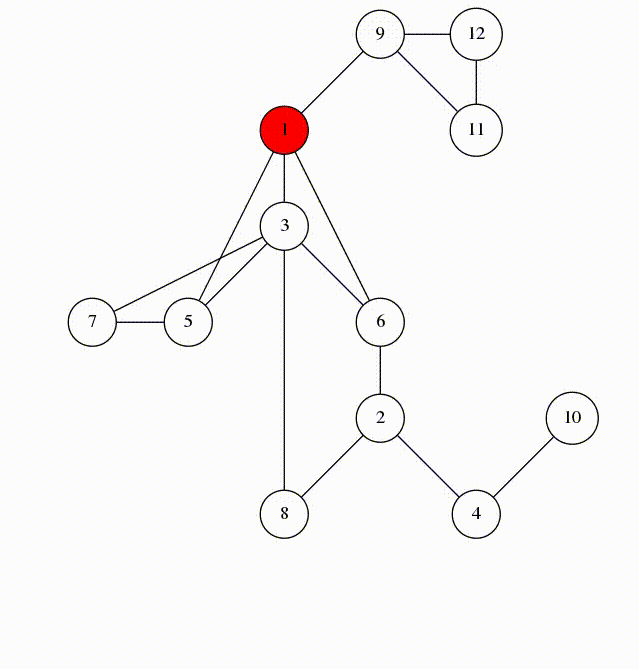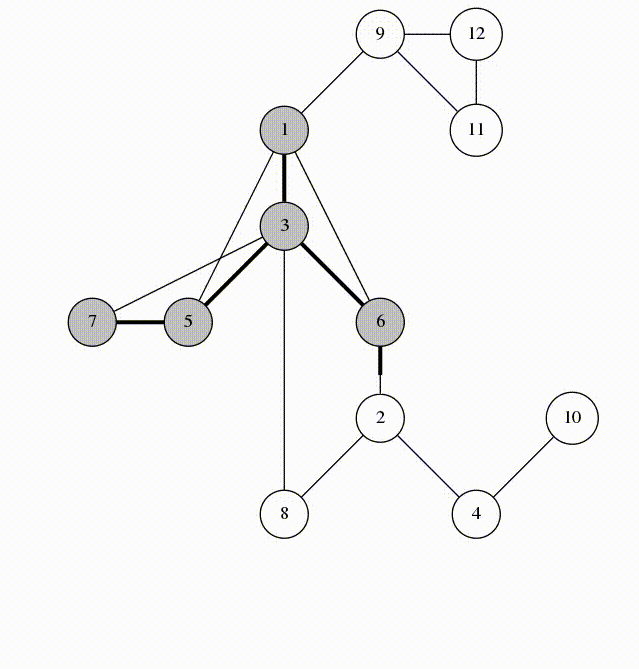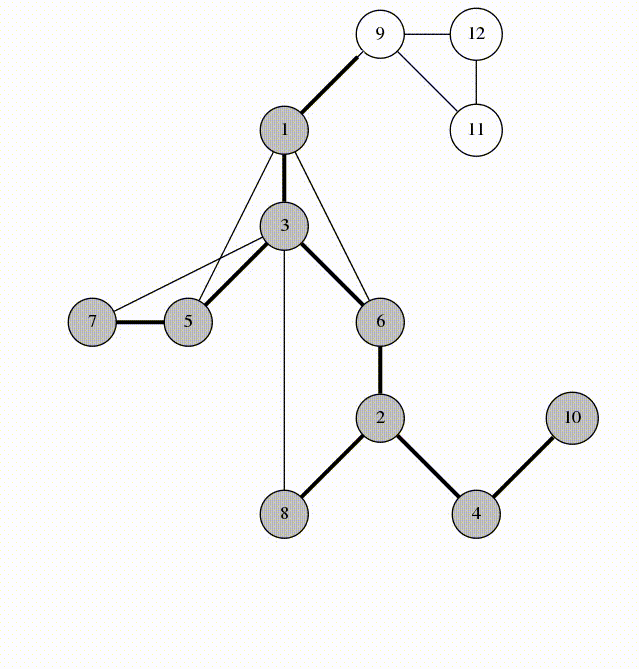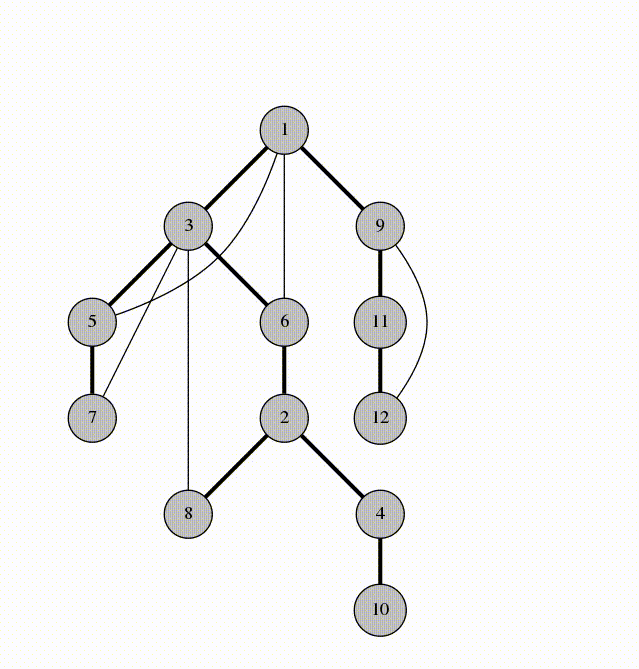
这就是我们图的 DFS 树:
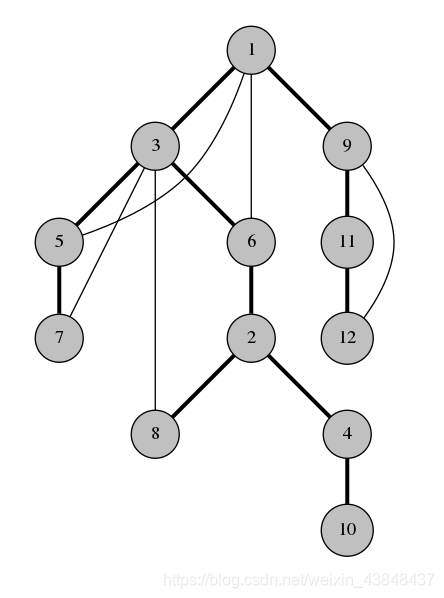
结论 1:在生成树中,图的回边连接的都是一个顶点和它的子孙节点。这就是 DFS 树好用的原因。
证明:假设有一条边 uv,深度优先遍历已经访问了 u 但还没访问到 v。然后:
- 如果深度优先遍历沿着
uv边由u走向v,那么uv是一条树边 - 如果深度优先遍历没有沿着
uv从u访问v,然而此时遍历到第四步发现v已经被访问过了。说明v是在遍历u的一个邻居节点时对它进行了访问,这意味着v是u在DFS树中的一个子孙节点。
例如在上面的图中,节点 4 和节点 8不可能由一条回边相连因为它们各自都不是另一个的祖先节点,如果由一条边连接 4 和 8,遍历会从 4 走向 8 而不是返回 2。
这是 DFS 树最显而易见的结论。DFS 树如此有用是因为它简化了图的结构。与其去考虑图中所有种类的边,我们此时只需要考虑一棵树和一些额外的祖先-子孙连边。这样的结构十分适于思考和尝试算法。
找桥(或割点)
DFS 树和结论 1 是 Tarjan 找桥算法 的核心。传统的找桥教程只顺带提到了 DFS 树并从定义奇怪的 dfn[u] 数组和 low[u] 数组开始。把这些全部忘掉。这些是实现的细节,在我看来,它们甚至不是实现找桥算法最直观的方法。在找桥算法中,dfn[u] 只是一个用来确认某一顶点是否是 DFS 树中另一顶点的祖先的令人迷惑的方法。同时,也很难清楚地解释 low[u] 代表着什么。
以下就是在一个无向连通图中找桥的方法。考虑图 G 的 DFS 数。
结论 2:当且仅当树边 uv 不存在连接其祖先和子孙节点的回边时,它是桥。也就是说,树边 uv 是桥当且仅当此时没有回边跨越它。
证明:移出边 uv 将生成树分成了两个互补连接的部分:uv 的子树和剩余的生成树。如果两部分间有回边相连,那么图依旧连通,否则 uv 就是个桥。回边连接这两部分的唯一情况就是它连接了 uv 的祖先和子孙
例如,在上图的 DFS 树中,连接 6 和 2 的不是桥, 因为即使我们移除了它,连接 3 和 8 的回边依旧使图连通。看另一个例子,连接 2 和 4 的边是桥,因为并没有跨越它的回边来使图在移除 2-4 边后继续连通。
结论 3:回边一定不是桥。
这引出了经典的找桥算法。考虑一个图 G:
1.建立这张图的 DFS 树。
2.对每一条树边 uv,寻找是否有一条回边跨越uv,如果没有,它就是桥。
因为 DFS 树的简单结构,第二步十分容易实现。例如,你可以用传统的 low[u] 方法;或者,可以用 前缀和 来记录,这就是我推崇的。
我们用dp[x]表示: 多少条回边穿过x - fa[x]。
自下往上转移dp。
\large dp[x]=dp[y_i] + (x-> 其祖先节点 的回边的个数) - ( x的后代节点连接x的回边个数 )最后只要dp[x]等于0,那么x与其父亲节点连接的边,一定是桥边。