python

7.0 KiB

Raw Permalink Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

`AcWing` `300`. 任务安排`1`

一、题目描述

有 N 个任务排成一个序列 在一台机器上 等待执行，它们的顺序不得改变。

机器会把这 N 个任务分成若干批，每一批包含连续的若干个任务。

从时刻 0 开始，任务被分批加工，执行第 i 个任务所需的时间是 T_i。

另外，在每批任务开始前，机器需要 S 的启动时间，故执行一批任务所需的时间是启动时间 S 加上每个任务所需时间之和。

一个任务执行后，将在机器中稍作等待，直至该批任务全部执行完毕。

也就是说，同一批任务将在同一时刻完成。

每个任务的费用是 它的完成时刻乘以一个费用系数 C_i。

请为机器规划一个分组方案，使得总费用最小。

输入格式 第一行包含整数 N。

第二行包含整数 S。

接下来 N 行每行有一对整数，分别为 T_i 和 C_i，表示第 i 个任务单独完成所需的时间 T_i 及其费用系数 C_i。

输出格式 输出一个整数，表示最小总费用。

数据范围 1≤N≤5000,0≤S≤50,1≤T_i,C_i≤100

输入样例：

输出样例：

###　二、理解用例

假如这样分组：

最佳答案是153，我们现在算出来是163，很显然这不是最优的办法。

最优的解是这样的：

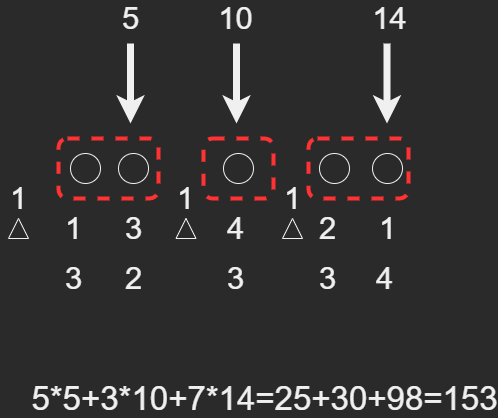
二、暴力枚举`MLE`

空间复杂度O(n^2)、时间复杂度O(n^3)

状态表示：

集合:f[i][j]表示前i个任务分成j组的集合
属性:最小费用

状态计算：

\large f[i][j]=min(f[k][j−1]+(j×s+\sum_{a=1}^{i}t[i])×(\sum_{a=k+1}^ic[i])),k \in [j-1,i)

最后一个不同点：最后一组，枚举最后一组的起点：可以分为前k个机器分为j−1组，k+1 \sim i个机器是第j组

\displaystyle \sum_{a=1}^i t[i]和\displaystyle \sum_{a=k+1}^{i}c[i]可以用前缀和优化

暴力代码

#include <bits/stdc++.h>

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 5010;
int t[N], c[N];
int f[N][N];
int n, s;
/**
 5
1
1 3
3 2
4 3
2 3
1 4

 答案：153

 二维数组：
 5000*5000=25000000

 25000000 * 4byte=100000000 byte = 100000 kb =  100 mb >题目要求的64mb ，所以不出意外：
 MLE了！还没有来的及TLE，先MLE了！看来需要一个一维的状态表示方法！
 */
int main() {
    // 任务个数与启动时间
    cin >> n >> s;

    for (int i = 1; i <= n; i++) {
        cin >> t[i] >> c[i];
        t[i] += t[i - 1]; // t数组自带前缀和
        c[i] += c[i - 1]; // c数组自带前缀和
    }

    /* 1、为什么这样初始化？
      答：看状态转移方程
      f[i][j] = min(f[i][j], f[k][j - 1] + (j * s + t[i]) * (c[i] - c[k]));
      f[i][j]：前i个任务，在j个阶段的场景下，最小的代价值是多少。

      这个k好说，有上面的循环限制了它的范围。
      这个j-1就要小心了，不能小于零吧~，而且，如果等于0是啥意思，也要从现实意义出发进行初始化设置
      j-1=0,也就是说在第0个阶段，第0个阶段就是还没有开始,管你前多少个任务，代价值都应该是0
     */
    memset(f, 0x3f, sizeof f);
    memset(f[0], 0, sizeof f[0]);

    // 2、开始填表
    for (int i = 1; i <= n; i++)                                                      // i个任务
        for (int j = 1; j <= i; j++)                                                  // j个阶段，注意j的上界，一个阶段1个任务是极限，此时i=j
            for (int k = j - 1; k < i; k++)                                           // 最后一个阶段的起点k
                f[i][j] = min(f[i][j], f[k][j - 1] + (s * j + t[i]) * (c[i] - c[k])); // 前缀和 \sum_{a=k+1}^{i}c[a]

    /*
     3、收集答案
     f[n]表示在n个任务,那么划分的分组数量可能是多少呢？是1，2，3，...n,其中1表示全部划归一组,n表示一个任务一组，共n组
    */
    int res = INF;
    for (int i = 1; i <= n; i++) res = min(res, f[n][i]);
    cout << res << endl;
    return 0;
}

四、优化：费用提前计算

为什么要写暴力?

所有题目拿下来都可以先向暴力的方向去想，然后再进行优化

进一步思考

我们为什么要枚举每一组？是为了得到启动机器的次数进而算费用我们可以发现，只要我们分一组，后面还未分组的机器一定会增加相应的费用，高兴的是我们现在就可以算出来增加的费用是多少，所以我们只需要提前把这个多出来的费用加上就行了

状态表示：

集合:f[i]表示前i个任务处理完的所有方案的集合

不关心划分成多少个组

属性:最小费用

考虑最后一个不同点

假设当前正在思考f[i],它前面的最后一个任务终点j在哪里,很明显，j \in [0,i),i在最后一组中。

当在j+1处创建一个新的分组时，那么后续的所有任务，都将增加S的时间，总共的增加时长=(c[n]-c[j])\times s

状态转移方程：

\large f[i]=min(f[j]+(c[i]−c[j])×t[i]+(c[n]−c[j])×s), j \in [0,i)

同上c[i]和t[i]是前缀和。

四、`AC`代码

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 5010;
int n;   // n个任务
LL s;    // 等待时间
LL c[N]; // 每个任务都有一个花费，   用c[i]来表示,更新概念为前缀和
LL t[N]; // 每个任务都有一个执行时间,用t[i]来表示,更新概念为前缀和
LL f[N]; // 前i个任务，不管划分多少个阶段，最小代价是多少

int main() {
    cin >> n >> s;
    for (int i = 1; i <= n; i++) {
        cin >> t[i] >> c[i];
        t[i] += t[i - 1];
        c[i] += c[i - 1];
    }

    // 初始化
    memset(f, 0x3f, sizeof f);
    f[0] = 0;

    for (int i = 1; i <= n; i++)    // 从小到大枚举每个任务
        for (int j = 0; j < i; j++) // j:前一个批次的最后一个位置
            f[i] = min(f[i], f[j] + t[i] * (c[i] - c[j]) + s * (c[n] - c[j]));
    // 输出
    cout << f[n] << endl;
    return 0;
}

7.0 KiB Raw Permalink Blame History Unescape Escape

AcWing 300. 任务安排1