python/TangDou/AcWing/BinarySearch/AGC006D.md

##AGC006D Median Pyramid Hard

一、题目描述

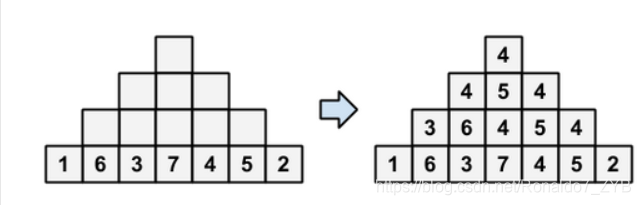
二、题目解析

这道例题看到时毫无头绪，因为课程是二分，所以往二分的方向想，猜到是 二分枚举最上面的那个数是多少，但依然不会做。

事实上，因为我们求得是 中位数，所以每个数对我们来说 只有与枚举的数的大小关系 需要我们考虑，我们可以使大于等于这个数的数为1，小于的为0。

如此将其转化成一个01串，接下来我们讨论这个01串。

接下来我们可以小小的推一下, 事实上，当有两个都为0的数或者都为1的数，就可以一直往上走:

假设有这样一个 0 1 数列

    0  1  1  0  1

然后推，会变成这样

	1 
     1  1  1  
  0  1  1  0  1

我们可以发现如果有多个1或0连在一起，那么他们就无法被分开，他会一直往上走。

似乎我们只要找到相邻一样的就可以了。

还是给一张 Atcoder 题解的例图:

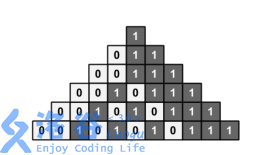
我们只需要找到离中间最近的一组相邻一样的两个数，就可以得到最上面是什么数,也就是说，最后那组先走到顶那组就赢了，那就要看那组离中心更近。

那会不会存在两个不同阵营的组距离一样远呢，你会发现这是不可能的。

因为，如果距离相等，那么中间一定是奇数个位置，我们用1和0,交替隔开两组，那么最后一个位置肯定会和左边或者右边一样，又形成一个组，所这两个组要么都是1，要么都是0。

最后还有一种特殊情况。就是没有任何两个相邻的:

我们只需要特判一下就行了。

三、实现代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 200100;
int a[N], n;

/*
二分塔顶的值，把大于等于这个值的变为1，小于变为0
可以发现如果有多个1或0连在一起，那么他们就无法被分开，他会一直往上走
也就是说，最后那组先走到顶那组就赢了，那就要看哪组离中心更近

那会不会存在两个不同阵营的组距离一样远能，你会发现这是不可能的:
因为，如果距离相等，那么中间一定是奇数位置，我们用1和0,交替隔开两组，那么最后一个位置肯定会和左边或者右边一样，又形成一个组，所这两个组要么都是1，要么都是0
*/
bool check(int x) {
    //从中间向两边开始查找连续的0或1
    for (int i = 0; i <= n - 1; i++) {
        //左侧存在连续0,或者，右侧存在连续0,那么最终结果肯定为0，这与我们事先约定的塔顶元素是x,大于等于x 的都是1，出现矛盾，说明我们给的x不对，数字1太少了，x给大了，需要减小x
        if ((a[n - i] < x && a[n - i - 1] < x) || (a[n + i] < x && a[n + i + 1] < x)) return false;
        //左侧存在连续1，或者，右侧存在连续1，那么最终结果肯定为1，符合我们事先的约定,数字1数量够用，可以再把x调大一点
        if ((a[n - i] >= x && a[n - i - 1] >= x) || (a[n + i] >= x && a[n + i + 1] >= x)) return true;
    }

    //如果一路检查都没有找到连续的0和1 ，说明是特例情况:
    // 0101 0 1010
    // 1010 1 0101
    // 这样的东东,最左(右)下角的值>=塔顶值
    return a[1] >= x;
}

int main() {
    //加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    cin >> n;
    for (int i = 1; i <= 2 * n - 1; i++) cin >> a[i]; //全排列

    int l = 1, r = 2 * n - 1;
    while (l <= r) {
        int mid = (l + r) >> 1;
        if (check(mid))
            l = mid + 1;
        else
            r = mid - 1;
    }

    printf("%d\n", l - 1);
    return 0;
}