4.2 KiB
一、题目描述
给定一个浮点数 n,求它的三次方根。
输入格式
共一行,包含一个浮点数 n。
输出格式 共一行,包含一个浮点数,表示问题的解。
注意,结果保留 6 位小数。
数据范围
−10000≤n≤10000
输入样例:
1000.00
输出样例:
10.000000
二、理解与感悟
浮点数二分还是很简单的,最开始使劲设置最大和最小,精度一般设为1e-8,然后根据条件写check(),发现符合就向左或向右逼近,直到结果的差,精度在可以接受的范围内,完事。
三、C++代码
#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-8;
int main() {
double x;
cin >> x;
cin >> x;
double l = -10000, r = 10000;
while (r - l > eps) {
double mid = (l + r) / 2; // 注意:浮点数这里不能用右移1位!!
if (mid * mid * mid > x)
r = mid; // mid>x后面没有"="
else
l = mid;
}
printf("%.6lf\n", l);
return 0;
}
四、牛顿迭代法
概述
牛顿迭代法 是非常高效的求解方程的根的方法。其求解原理可以参考各文献。大体的思路如下:
通过不断地做切线来逼近真实的根,直到误差小于精度。
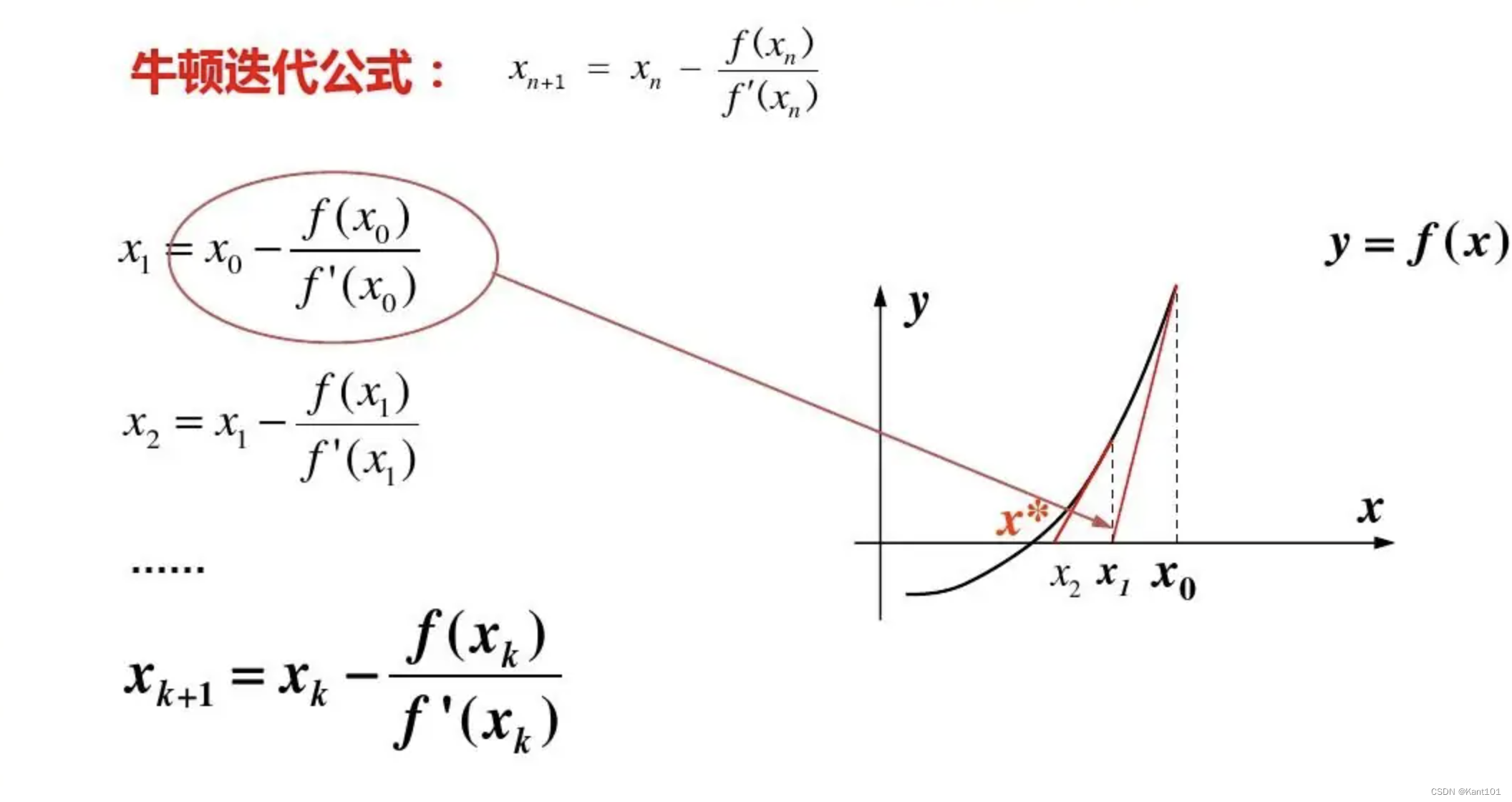
可得迭代公式:
\large x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}通过这种不断地做切线的方法,直到 ∣x_n − x_∗∣ < 给定的精度,在误差范围内可以认为 x_n 就是方程的根了。
牛顿法求平法根
假设我们要求解n的平方根,那么我们可以构建函数f(x)=x^2-n。那么方程 x^2-n=0 的理论根为 x=\sqrt{n} ,即求解这个方程得到的根就是求的n的平方根。
例如求5的平方根,那么可以构建函数 f(x)=x^2-5,方程 x^2-5=0 的理论根即为 \sqrt{5} ,在误差范围内,用牛顿法求解出方程 x^2-5=0 的根即可认为是5的平方根。
迭代公式
构建函数
f(x)=x^2-n
那么有:
f'(x)=2x
根据牛顿法的迭代公式有:
\large x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}=x_n-\frac{x_n^2-n}{2x_n}=\frac{x_n+n/x_n}{2}
牛顿法求多次方根
跟求平方根同理,只是构建的函数不同,例如求解m次方根,那么就需要构建函数
f(x)=x^m −n
那么就有:
f'(x)=m∗x^{m−1}
根据牛顿法的迭代公式有:
\huge x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}= x_n-\frac{x_n^m-n}{m*x_n^{m-1}}
例如求解n的3次方根,那么就有:
\huge x_{n+1}=x_n − \frac{x_n^3-n}{3*x_n^2}=\frac{2x_n^3+n}{3*x_n^2}
例如求解n的4次方根,那么就有:
\huge x_{n+1}=x_n − \frac{x_n^4-n}{4*x_n^3}=\frac{3x_n^4+n}{4*x_n^3}
...
以此类推
实现代码
#include <bits/stdc++.h>
using namespace std;
/*
浮点数不能太大,10000>=a>=-10000
*/
double sqrt(int n) {
double x = n;
for (int i = 1; i <= 100; i++) x = (x * x + n) / (2 * x);
return x;
}
double sqrt3(int n) {
double x = n;
for (int i = 1; i <= 100; i++) x = (2 * x * x * x + n) / (3 * x * x);
return x;
}
double sqrt4(int n) {
double x = n;
for (int i = 1; i <= 100; i++) x = (3 * x * x * x * x + n) / (4 * x * x * x);
return x;
}
double sqrt5(int n) {
double x = n;
for (int i = 1; i <= 100; i++) x = (4 * x * x * x * x * x + n) / (5 * x * x * x * x);
return x;
}
int main() {
// 求n的平方根和立方根
double n;
cin >> n;
// 平方根
printf("%.6lf\n", sqrt(n));
// 立方根
printf("%.6lf\n", sqrt3(n));
// 4次方根
printf("%.6lf\n", sqrt4(n));
// 5次方根
printf("%.6lf\n", sqrt5(n));
return 0;
}