python/TangDou/AcWing/BeiBao/487.md

##AcWing 487. 金明的预算方案

一、题目描述

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。

更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过N元钱就行”。

今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

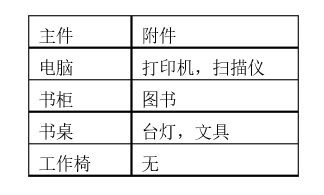
如果要买归类为附件的物品，必须先买该附件所属的主件。

每个主件可以有0个、1个或2个附件。

附件不再有从属于自己的附件。

金明想买的东西很多，肯定会超过妈妈限定的N元。

于是，他把每件物品规定了一个重要度，分为5等：用整数1\sim 5表示，第5等最重要。

他还从因特网上查到了每件物品的价格（都是10元的整数倍）。

他希望在不超过N元（可以等于N元）的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第j件物品的价格为v[j]，重要度为w[j]，共选中了k件物品，编号依次为j_1，j_2，…，j_k，则所求的总和为：

v[j_1]∗w[j_1]+v[j_2]∗w[j_2]+…+v[j_k]∗w[j_k]

（其中*为乘号）

请你帮助金明设计一个满足要求的购物单。

输入格式 输入文件的第1行，为两个正整数，用一个空格隔开：N m，其中N表示总钱数，m为希望购买物品的个数。

从第2行到第m+1行，第j行给出了编号为j-1的物品的基本数据，每行有3个非负整数v p q，其中v表示该物品的价格，p表示该物品的重要度（1~5），q表示该物品是主件还是附件。

如果q=0，表示该物品为主件，如果q>0，表示该物品为附件，q是所属主件的编号。

输出格式 输出文件只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值（<200000）。

数据范围 N<32000,m<60,v<10000

输入样例：

1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0

输出样例：

2200

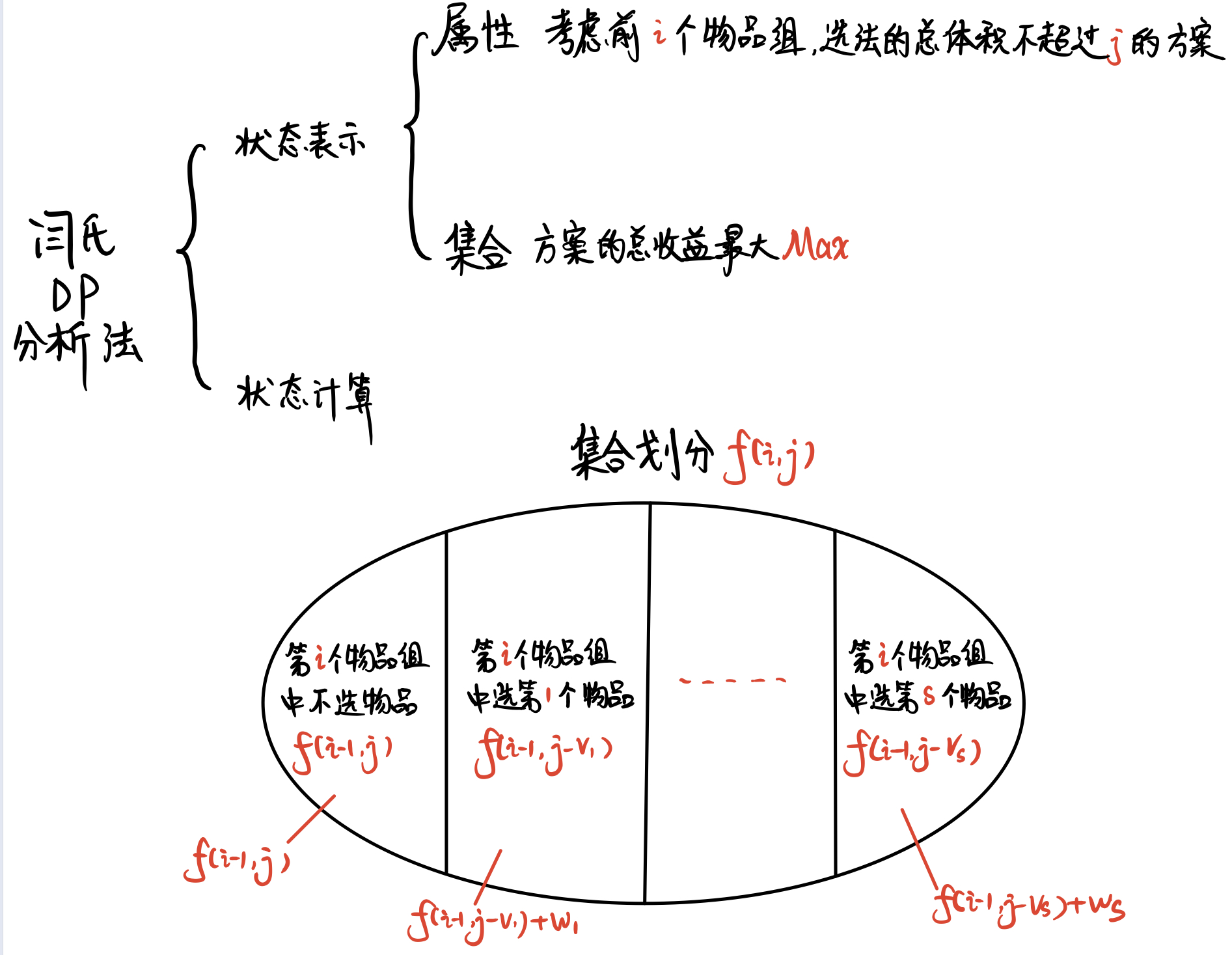
二、分组背包解法

直接上 分组背包 的 闫氏DP 分析法

初始状态 ：f[0][0]

目标状态 ：f[N][M]

状态表示

f[i][j] 从前 i 组物品中选择且总体积不大于 j 的最大价值

状态计算

针对第 i 组物品，将整个状态划分成 s[i]+1 类：

• 第i组物品一个都不要：f[i][j] = f[i-1][j]
• 选第 i 组物品的第一个物品：f[i][j] = f[i-1][j-v[1]]+w[1]
• 选第 i 组物品的第二个物品：f[i][j] = f[i-1][j-v[2]]+w[2]
• 选第 i 组物品的第 k 个物品：f[i][j] = f[i-1][j-v[k]]+w[k]

状态转移

$$\large f[i][j]=max(f[i][j], f[i-1][j-v[k]]+w[k])), k=0, 1, 2,...,s[

状态初始化

f[0][0\sim m] = 0 表示在选择 0 件物品时对于任何体积来讲，其最大价值均为 0

####前导知识 AcWing 9. 分组背包问题

(1) 打包的三种方法

#include <bits/stdc++.h>

using namespace std;

vector<string> a = {"1"};
vector<string> b = {"2", "3", "4"};

void dfs(int u, string s) {
    if (u == 3) {
        cout << s << " ";
        return;
    }
    dfs(u + 1, s);
    dfs(u + 1, s + "," + b[u]);
}

// 生成分组信息
int main() {
    // ①二进制枚举法【正规方法】

    // 因为手动录入了第一个元素，所以这里枚举避开了全不选的0
    int sz = b.size();
    for (int i = 1; i < 1 << sz; i++) { // 1~2^3.模拟每个数
        string t = a[0];
        for (int j = 0; j < sz; j++) // 每个数位
            if (i >> j & 1)          // 如果此位置为1,表示当前数字出现在组合中
                t = t + "," + b[j];
        a.push_back(t);
    }
    for (auto c : a) cout << c << " ";
    puts("");

    // ② dfs【一般推荐】
    dfs(0, a[0]);
    puts("");

    // ③ 多次循环法【不推荐】
    a = {"1"};
    b = {"2", "3", "4"};
    for (int i = 0; i < b.size(); i++) {
        sz = a.size();
        for (int j = 0; j < sz; j++)
            a.push_back(a[j] + "," + b[i]);
    }
    for (auto c : a) cout << c << " ";

    // 清空再来
    puts("");
    return 0;
}

(2) 二进制枚举法+分组背包模板

#include <bits/stdc++.h>

using namespace std;

// 利用二进制枚举进行分组
const int N = 60, M = 32010;

struct Node {
    int w, v;
};

int n, m;
vector<Node> a[N]; // 主件
vector<Node> b[N]; // 附件
int f[M];

int main() {
    cin >> m >> n;

    for (int i = 1; i <= n; i++) {
        int w, p, q;
        cin >> w >> p >> q;

        if (!q)
            a[i].push_back({w, p * w});
        else
            b[q].push_back({w, p * w});
    }

    // 利用二进制枚举，生成分组的所有组合情况
    for (int i = 1; i <= n; i++) {
        if (!a[i].size()) continue;                  // 只讨论主件，由主件进行构建
        for (int j = 0; j < 1 << b[i].size(); j++) { // 每一组子件的组合情况
            int v = a[i][0].v, w = a[i][0].w;
            for (int k = 0; k < b[i].size(); k++)
                if (j >> k & 1) v += b[i][k].v, w += b[i][k].w;
            // 组内选一个
            a[i].push_back({w, v});
        }
    }

    // 分组背包模板
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= 0; j--)
            for (int k = 0; k < a[i].size(); k++) // 注意：这里k是从0开始，因为vector的特点决定
                if (j >= a[i][k].w)
                    f[j] = max(f[j], f[j - a[i][k].w] + a[i][k].v);

    // 输出
    printf("%d\n", f[m]);
    return 0;
}

(3)分组背包模板

以主件为组数来分,一组内有以下选法； 选主件，选主件+附件1，选主件+附件2，主件+附件1+附件2； 那么我们将这四种方案分别打包，再跑分组背包的模板即可；

#include <bits/stdc++.h>
using namespace std;

// 利用循环法进行分组
const int N = 60, M = 32010;

struct Node {
    int w, v;
};

int n, m;
vector<Node> a[N]; // 主件
vector<Node> b[N]; // 附件
int f[M];

int main() {
    cin >> m >> n; // 容量上限，物品个数

    for (int i = 1; i <= n; i++) {
        int w, p, q;
        cin >> w >> p >> q;             // 体积,重要度，依赖哪个物品
        if (!q)                         // 如果是主件
            a[i].push_back({w, w * p}); // 记录主件i的列表中，有了only主件i这个东西
        else
            b[q].push_back({w, w * p}); // 记录主件q的列表中，有了一个附件
    }

    /*
    比如物品A是1个主件，2个附件，应该最后有4种组合： 主件；主件+附件1；主件+附件2; 主件+附件1+附件2;
    处理办法:
    ① 第一步先放主件，把附件先存着；直到主件放完，再去放附件；
    ② 循环的放；比如 主件+附件1+附件2=(主件+附件1)+附件2;也就是在前个物品基础之上再加上附件2
    */
    for (int i = 1; i <= n; i++)
        for (auto c : b[i]) { // 遍历每个附件
            int w = c.w, v = c.v;
            int sz = a[i].size();
            for (int j = 0; j < sz; j++)
                a[i].push_back({a[i][j].w + w, a[i][j].v + v}); // 把扩展出来的组放在尾巴上
        }

    // 分组背包模板
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= 0; j--)
            for (int k = 0; k < a[i].size(); k++) // 注意：这里k是从0开始，因为vector的特点决定
                if (j >= a[i][k].w)
                    f[j] = max(f[j], f[j - a[i][k].w] + a[i][k].v);
    // 输出
    printf("%d\n", f[m]);
    return 0;
}