7.7 KiB
一、题目描述
有 N 个物品和一个容量是 V 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示:
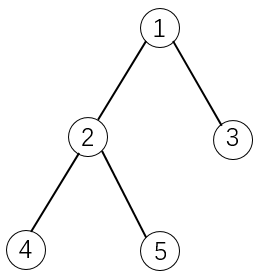
如果选择物品5,则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。
每件物品的编号是 i,体积是 v_i,价值是 w_i,依赖的父节点编号是 p_i。物品的下标范围是 1…N。
求解将哪些物品装入背包,可使 物品总体积不超过背包容量,且 总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,V,用空格隔开,分别表示物品个数和背包容量。
接下来有 N 行数据,每行数据表示一个物品。
第 i 行有三个整数 v_i,w_i,p_i,用空格隔开,分别表示物品的体积、价值和依赖的物品编号。
如果 p_i=−1,表示根节点。 数据保证所有物品构成一棵树。
输出格式 输出一个整数,表示最大价值。
数据范围
1≤N,V≤100
1≤v_i,w_i≤100
父节点编号范围:
- 内部结点:
1≤p_i≤N; - 根节点
p_i=−1;
输入样例
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2
输出样例:
11
二、题目解析
这是一道 背包DP 的 变种题目
根据题设的 拓扑结构 可以观察出每个 物品 的关系构成了一棵 树
而以往的 背包DP 每个 物品 关系是 任意的(但我们一般视为 线性的)
所以,这题沿用 背包DP 的话,要从原来的 线性DP 改成 树形DP 即可
然后思考 树形DP 的 状态转移
先比较一下以往 线性背包DP 的 状态转移,第 i 件 物品 只会依赖第 i−1 件 物品 的状态
如果本题我们也采用该种 状态依赖关系 的话,对于节点 i,我们需要枚举他所有子节点的组合 2^k 种可能
再枚举 体积,最坏时间复杂度 可能会达到 O(N×2^N×V)(所有子节点都依赖根节点)最终毫无疑问会 TLE
因此我们需要换一种思考方式,那就是枚举每个 状态 分给各个子节点 的 体积
这样 时间复杂度 就是 O(N×V×V)
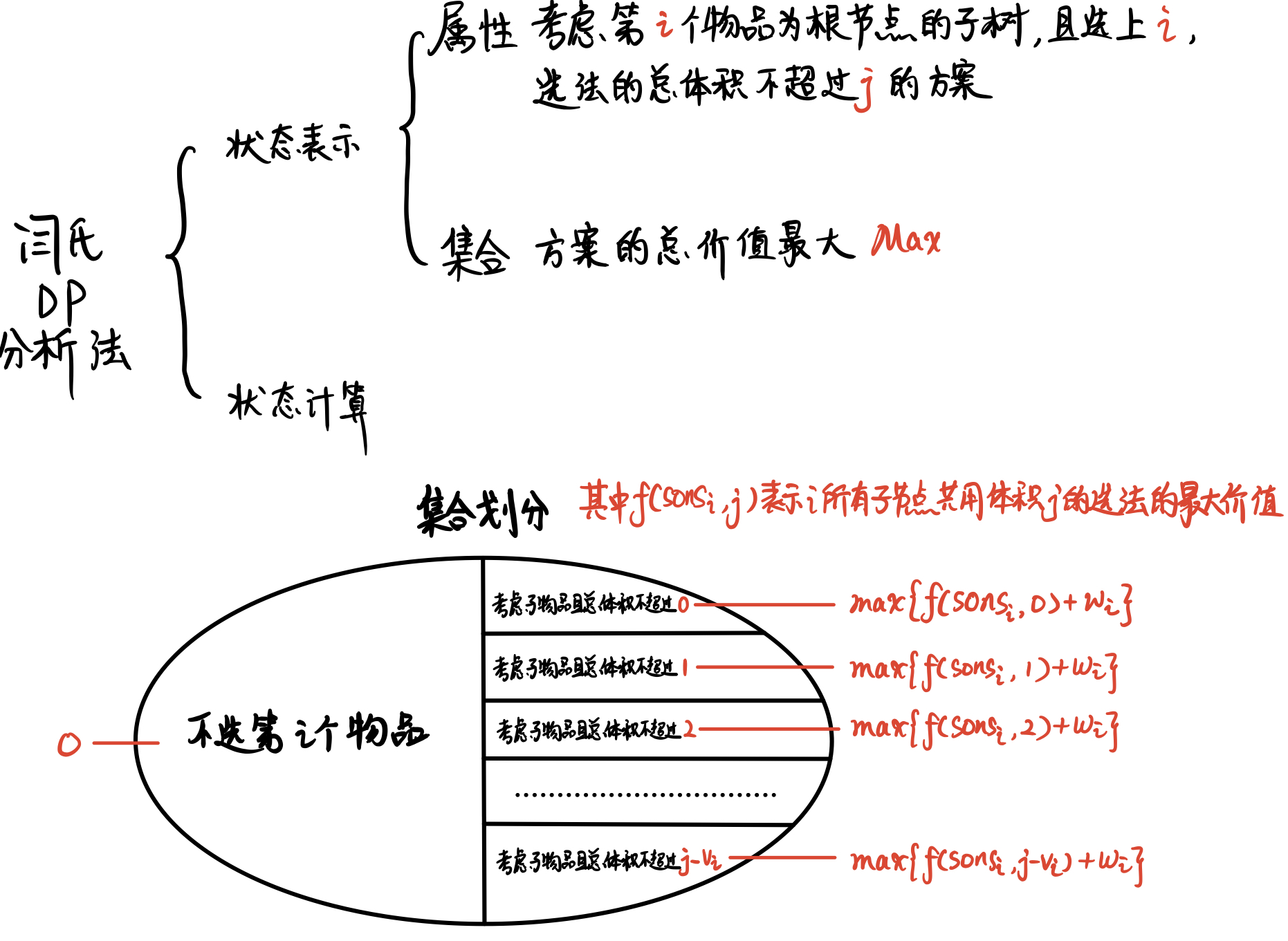
状态表示
集合
f[u][i][j] 以u为根,在前i个子树中选择,最大体积不超过j的所有方案
解释 ①
i可以等于0,描述只要了u节点,没有要u的下级任何一个儿子子树。 ② 需要满足条件j>=v[u],原因是如果你连u节点都装不下,那就更别提装下u及它的若干个儿子树了
属性
max(价值)
1、三维
#include <bits/stdc++.h>
using namespace std;
const int N = 110, M = N << 1;
int v[N], w[N];
int n, m, root;
// f[u][i][j] 以u为根,在前i个子树中(组)选择,最大体积不超过j的所有方案
// 属性:max价值
int f[N][N][N];
// 链式前向星
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// u:以u为根的树
// 返回值:以u为根的树,一级子树son的个数
int dfs(int u) {
/*
① 以u为根的树,如果现在剩余体积j>=v[u], 最起码可以把u装下,能获取到w[u]的价值
如果你想研究一下以u为根的子树最多可以获得多大价值,那u节点是必须装下来,否则后续子树根本没机会讨论
*/
for (int j = v[u]; j <= m; j++) f[u][0][j] = w[u];
// ② 考虑u的每个子树
int s = 0;
for (int i = h[u]; ~i; i = ne[i]) { // 枚举u的每个子节点
s++; // 前s个子树
int son = e[i]; // 在链式前向星中,这是几号节点
int c = dfs(
son); // 对子节点son,把它的f[son][c][k]信息填充完整,返回son子树的一级结点个数
/*
目标:填充f[u][i][j],
i:
1~dfs(u)的每个值,dfs(u)返回的是u的下级节点个数,也就是一级子树个数,0上面讨论过了,不用再讨论
j: 枚举每一个u子树的合法空间j
k:给定j这么大的空间,那么为son这棵子树留多大空间,k∈
[0,j-v[u]],son子树可以贡献的最大价值依定义就是f[son][c][k] f[u][s -
1][j -
k]:在处理s个子树前,前s-1个都已经填充完毕,可以依赖。由于son占了k个空间,那么前序依赖就是f[u][s-1][j-k]
*/
for (int j = v[u]; j <= m; j++)
for (int k = 0; k <= j - v[u]; k++)
f[u][s][j] = max(f[u][s][j], f[u][s - 1][j - k] + f[son][c][k]);
}
return s; // 返回u有多少个子结点
}
int main() {
// 初始化链式前向星
memset(h, -1, sizeof h);
cin >> n >> m; // 物品个数和背包容量
for (int i = 1; i <= n; i++) { // n个物品
int p;
cin >> v[i] >> w[i] >> p; // 体积、价值、父亲
if (p == -1)
root = i; // 对一棵树而言,根是最重要的
else
add(p, i); // 从父亲向儿子建边,一般树都是从上到下建边
}
int s = dfs(root); // 从根节点开始遍历,填充DP Table,返回值是root有几个子树
/*
Q:为什么需要dfs返回root有多少个子树呢?
A:DP问题,一般的答案都在状态转移方程上。比如f[u][i][j]表示以u为根的树中,在前i个儿子中去找,在体积不超过j的情况下,最大的价值是多少。
我们可以看出,最终的答案就是f[root][root的儿子总数][m]
这样看来,计算返回出root的儿子总数就是合情合理了
*/
printf("%d\n", f[root][s][m]);
return 0;
}
2、二维
这就是一个类似于01背包降维的办法,采用倒序计算,可以防止依赖先更新。
#include <bits/stdc++.h>
using namespace std;
const int N = 110, M = N << 1;
int v[N], w[N];
int n, m, root;
int f[N][N];
// 链式前向星
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u) {
for (int j = w[u]; j <= m; j++) f[u][j] = v[u];
for (int i = h[u]; ~i; i = ne[i]) {
int son = e[i];
dfs(son);
for (int j = m; j >= w[u]; j--)
for (int k = 0; k <= j - w[u]; k++)
f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
}
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int p;
cin >> w[i] >> v[i] >> p;
if (p == -1)
root = i;
else
add(p, i);
}
dfs(root);
printf("%d\n", f[root][m]);
return 0;
}