python

4.0 KiB

Raw Permalink Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

多叉树转二叉树-有依赖的背包问题解法

一、多叉树的定义

多叉树即为子结点有任意个的树，而在转换时所涉及的多叉树是一棵有序的多叉树，也就是其子结点的顺序是不能够随便交换的。

二、二叉树的定义

二叉树是每个结点最多有两个后继，且子树有左右之分（次序不能任意颠倒）。

三、多叉树转二叉树的作用

在用数组等表示或保存多叉树时，会浪费存储的空间
由于树中每个结点的度各不相同，在搜索过程中会比较困难。
二叉树相对于多叉树便有了这些方面的优势，即能够节省存储空间，又能使搜索变得简便快捷。

因此可以通过将多叉树转换成为二叉树从而实现优化。

四、转换规则

将一棵多叉树转换成二叉树，我们遵循的原则是： 左儿子，右兄弟。

算法描述

将多叉树的第一个儿子结点作为二叉树的左结点，将其兄弟结点作为二叉树的右结点。

假设多叉树为T，新转化的二叉树为K

T中的结点与K中的结点一一对应。
T中的某个结点N的第一个子结点为N_1，则K中N_1为N的左儿子结点
T中的某个结点N的第i个子结点记为N_i(除第一个子结点)，则K中N_i为N_{i-1}的右儿子结点(N_2为N_1的右儿子结点，N_3为N_2的右儿子结点)

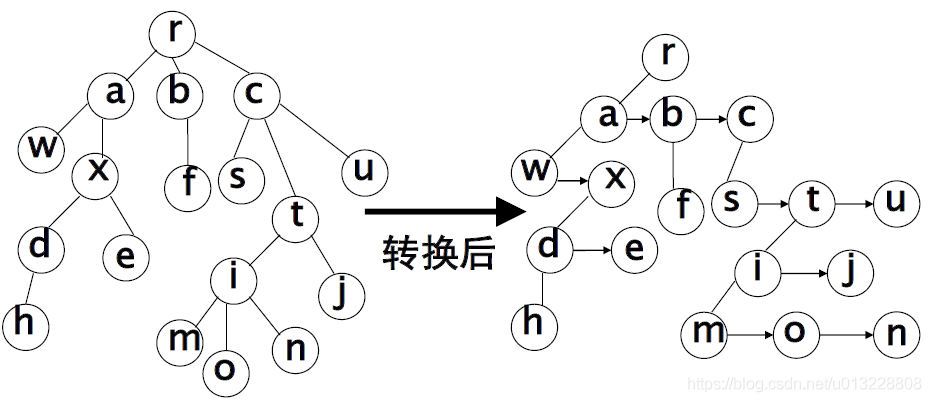
五、转换示意图

六、具体实现代码

AcWing 10. 有依赖的背包问题

#include <bits/stdc++.h>

using namespace std;
const int N = 105;
int n;          //物品个数
int m;          //背包容量
int v[N];       //物品的体积
int w[N];       //物品的价值
int p;          //依赖的物品编号
int root;       //根节点

//多叉树转二叉树
int l[N], r[N]; //左儿子，右兄弟
int son[N];     //记录i的目前输入的最后一个儿子是谁，为了后面再有其它儿子加入时，放到最后一个儿子的右子树上

/*i表示结点，j表示体积,f[i][j]表示i及其兄弟结点组合不超过体积j的最大价值。由于根结点没有兄弟结点，故f[root][v]
表示体积不超过v的最大价值*/
int f[N][N];

/**
 * 功能：计算以i及其兄弟结点组合，体积不超过j的最大价值
 * @param i 根
 * @param j 体积
 * @return 最大价值
 */
int dfs(int i, int j) {
    if (i == 0 || j == 0) return 0; //递归出口,i=0:比如一个结点没有左儿子，默认就是i=0;
    if (f[i][j]) return f[i][j];    //记忆化
    //右子树,也就是兄弟们的最大值
    f[i][j] = dfs(r[i], j);
    //计算以自己为根的子树最大值(需要预留出v[i]的空间出来)并PK兄弟们的最大值
    for (int k = 0; k <= j - v[i]; k++)//遍历所有可能的空间
        //如果要了i结点，那么结果可能来自三方面：左子树，右子树，自己的w[i]
        f[i][j] = max(f[i][j], dfs(r[i], k) + dfs(l[i], j - v[i] - k) + w[i]);
    //返回最大值
    return f[i][j];
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        //体积，价值，依赖的物品编号
        cin >> v[i] >> w[i] >> p;
        //将录入的多叉树转为二叉树，方便查找
        if (p == -1) root = i;//记录根节点
        else {
            if (son[p] == 0) l[p] = i; //p还没有录入过儿子，那么记录p的左儿子=i
                //如果p录入过儿子，那么需要找出它最后一个儿子是son[p],
                // 将i记录到最后一个儿子的右结点上r[son[p]]=i
            else r[son[p]] = i;
            son[p] = i;                //修改p的最后一个儿子为i
        }
    }
    //深搜
    cout << dfs(root, m) << endl;
    return 0;
}

4.0 KiB Raw Permalink Blame History Unescape Escape