python/TangDou/AcWing/BalanceTree/253.md

##AcWing 253. 普通平衡树

一、题目描述

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

• 1 插入数值 x。
• 2 删除数值 x(若有多个相同的数，应只删除一个)。
• 3 查询数值 x 的排名(若有多个相同的数，应输出最小的排名)。
• 4 查询排名为 x 的数值。
• 5 求数值 x 的前驱(前驱定义为小于 x 的最大的数)。
• 6 求数值 x 的后继(后继定义为大于 x 的最小的数)。

注意： 数据保证查询的结果一定存在。

输入格式 第一行为 n，表示操作的个数。

接下来 n 行每行有两个数 opt 和 x，opt 表示操作的序号(1≤opt≤6)。

输出格式 对于操作 3,4,5,6 每行输出一个数，表示对应答案。

数据范围 1≤n≤100000,所有数均在 −10^7 到 10^7 内。

输入样例：

8
1 10
1 20
1 30
3 20
4 2
2 10
5 25
6 -1

输出样例：

2
20
20
20

二、STL+vector

和我一起大声读：STL大法好！645 ms,比Treap平衡树慢一倍左右。

#include <cstdio>
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;

int n;
vector<int> a;

int main() {
    //加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    cin >> n;
    int op, x;
    while (n--) {
        cin >> op >> x;
        if (op == 1)
            a.insert(lower_bound(a.begin(), a.end(), x), x); //插入数值x
        else if (op == 2)
            a.erase(lower_bound(a.begin(), a.end(), x)); //删除数值x
        else if (op == 3)
            printf("%d\n", lower_bound(a.begin(), a.end(), x) - a.begin() + 1); //查询数值 x 的排名
        else if (op == 4)
            printf("%d\n", a[x - 1]); //查询排名为 x 的数值
        else if (op == 5)
            printf("%d\n", *--lower_bound(a.begin(), a.end(), x)); //求数值 x 的前驱
        else if (op == 6)
            printf("%d\n", *upper_bound(a.begin(), a.end(), x)); //求数值 x 的后继
    }
    return 0;
}

三、普通平衡树Treap

本题是一道普通平衡树Treap的引入模板题，是想让我们了解并开始学习平衡树的，用STL水过，一来可以让大家更好的学习STL,二来是没有背下来普通平衡树、FHQ树、Splay之前，有一技傍身，废话少说，开始操练：

Treap 指 Tree + heap，又叫作 树堆，同时满足二叉搜索树和堆两种性质。二叉搜索树满足中序有序性，输入序列不同，创建的二叉搜索树也不同，在 最坏的情况 下（只有左子树或只有右子树）会退化为 线性。例如输入1 2 3 4 5，创建的二叉搜索树如下图所示。

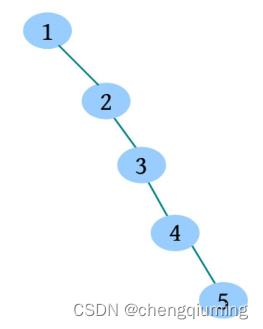
二叉搜索树 BST 的插入、查找、删除等效率与树高成正比，因此在创建二叉搜索树时 要尽可能通过调平衡压缩树高。平衡树有很多种，例如 AVL 树、伸展树、SBT、红黑树等，这些调平衡的方法相对复杂。

若一个二叉搜索树插入节点的顺序是随机的，则得到的二叉搜索树在大多数情况下是平衡的，即使存在一些极端情况，这种情况发生的概率也很小，因此 以随机顺序创建的二叉搜索树，其期望高度为logn。这是有数学定理证明过的，水平所限，不再详细论述。所以，可以将输入数据随机打乱，再创建二叉搜索树，但我们有时并不能事前得知所有待插入的节点，而Treap可以有效解决该问题。

在 Treap 的构建过程中，插入节点时会给每个节点都 附加一个随机数作为优先级，该优先级满足堆的性质（最大堆或最小堆均可，这里以 最大堆为例，根的优先级大于左右子节点），数值满足二叉搜索树性质（中序有序性，左子树小于根，右子树大于根）。

BST的中序遍历 投影法则

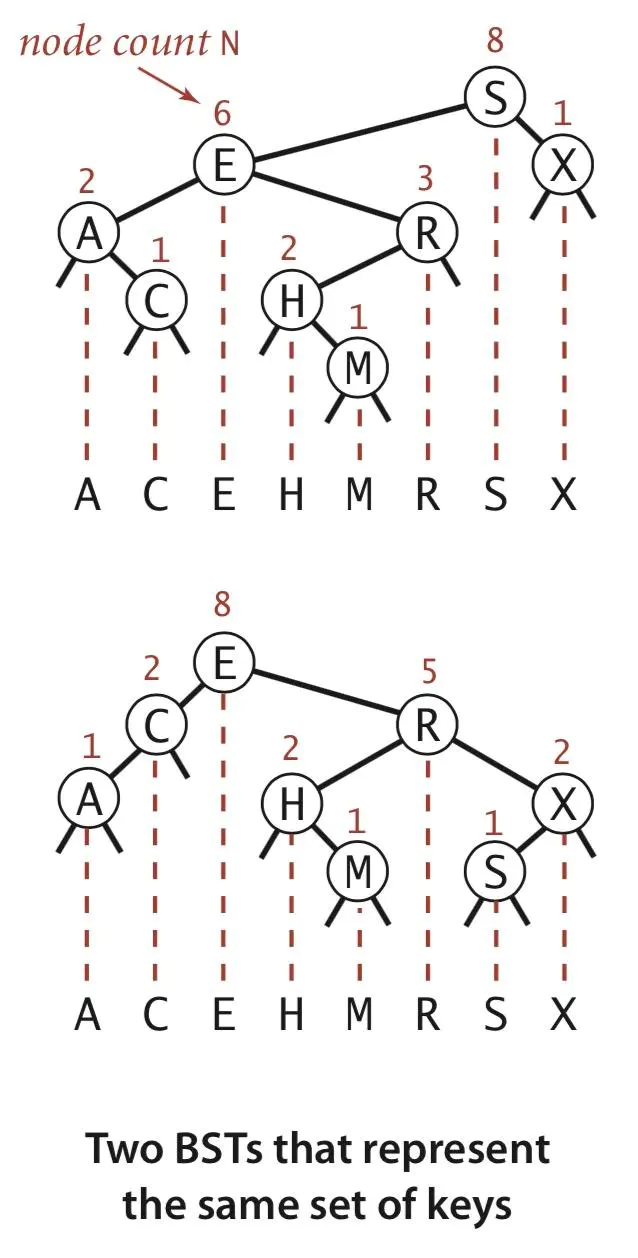
同样的中序遍历输出其实在真正的存储时，是不一样的形态。我们只要维持住中序遍历的次序不变，结合大顶堆的随机值在上的特点，就可以得到一个 矮粗胖 的平衡树，获取最好的性能。

构建过程

输入 6 4 9 7 2，构建 Treap。首先给每个节点都附加一个随机数作为优先级，根据 输入数据 和 附加随机数，构建的 Treap 如下图所示。

右旋和左旋

Treap 需要两种神操作，通过两个神操作，才能保证平衡树不是一条链，而是又矮又胖，这两个神操作是：右旋和左旋

右旋（zig） 节点 p 右旋时，会携带自己的右子树，向右旋转到 q 的右子树位置，q 的右子树被抛弃，此时 p 右旋后左子树正好空闲，将 q 的右子树放在 p 的左子树位置，旋转后的树根为 q 。

动画演示：

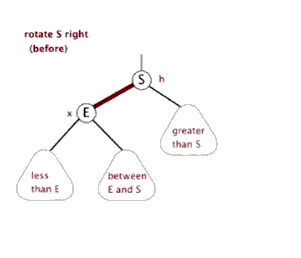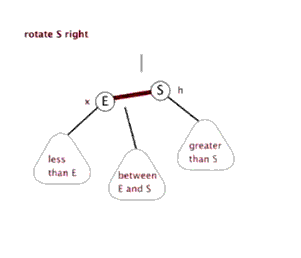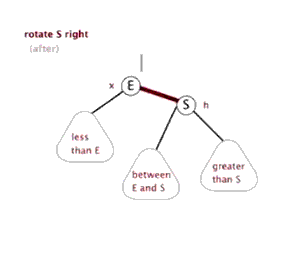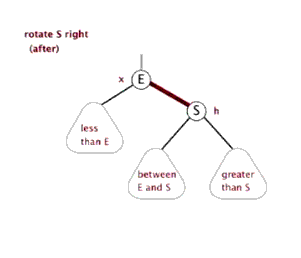
左旋（zag） 节点 p 左旋时，携带自己的左子树，向左旋转到 q 的左子树位置，q 的左子树被抛弃，此时 p 左旋后右子树正好空闲，将 q 的左子树放在 p 的右子树位置，旋转后的树根为 q 。

动画演示：

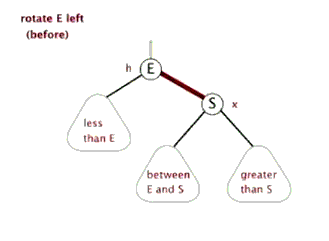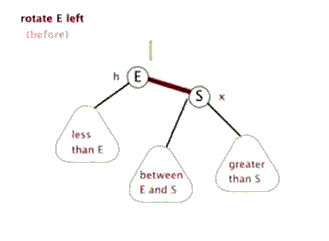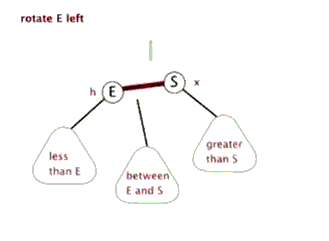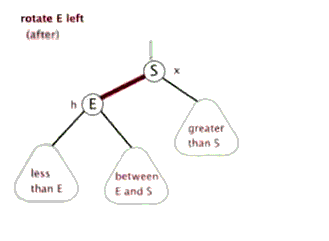
插入 insert

Treap 的插入操作和二叉搜索树一样，首先根据有序性找到插入的位置，然后创建新节点插入该位置。创建新节点时，会给该节点附加一个随机数作为优先级，自底向上检查 该优先级是否满足堆性质，若不满足，则需要右旋或左旋，使其满足堆性质。

算法步骤:

• ① 从根节点 p 开始，若 p 为空，则创建新节点，将待插入元素 key 存入新节点，并给新节点附加一个随机数val作为优先级

• ② 若 key 等于 tr[p].key，则 tr[p].cnt++

• ③ 若 key 小于 tr[p].key，则在 p 的左子树中递归插入。回溯时做旋转调整，若 tr[p].val < tr[p[l]].val ，则 p 右旋

• ④ 若 key 大于 tr[p].key，则在 p 的右子树中递归插入。回溯时做旋转调整，若 tr[p].val < tr[p.r].val ，则 p 左旋

一个树堆如下图所示，在该树堆中插入元素 8，插入过程如下:

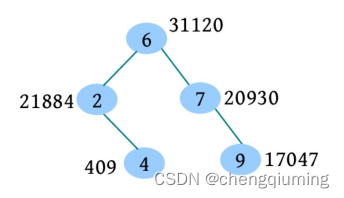
（1）根据二叉搜索树的插入操作，将 8 插入 9 的左子节点位置，假设 8 的随机数优先级为 25016。

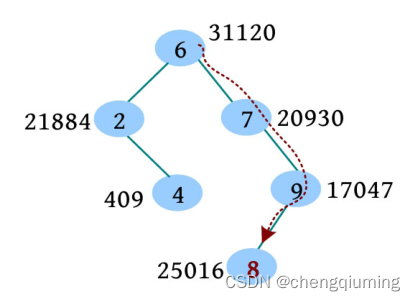
（2）回溯时，判断是否需要旋转，9 的优先级比其左子节点小，因此 9 节点右旋。

（3）继续向上判断，7 的优先级比 7 的右子节点小，因此7节点左旋。

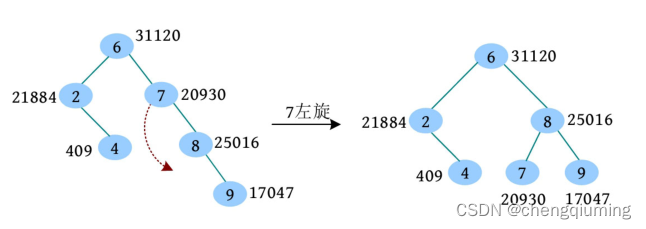
（4）继续向上判断，6 的优先级不比 6 的左右子节点小，满足最大堆性质，无须调整，已向上判断到树根，算法停止。

删除 remove

Treap 的删除操作 ：找到待删除的节点，将该节点向优先级大的子节点旋转，一直旋转到叶子，直接删除叶子即可。

算法步骤

• 从根节点 p 开始，若待删除元素 key 等于 tr[p].key，则：

  • 若 p 只有左子树或只有右子树，则令其子树子承父业代替 p ，返回；
  • 若 tr[p.l].val > tr[p.r].val ，则 p 右旋，继续在 p 的 右子树中递归 删除
  • 若 tr[p.l].val < tr[p.r].val ，则 p 左旋，继续在 p 的 左子树中递归 删除

• 若 key < tr[p].key，则在 p 的 左子树中递归 删除

• 若 key > tr[p].key，则在 p 的 右子树中递归 删除

在上面的树堆中删除元素 8，删除过程如下:

（1）根据二叉搜索树的删除操作，首先找到 8 的位置，8 的右子节点优先级大，8 左旋。

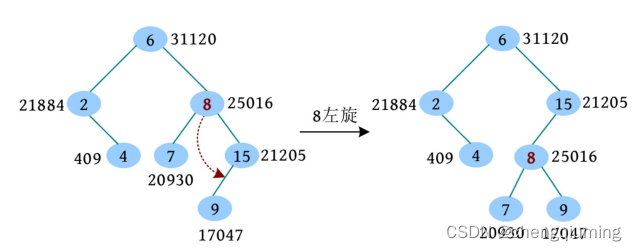
（2）接着判断，8 的左子节点优先级大，8 右旋。

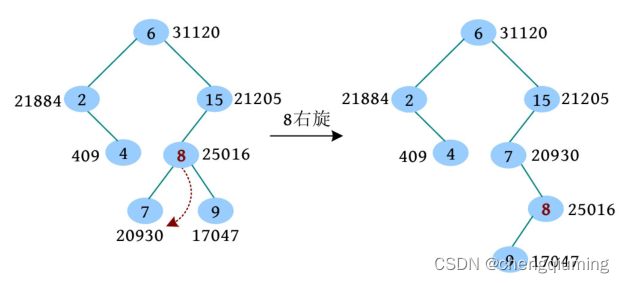
（3）此时 8 只有一个左子树，左子树子承父业代替它

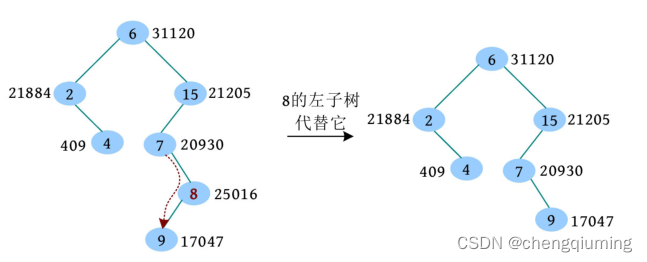
前驱 get\_prev

在 Treap 中求一个节点 key 的前驱时，首先从树根开始，若当前节点的值小于 key，则用 res 暂存该节点的值，在当前节点的右子树中寻找，否则在当前节点的左子树中寻找，直到当前节点为空，返回 res，即为 key 的前驱。

后继 get\_next

在 Treap 中求一个节点 key 的后继时，首先从树根开始，若当前节点的值大于 key，则用 res 暂存该节点的值，在当前节点的左子树中寻找，否则在当前节点的右子树中寻找，直到当前节点为空，返回 res，即为 key 的后继。

三、实现代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010, INF = 1e8;

int n;
struct Node {
    int l, r;      // 左右儿子节点号
    int key, val;  // BST中的真实值，堆中随机值
    int cnt, size; // 当前数字个数,小于等于当前数字的数字个数总和
} tr[N];

int root, idx;

void pushup(int p) {
    tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + tr[p].cnt; // BST左子树数字个数+右子树数字个数+自己数字个数
}

int get_node(int key) {
    tr[++idx].key = key;  //填充 BST的值
    tr[idx].val = rand(); //堆中的随机值
    tr[idx].cnt = tr[idx].size = 1;
    return idx;
}

//右旋
void zig(int &p) {
    int q = tr[p].l;
    tr[p].l = tr[q].r;
    tr[q].r = p;
    p = q;
    pushup(tr[p].r), pushup(p);
}

//左旋
void zag(int &p) {
    int q = tr[p].r;
    tr[p].r = tr[q].l;
    tr[q].l = p;
    p = q;
    pushup(tr[p].l), pushup(p);
}

void build() {
    get_node(-INF), get_node(INF);
    root = 1, tr[1].r = 2;
    pushup(root);
    if (tr[1].val < tr[2].val) zag(root);
}

void insert(int &p, int key) {
    if (!p)
        p = get_node(key);
    else if (tr[p].key == key)
        tr[p].cnt++;
    else if (tr[p].key > key) {
        insert(tr[p].l, key);                    //往左边插入
        if (tr[tr[p].l].val > tr[p].val) zig(p); //左儿子大，右旋
    } else {
        insert(tr[p].r, key);                    //往右边插入
        if (tr[tr[p].r].val > tr[p].val) zag(p); //右儿子大，左旋
    }
    pushup(p);
}

void remove(int &p, int key) {
    if (!p) return; //如果发现p==0, 就是没找着

    if (tr[p].key == key) { //如果找着了
        if (tr[p].cnt > 1)  //并且不止1个，这个就简单了，去掉一个就行了,记得 pushup
            tr[p].cnt--;
        else if (tr[p].l || tr[p].r) {                           //如果只有1个，并且，有左儿子或右儿子，这时不能直接删除掉，需要处理一下
            if (!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val) { //如果没有右儿子，或者是左儿子的随机值大于右儿子随机值，右旋
                zig(p);                                          //右旋后，此值向右运动，继续递归右子树处理
                remove(tr[p].r, key);
            } else {
                zag(p); //左旋，此值向左运动，继续递归向左子树处理
                remove(tr[p].l, key);
            }
        } else
            p = 0;              //左右都没有子树，直接标识为删除
    } else if (tr[p].key > key) //如果在左
        remove(tr[p].l, key);
    else
        remove(tr[p].r, key); //如果在右

    //向上更新统计信息
    pushup(p);
}

int get_rank(int p, int key) { // 通过数值找排名
    if (!p) return 0; // 本题中不会发生此情况
    if (tr[p].key == key) return tr[tr[p].l].size + 1;
    if (tr[p].key > key) return get_rank(tr[p].l, key);
    return tr[tr[p].l].size + tr[p].cnt + get_rank(tr[p].r, key);
}

int get_key(int p, int rank) { // 通过排名找数值
    if (!p) return INF; // 本题中不会发生此情况
    if (tr[tr[p].l].size >= rank) return get_key(tr[p].l, rank);
    if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key;
    return get_key(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt);
}

int get_prev(int p, int key) { // 找到严格小于key的最大数
    if (!p) return -INF;
    if (tr[p].key >= key) return get_prev(tr[p].l, key);
    return max(tr[p].key, get_prev(tr[p].r, key)); //当前位置可能成为答案
}

int get_next(int p, int key) { // 找到严格大于key的最小数
    if (!p) return INF;
    if (tr[p].key <= key) return get_next(tr[p].r, key);
    return min(tr[p].key, get_next(tr[p].l, key));
}

int main() {
    //加快读入
    ios::sync_with_stdio(false), cin.tie(0);

    build();

    cin >> n;
    while (n--) {
        int op, x;
        cin >> op >> x;
        if (op == 1)
            insert(root, x);
        else if (op == 2)
            remove(root, x);
        else if (op == 3)
            printf("%d\n", get_rank(root, x) - 1);
        else if (op == 4)
            printf("%d\n", get_key(root, x + 1));
        else if (op == 5)
            printf("%d\n", get_prev(root, x));
        else
            printf("%d\n", get_next(root, x));
    }
    return 0;
}

四、fhq 树堆

FHQ Treap,以下简写为fhq,是一种treap(树堆)的变体,功能比treap强大,代码比splay好写,易于理解,常数稍大.

fhq 不需要 通过一般平衡树的 左右旋转 来保持平衡,而是通过 分裂split 和 合并merge 来实现操作。

结构

以结构体作为树的每一个节点,存储:

• ① 左子树位置
• ② 右子树的位置
• ③ 权值key
• ④ 堆中随机索引val
• ⑤ 子树大小.一般子树大小用于查排名和查值

root是树根编号,idx是点的编号.

struct Node {
    int l, r;       //  左右子树编号
    int key, val;   //  key权 val堆权
    int size;       //  子树大小 
} tr[N];
int root, idx;

fhq和treap一样满足treap的性质,也就是 既是BST,又是 随机权值的堆.

至于为什么满足堆的性质的BST就能平衡,有如下定理保证:

一颗有n个不同关键字随机构建的BST的期望高度为logn.

随机堆的权值正是模拟了随机构建BST,所以treap是平衡的,同理fhq也平衡.

创建节点和更新子树大小

 int get_node(int key) {
    tr[++idx].key = key;
    tr[idx].val = rnd();
    tr[idx].size = 1;
    return idx;
}
void pushup(int p) {
    tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + 1;
}

子树大小由两侧子树和根节点更新.rnd()为随机值产生函数。

首先fhq-treap是一个二叉搜索树(BST)，它的每个节点有两个主要信息：key和val，key是我们fhq-treap要维护的键值，而val是随机生成的(rand()),key信息主要用于我们对于题目信息的处理，而val则是用于维持fhq-treap在结构上满足期望高度为O(logn)的。fhq-treap 除了要满足关于key的BST性质之外，还需满足关于val的 小根堆 性质。就是说，对于任意fhq-treap中的节点 i :

• 其左子树上的所有节点的key 小于等于 i 节点的key值，i 节点所有右子树上所有节点的key 大于等于 i 节点的key值

• 对于任意节点 i ，其左、右儿子的val值 大于等于 i 的val值(满足 小根堆 的性质)

要牢牢记住这两点的区别，否则会像我一样搞混，然后写代码的时候狂 WA，。下面给出一颗fhq-treap：

上图就是一颗fhq-treap，其中每个节点中的数字为val，每个节点下方的数字为当前节点的key。可以发现一颗fhq-treap中序遍历后得到的序列是单调递增。 这里，我们要引入fhq-treap的两个基本操作：split和merge， 其中split是分离操作，merge是合并操作，下面我们来一一阐明：

1. split操作

通常情况下，split 用于分离一颗fhq-treap，对于一个元素 x ，我们会将这棵fhq-treap分裂为左右两棵树，左树上每个节点的key值都小于等于(<=)x , 而右树上的所有节点的key值都大于 x ；下面给出代码：

//将以p为根的平衡树进行分裂，小于等于key的都放到以x为根的子树中，大于key放到以y为根的子树中
void split(int p, int key, int &x, int &y) {
    if (!p) { //当前节点为空
        x = y = 0;
        return;
    }
    if (tr[p].key <= key)
        x = p, split(tr[p].r, key, tr[p].r, y); // x确定了，左边确定了，但右边未确定，需要继续递归探索
    else
        y = p, split(tr[p].l, key, x, tr[p].l); // y确定了，右边确定了，但左边未确定，需要继续递归探索

    pushup(p); //更新统计信息
}

以上代码如果学过线段树的话会好理解的多，本蒟蒻也建议先去熟练掌握线段树再来学习fhq-treap，这样会轻松很多。下面我们来模拟这个过程—— 本蒟蒻就是开始没有自己去模拟，导致一直不是很理解fhq-treap的实现方式。

对于上图，假如我们要将其分离为小于等于18和大于18两个部分：

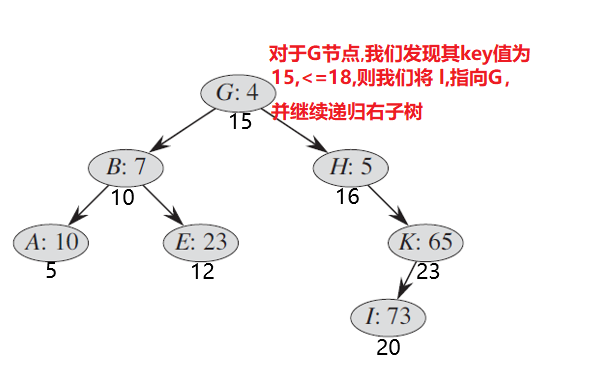
经过此役，x的指向已经很清楚了，就是p=G,因为G左侧的所有数，都会比G小，所以左子树的范围也就相应继承下来了:tr[p].l不需要动，但x的右边界不没有确定，因为18到底应该在右子树的哪个位置割开呢？还需要继续研究，继续递归解决。

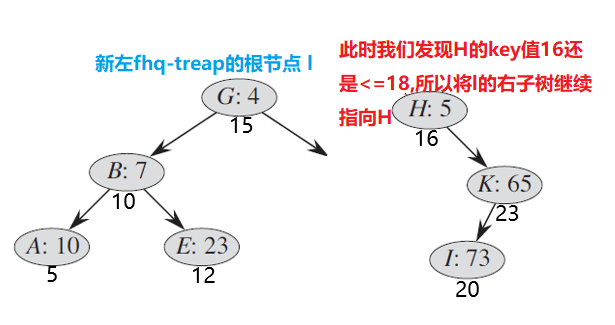
经过此役，x 的右边界还在不断的修改，不断的向右逼近。

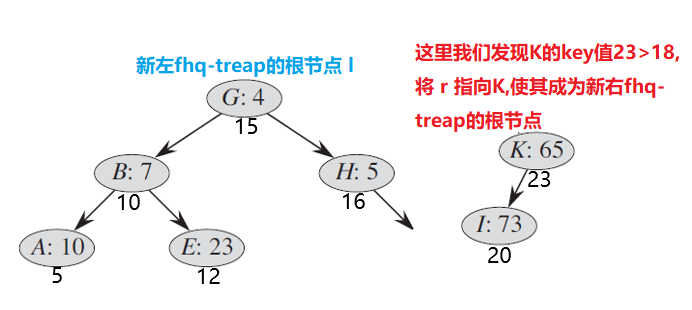
经过此役，出现了第一个大于key的点，那么此点做为一个有代表性的点，被设置为y。同时，x的右边界，y的左边界依然不明，需要继续递归查找。分裂K节点的左子树，由于I节点的权值20>18，所以我们将 I 节点归入右fhq-treap，接下来我们会碰到空节点，递归将会跳出，这时，我们就能得到左右两棵fhq-treap了：

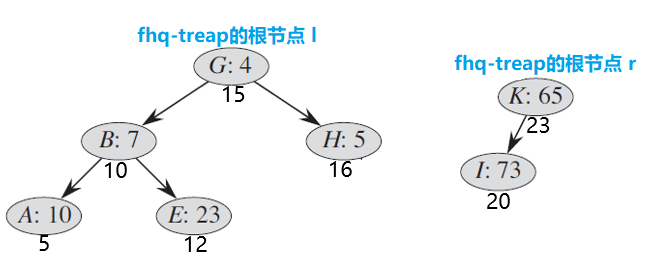
以上就是fhq-treap的基本操作之一split操作的全部过程了 。

2. merge 操作 这是一个合并操作，但它也不能随便合并，如果要合并两棵fhq-treap，那么它们可以进行合并当且仅当左fhq-treap上所有节点的key值都小于等于右fhq-treap中的最小key值(也就是左树小于等于右树)或两棵树中有空树。 这个性质很重要，为根据val合并两棵树做好的前提，保证了BST结构不会因合并而被破坏。 合并时，我们会根据左右两棵树的根节点的val值大小进行合并，大家先看一下代码：

//将以x，y为根的两个子树合并成一棵树.要求x子树中所有key必须小于等于y子树中所有key
int merge(int x, int y) {
    if (!x || !y) return x + y; //如果x或者y有一个是空了，那么返回另一个即可

    int p;                       //根,返回值
    if (tr[x].val > tr[y].val) { // x.key<y.key,并且, tr[x].val > tr[y].val, x在y的左上，此时理解为大根堆,y向x的右下角合并
        p = x;
        tr[x].r = merge(tr[x].r, y);
    } else {
        p = y;
        tr[y].l = merge(x, tr[y].l); //复读机
    }

    pushup(p); //更新统计信息
    return p;
}

还是一样，画图好理解：

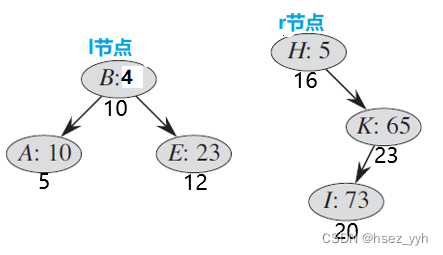
以上是两棵要合并的fhq-treap

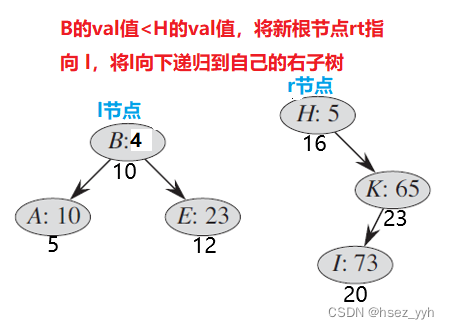
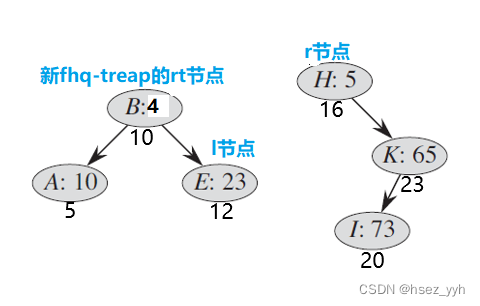
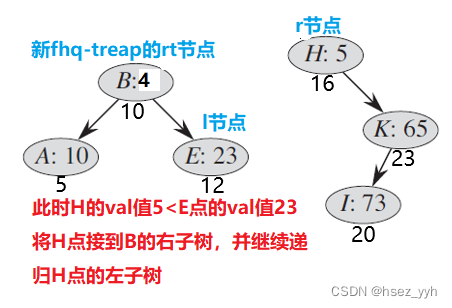
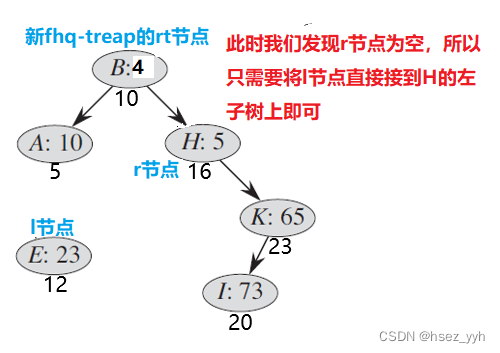
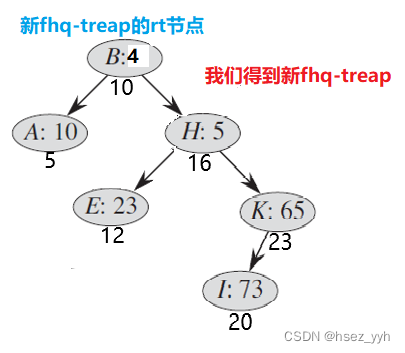
以上就是fhq-treap合并的全部过程了。

六、实现代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>

//普通Treap  316 ms
// FHQ Treap 433 ms
//两者基本在一个数量级上，常数略大

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 1e5 + 10;

struct Node {
    int l, r; //左右儿子的节点号
    int key;  // BST中的真实值
    int val;  //堆中随机值,用于防止链条化
    int size; //小于等于 key的数字个数，用于计算rank等属性
} tr[N];

int root, idx; //用于动态开点，配合tr记录FHQ Treap使用
int x, y, z;   //本题用的三个临时顶点号

void pushup(int p) {
    tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + 1; //合并信息
}

int get_node(int key) {   //创建一个新节点
    tr[++idx].key = key;  //创建一个新点，值为key
    tr[idx].val = rand(); //随机一个堆中索引号
    tr[idx].size = 1;     //新点，所以小于等于它的个数为1个，只有自己
    return idx;           //返回点号
}

//将以p为根的平衡树进行分裂，小于等于key的都放到以x为根的子树中，大于key放到以y为根的子树中
void split(int p, int key, int &x, int &y) {
    if (!p) { //当前节点为空
        x = y = 0;
        return;
    }
    if (tr[p].key <= key)
        x = p, split(tr[p].r, key, tr[p].r, y); // x确定了，左边确定了，但右边未确定，需要继续递归探索
    else
        y = p, split(tr[p].l, key, x, tr[p].l); // y确定了，右边确定了，但左边未确定，需要继续递归探索

    pushup(p); //更新统计信息
}

//将以x，y为根的两个子树合并成一棵树.要求x子树中所有key必须小于等于y子树中所有key
int merge(int x, int y) {
    if (!x || !y) return x + y; //如果x或者y有一个是空了，那么返回另一个即可

    int p;                       //根,返回值
    if (tr[x].val > tr[y].val) { // x.key<y.key,并且, tr[x].val > tr[y].val, x在y的左上，此时理解为大根堆,y向x的右下角合并
        p = x;
        tr[x].r = merge(tr[x].r, y);
    } else {
        p = y;
        tr[y].l = merge(x, tr[y].l); //复读机
    }

    pushup(p); //更新统计信息
    return p;
}

void insert(int key) {
    split(root, key, x, y);                   //按k分割
    root = merge(merge(x, get_node(key)), y); //在x与key节点合并,再与key合并
}

void remove(int key) {
    split(root, key, x, z);
    split(x, key - 1, x, y);
    // x<=key ,再分x <= key - 1,y就是=key的树
    y = merge(tr[y].l, tr[y].r);  //删除y点(根)
    root = merge(merge(x, y), z); //合并x,y,z
}

int get_rank(int key) {         //按值查排名
    split(root, key - 1, x, y); //按key-1分割,x子树大小+1就是排名
    int rnk = tr[x].size + 1;   //储存x的大小+1
    root = merge(x, y);
    return rnk;
}

int get_key(int rnk) { //按排名查值
    int p = root;
    while (p) {
        if (tr[tr[p].l].size + 1 == rnk)
            break; //找到排名了
        else if (tr[tr[p].l].size >= rnk)
            p = tr[p].l; //当前size>=rank,去左子树
        else {
            //去右子树中找rank -= 左子树大小+1(根)的排名
            rnk -= tr[tr[p].l].size + 1;
            p = tr[p].r;
        }
    }
    return tr[p].key;
}

//返回<key的最大数
int get_prev(int key) {
    split(root, key - 1, x, y); //按key-1分,x最右节点就是前驱
    int p = x;
    while (tr[p].r) p = tr[p].r; //向右走
    int res = tr[p].key;
    root = merge(x, y);
    return res;
}

//返回>key的最小数
int get_next(int key) {
    split(root, key, x, y); //按key分y最左节点是后继
    int p = y;
    while (tr[p].l) p = tr[p].l;
    int res = tr[p].key;
    root = merge(x, y);
    return res;
}

//创建FHQ Treap带哨兵的空树
void build() {
    get_node(-INF), get_node(INF);
    root = 1, tr[1].r = 2; //+inf > -inf,+inf在-inf右边
    pushup(root);          //更新root的size
}

int main() {
    //加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    //事实证明，套路很重要
    build();

    int q;
    cin >> q;
    while (q--) {
        int op, x;
        cin >> op >> x;
        if (op == 1)
            insert(x);
        else if (op == 2)
            remove(x);
        else if (op == 3)
            printf("%d\n", get_rank(x) - 1); //因为前面多了-INF哨兵,所以排名还需要减1
        else if (op == 4)
            printf("%d\n", get_key(x + 1)); //本来需要查询排名为x的，现在由于增加了一个左哨兵，就需要查询x+1位的
        else if (op == 5)
            printf("%d\n", get_prev(x));
        else if (op == 6)
            printf("%d\n", get_next(x));
    }
    return 0;
}

七、待研习

平衡树进阶博文 【模板】普通平衡树 - 洛谷 【模板】文艺平衡树 - 洛谷 AcWing 266. 超级备忘录 - AcWing题库 [NOI2005] 维护数列 - 洛谷 【模板】可持久化平衡树 - 洛谷 【模板】可持久化文艺平衡树 - 洛谷 【模板】二逼平衡树（树套树） FHQ-Treap(非旋treap/平衡树)——从入门到入坟