|
|
##[$POJ$ $3067$ $Japan$](http://poj.org/problem?id=3067)
|
|
|
|
|
|
### 一、题目大意
|
|
|
两对岸,一边$n$个点,一边$m$个点,现在连$k$条线,问有几个交点。
|
|
|
|
|
|
### 二、题目解析
|
|
|
梳理一下这其实是一个问逆序对的问题,为什么是逆序对?
|
|
|
|
|
|
举例:
|
|
|
```cpp {.line-numbers}
|
|
|
1
|
|
|
3 4 4
|
|
|
1 4
|
|
|
2 3
|
|
|
3 2
|
|
|
3 1
|
|
|
```
|
|
|
<img src='https://img-blog.csdn.net/2018073016441752?watermark/2/text/aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L05vc2NyZWFk/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70'>
|
|
|
|
|
|
依题意可得上图,算出$5$个交点,除了作图还有什么方法可以得到答案呢?
|
|
|
|
|
|
我们不妨先把$n$的元素看成是有序的,例子就是如此($1$,$2$,$3$,$3$)对应的是($4$, $3$, $2$, $1$)因为有相同的数据存在,相同位的从小到大排序($4$,$3$,$1$,$2$),如果这个结果是($1$,$2$,$3$,$4$)的话,是不是就没有交点了,因为 **没有逆序对存在**。
|
|
|
|
|
|
把逆序对互换直到为零,操作步数就是$5$,其实每添加一条线,增加的点数就是增加的逆序对数,还无法理解就按上述步骤模拟几组数据,明白要干什么。
|
|
|
|
|
|
剩下的就是非常经典的求逆序对问题了。
|
|
|
|
|
|
**步骤**:
|
|
|
- 将每条线段封装成结构体,并且,按左端点由小到大排序,如果左端点一致,则按右端点由小到大排序。(这似乎是最终无逆序时的顺序)
|
|
|
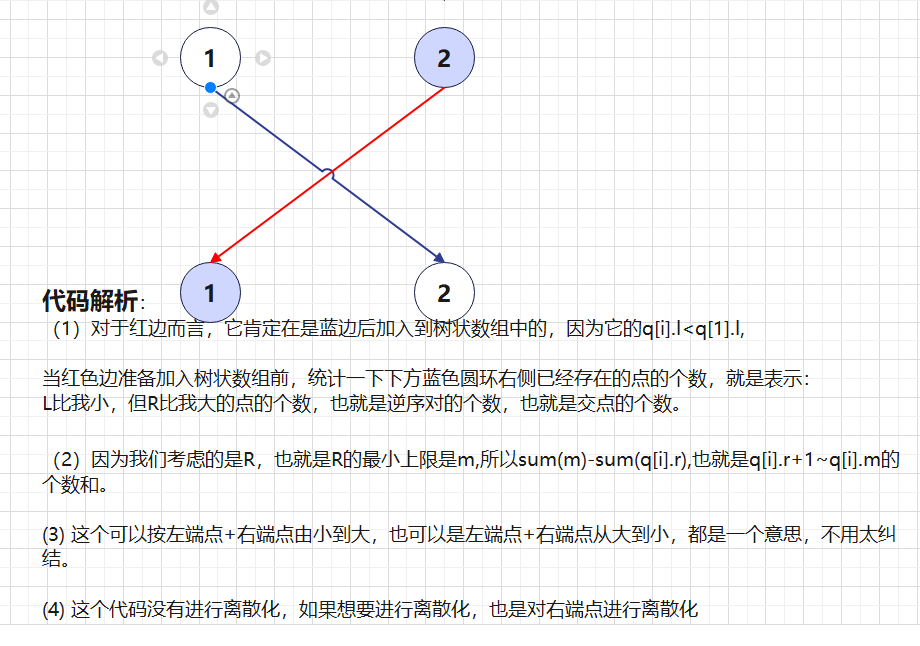
- 从小到大,逐个进入树状数组,在每条边进入时,检查是不是已经存在,左端点比自己小,或者左端点一致,但右端点比自己小的边,已经出现在了自己的右侧,这样的话,这种边就会与自己形成一个逆序。
|
|
|
|
|
|
|
|
|
|
|
|
### 由小到大排序+树状数组
|
|
|
```cpp {.line-numbers}
|
|
|
#include <cstdio>
|
|
|
#include <string.h>
|
|
|
#include <algorithm>
|
|
|
#include <iostream>
|
|
|
using namespace std;
|
|
|
typedef long long LL;
|
|
|
const int N = 1e6 + 10;
|
|
|
|
|
|
int n, m;
|
|
|
struct Node {
|
|
|
int l, r;
|
|
|
const bool operator<(const Node &t) const {
|
|
|
if (l == t.l) return r < t.r;
|
|
|
return l < t.l;
|
|
|
}
|
|
|
} q[N];
|
|
|
|
|
|
// 树状数组模板
|
|
|
#define lowbit(x) (x & -x)
|
|
|
int c[N];
|
|
|
void add(int x, int v) {
|
|
|
while (x < N) c[x] += v, x += lowbit(x);
|
|
|
}
|
|
|
LL sum(int x) {
|
|
|
LL res = 0;
|
|
|
while (x) res += c[x], x -= lowbit(x);
|
|
|
return res;
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
#ifndef ONLINE_JUDGE
|
|
|
freopen("POJ3067.in", "r", stdin);
|
|
|
#endif
|
|
|
int T;
|
|
|
scanf("%d", &T);
|
|
|
int cnt = 0;
|
|
|
|
|
|
while (T--) {
|
|
|
memset(c, 0, sizeof c);
|
|
|
int k;
|
|
|
scanf("%d %d %d", &n, &m, &k); // 左右两边分别有n和m个城市,然后k行给出连边,问共有多少交叉点
|
|
|
|
|
|
for (int i = 1; i <= k; i++) scanf("%d %d", &q[i].l, &q[i].r);
|
|
|
|
|
|
sort(q + 1, q + 1 + k); // 按左端点由小到大,右端点由小到大排序
|
|
|
// 没有离散化
|
|
|
// Q:为什么这里不使用离散化呢?为什么前一题 一维逆序对的数量就要使用离散化呢?
|
|
|
// 答:因为前一题的数值1e9,而个数是1e5,所以需要映射到1~1e5的空间上,再用二分快速找出相对位置
|
|
|
// 而本题,数值l,r 与 个数其实是一个概念,都是小于等于1000的,无需离散化。
|
|
|
|
|
|
LL res = 0;
|
|
|
for (int i = 1; i <= k; i++) { // 捋着原数组来,也就是一条边一条边来,逐个进入树状数组
|
|
|
// 当i号边进入树状数组时,在它前面进入的,肯定是左端点比自己小的,也就是值比自己小,
|
|
|
// 那么,就检查出现的位置,也就是对应的出现在自己右侧的端点个数
|
|
|
res += sum(m) - sum(q[i].r); // 注意这里的sum(m),因为考查的是右端点,而右端点的上限是m
|
|
|
add(q[i].r, 1);
|
|
|
}
|
|
|
printf("Test case %d: %lld\n", ++cnt, res);
|
|
|
}
|
|
|
return 0;
|
|
|
}
|
|
|
```
|